E-COE-1 Two masses are connected via a simple pulley. m₁ is on a horizontal surface while m₂ is on an incline. If you were trying to determine the final speed of the second mass once its traveled some distance down the incline, which of the following physics are useful in the analysis?

(Note: Draw a line to define a system boundary that would have zero non-conservative work being done in it.)

1. Kinematics
2. Newton's 2^nd Law Mechanics
3. Impulse and Momentum
4. Conservation of Energy

E-COE-2a Tarzan is in the path of a pack of stampeding elephants when Jane swings in to the rescue on a rope vine, hauling him off to safety. If the length of the vine is 25 m, and Jane starts her swing with the rope horizontal, how fast is she traveling right before picking up Tarzan?

E-COE-2b If Jane’s mass is 54 kg, and Tarzan’s is 82 kg, to what height above the ground will the pair swing after she grabs him. Answer: 3.94 m

E-COE-3a Starting from rest, two identical 2-kg masses slide down different angle frictionless inclines.

If the angle from the horizontal in the second case is 65^o and the incline is 11.03 m long, how fast will the mass be moving when it reaches the bottom of the incline?

E-COE-3b Starting from rest, the same two identical 2-kg masses slide down different angle inclines that both have identical coefficients of kinetic friction.

Which mass will have the greater final kinetic energy when reaching the bottom.
1. 1
2. 2
3. same
4. not enough information

E-COE-4 A 2-kg mass is compressed 1 m against a spring whose spring constant k is 20 N/m. Once released the mass slides down a frictionless ramp then back up to another spring with the same spring constant. After compressing the second spring it comes to rest and is held in place. Rank the work done by the normal force from the ground during the following intervals.

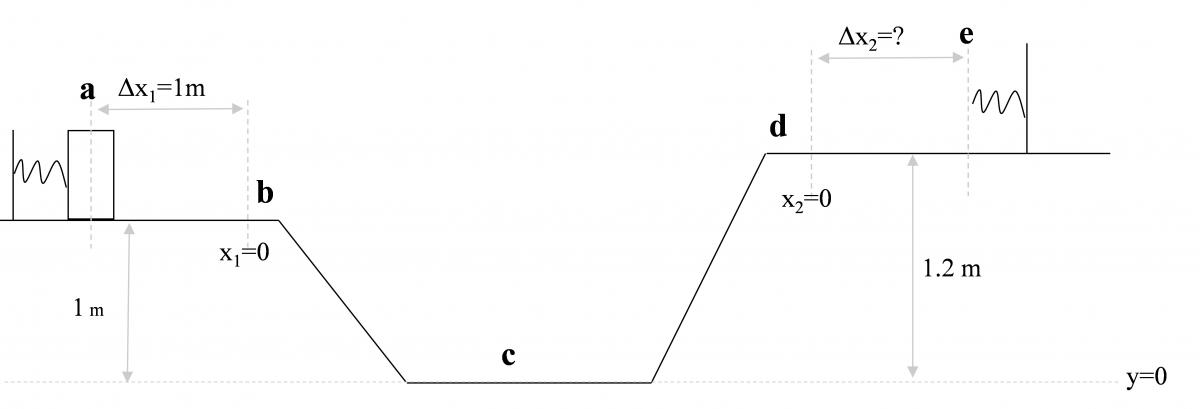
• a to b
• b to c
• c to d
• d to e

What is the speed in m/s of the mass at point c?

E-COE-5 A box of mass m starts from rest on a horizontal surface on a planet with an acceleration of gravity g. Wind applies a constant horizontal force F^w on the box. After traveling a distance d on the horizontal surface the box encounters an inclined plane that makes an angle of θ up from the horizontal. To what height h will the box reach before momentarily coming to rest? All surfaces are frictionless.