Check out the trippy effect when you put a diffraction grating over white lights! Learn how this effect happens!
Pre-lecture Study Resources
Watch the pre-lecture videos and read through the OpenStax text before doing the pre-lecture homework or attending class.
BoxSand Introduction
Wave Optics | Multi and Single-Slit Interfernce
Multi-Slit Interference
A preferred experiment to measure the wavelength of light is the multi-slit experiment. Instead of only two openings, you have multiple slits, which has the effect of sharpening the constructive interference peaks. The multi-slit apparatus is called a diffraction grating when light passes through it and a reflection grating when light reflects off of it. Below is a diagram for a diffraction grating.
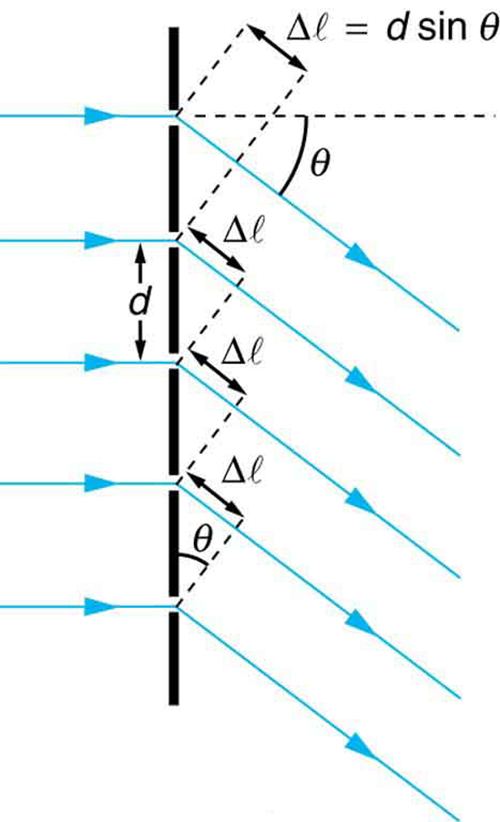
Here the first slit interferes with the second and the second with the third, and so on. Each subsequent slit has the same PLD condition as for a double slit. It is a bunch of double slits slightly shifted from each other. The result is a sharper set of interfrence fringes and the same conditions and equations as for the double slit.
Single Slit Interference
Once you have a wave picture of light and understand superposition, the inteference patterns of the double slit and muti-slit setups are not wierd. But what's truely a mind bender is when passing light through a single slit you also observe an interference pattern, although one different from the double slit. To understand this effect you must consider Huygens Principle which states that each point on a wavefront can act as a new spherical source (left figure).
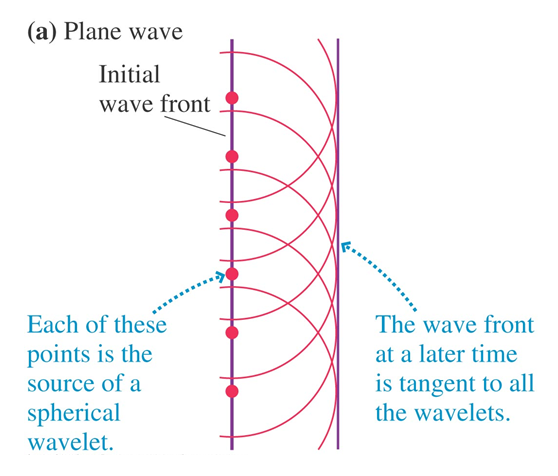
Each new spherical source interfere to create the next wavefront, which can then be a set of new spherical sources. This may seem counter intuitive and we don't know if light really behaves this way, but if modeling it this way is consistent with observation, we can't throw it out as a possibility. In fact this model then helps us understand the single slit interference pattern. Now waves generated at the top of the source can interfere with waves on the bottom of the source (figure above on the right).
The interference pattern is similar in that there are light and dark regions but it differs in the locations of the maxima and minima.
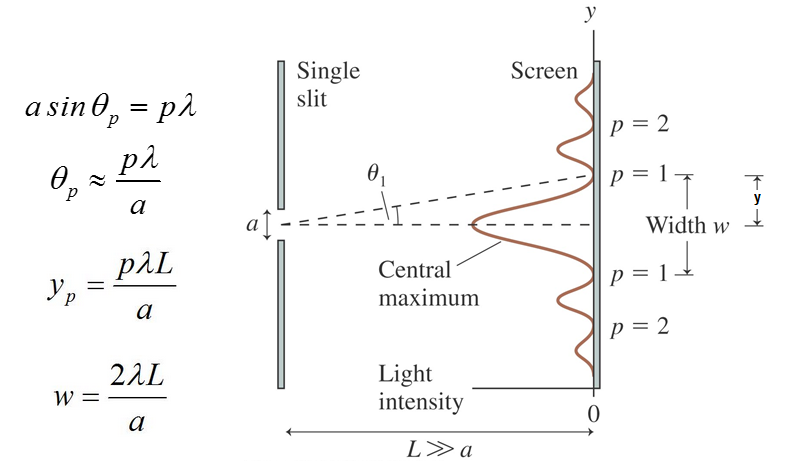
The interference is also often discribed by the locations of the destructive interference points. Here the integer $p$ is describing the order of the dark fringes. The width of the cental maximum ($w$) can be found by doubling $y_1$.
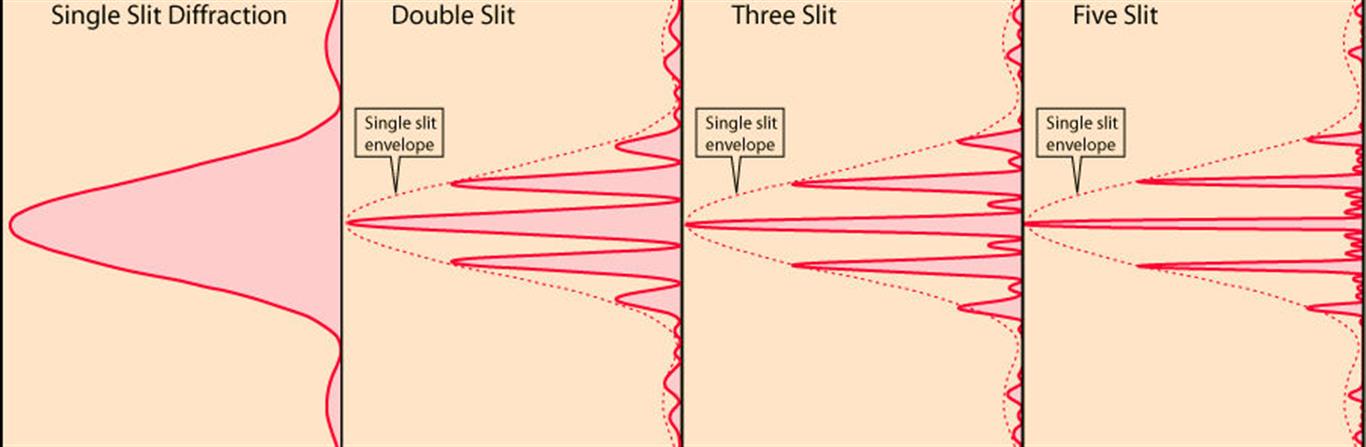
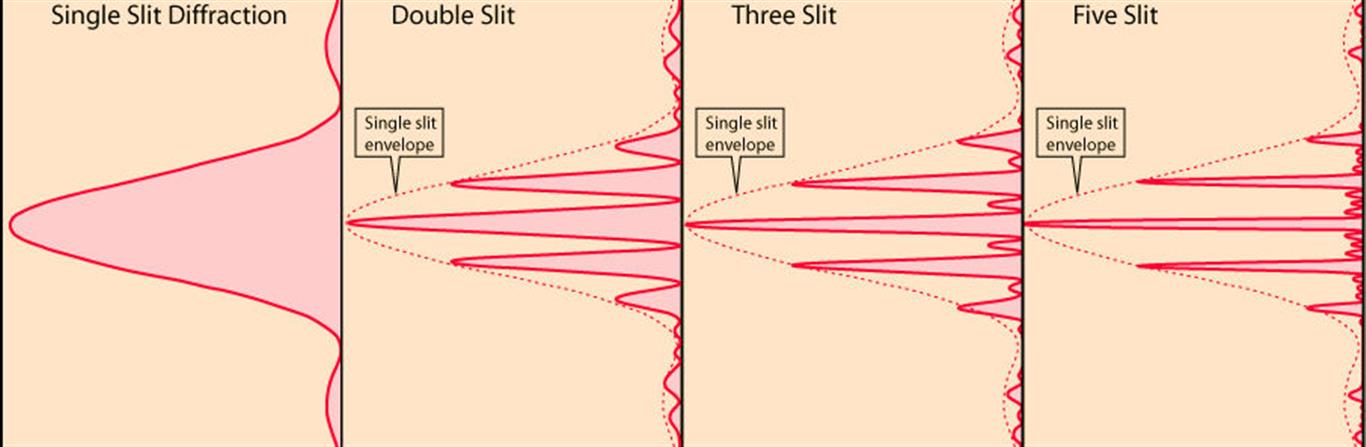
To see the difference between the single and the double slit interference patterns, along with the effects of sharpening the fringes by adding more slits, refer to the figure below.
Single-Slit Interference Mathematical Model
To explain why the mathematical model for single slit interference uses destructive interference fringes, unlike either of the double or multi-slit models, we need to consider several special cases illustrated below.
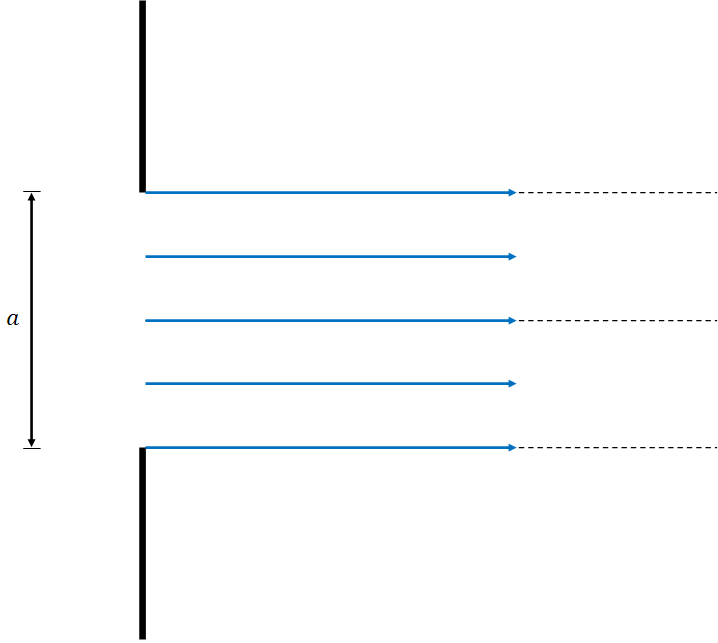
We will split the single slit into successively more equal sections. The first of which we will consider is the slit as a whole. We see that light incident on the slit can simply shine directly through the slit onto a screen opposite the slit. Since these rays are all parallel with no path length difference between them, they will interfere constructively and we will find a central bright spot on the screen directly opposite the slit.
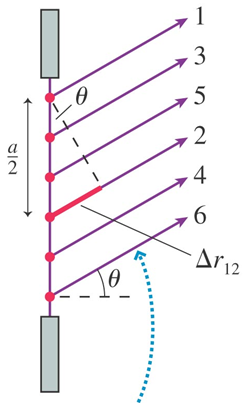
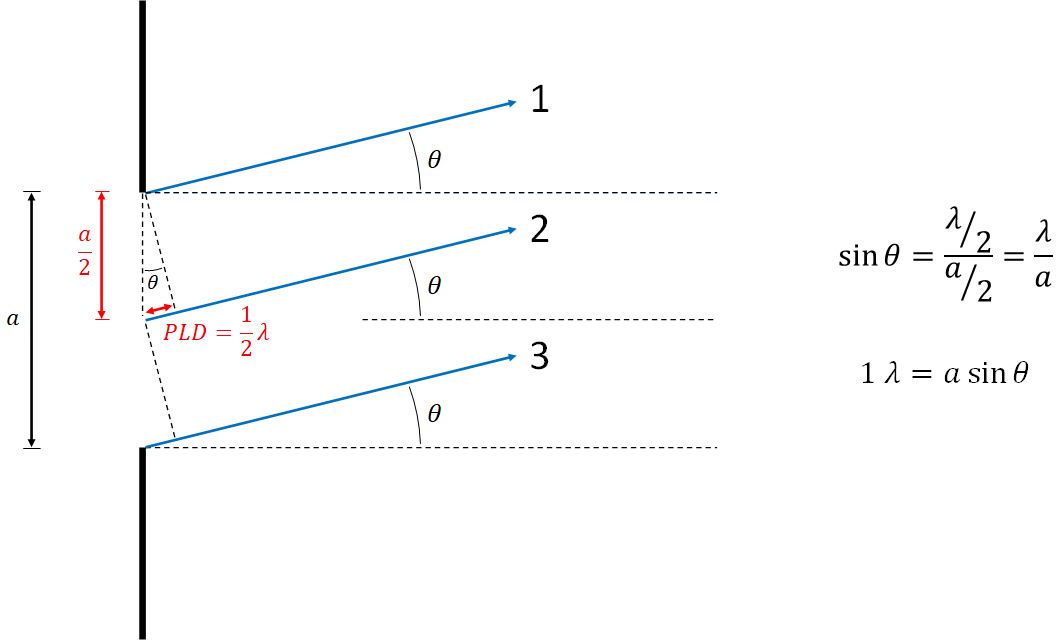
To find the angle at which the first destructive interference, dark, fringe occurs, we will divide the single slit of width a into equal sections of width a/2. Additionally, we will consider waves which have been diffracted up at a slight angle. We will examine three waves, one from the top edge of the slit (labeled with a number 1), another from the middle of the slit (labeled with a number 2), and a final wave from the bottom edge of the slit (labeled with a number 3). We will choose an angle such that there is a path length difference of one half of a wavelength between the top and middle waves. We can then examine the triangle made near the start of waves 1 and 2. The sine of the shown angle is the opposite side (1/2 lambda) divided by the hypotenuse (a/2). Simplifying this, we find the equation given between the images. The "1" before the lambda is emphasized because this will eventually be our variable labeled "p". This is the p = 1 dark fringe, which is the first fringe on either side of the central bright spot.
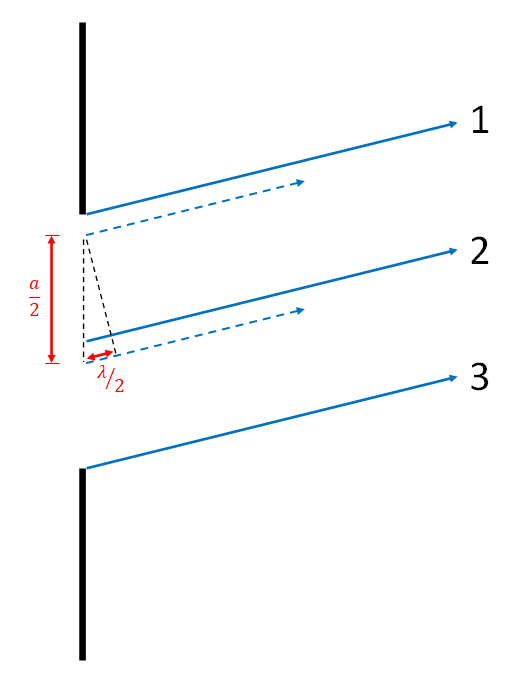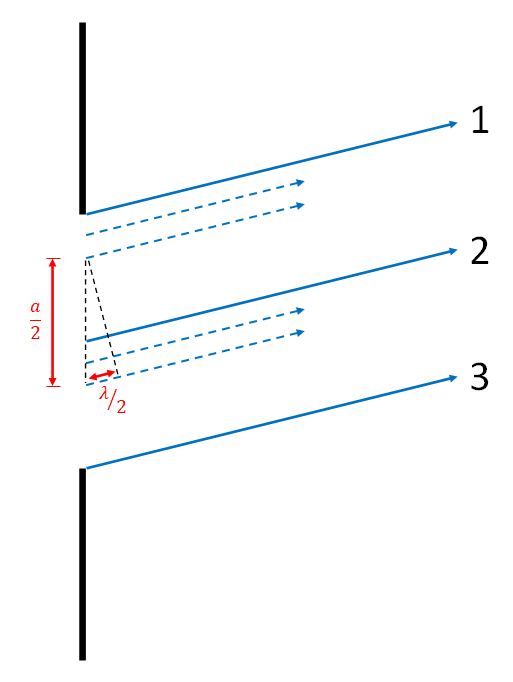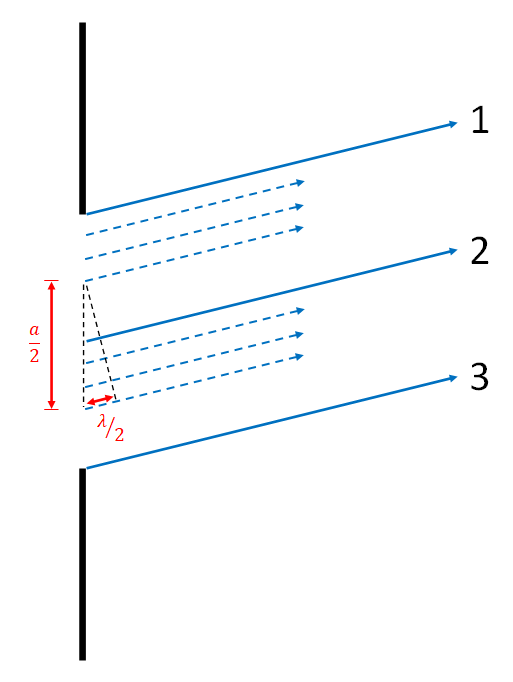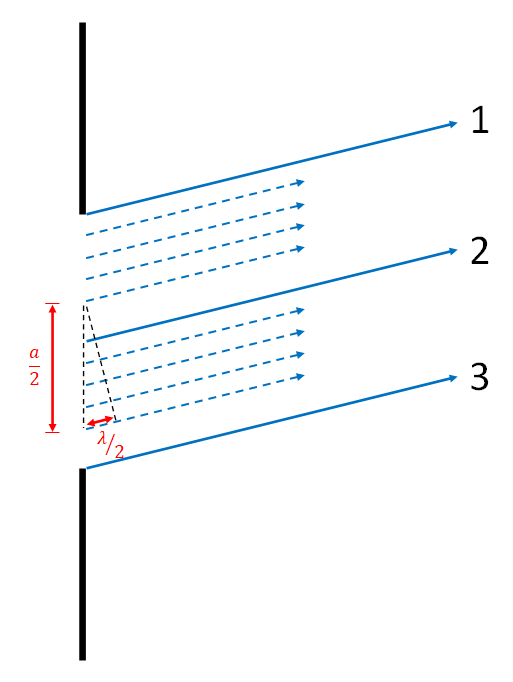
To see that this gives a destructive interference fringe, we can look at the animated gif. For every wave between waves 1 and 2, there is a corresponding wave between 2 and 3 which starts a distance a/2 away, and has a path length difference of one half of a wavelength, thus causing destructive interference.
Next we look at what happens when we divide the single slit into three equal sections of width a/3 and perform the same procedure as above. The diffraction angle needs to increase in order to give the same path length difference of lambda / 2. We find that the resulting equation might represent a "p" value of 3/2. This doesn't fit the mathematical model presented above, so this is a hint that this situation doesn't quite work out!
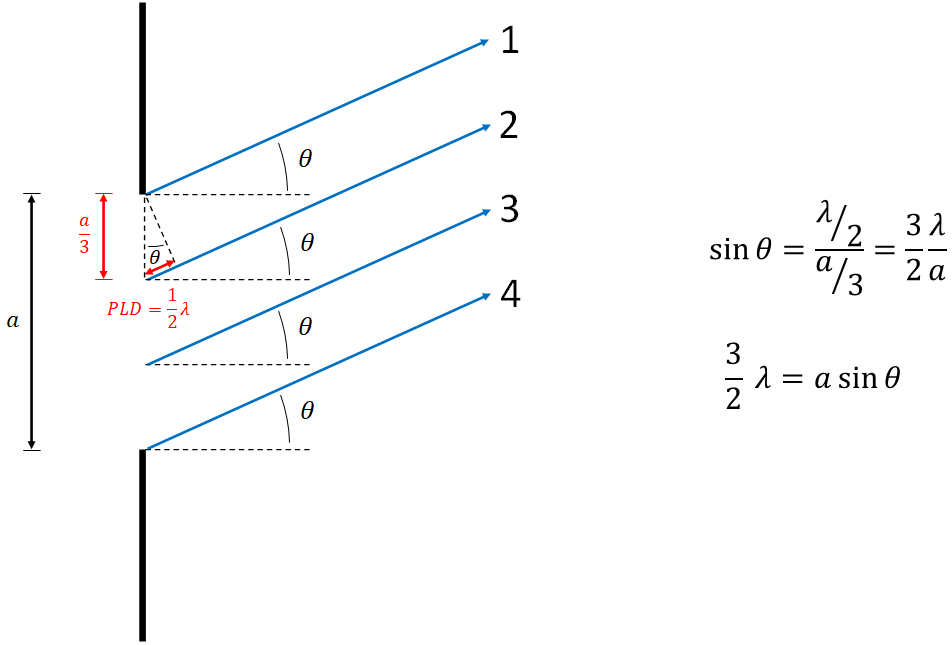
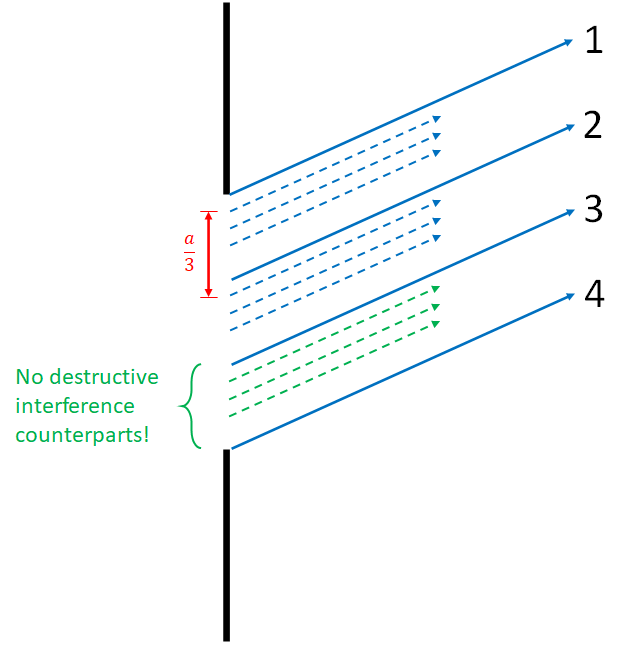
To see that this case is a little funny, look at the image on the right, which shows that as in the first case, for every wave between waves 1 and 2 there is a wave between 2 and 3 which results in destructive interference. However, there is another whole section between waves 3 and 4 which do not have corresponding destructive interference. This means that some light does get through the slit at this angle, and we do not see a destructive interference at this angle. Note that in actuality it is not just the bottom set of waves that get through, there is actually partial destructive interference all around. But that image is a useful conceptual picture to show that there is not complete destructive interference happening as there would be for a dark fringe.
Finally, we look at what happens when we divide the single slit into four equal sections of width a/4. We see that for this case, we arrive at a nicer mathematical model with a "p" value of 2. We also see, in the image on the right, that there are now two sets of two regions which each destructively interfere with each other. This results in the p = 2 dark fringe.
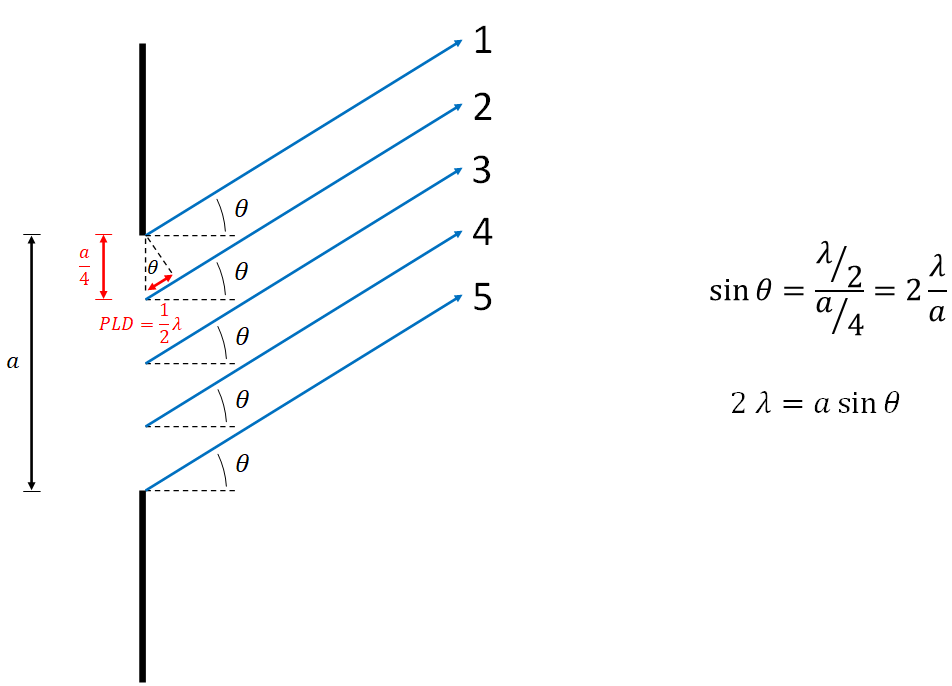
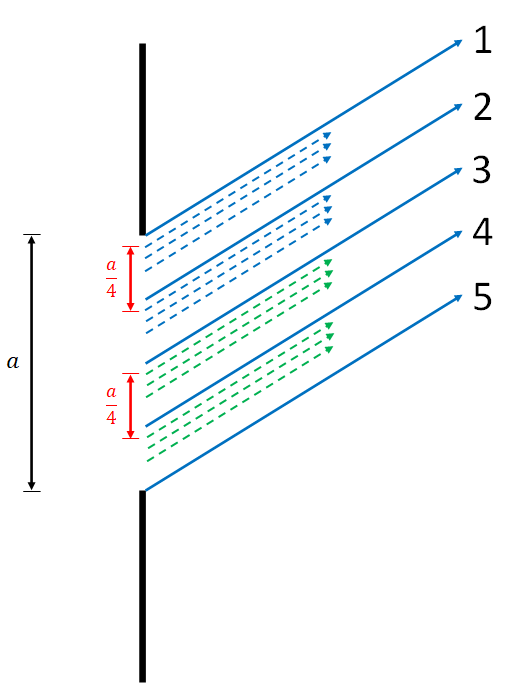
We can repeat this process to find that the p = 3 case will come from dividing the single slit into 6 even sections. From here we can generalize this process to describe the angle of dark fringes from a single slit. We find that the mathematical model is p lambda = a sin(theta), where p = 1, 2, 3, etc. Note that p starts at 1, where m started at 0 for the double and multi-slit mathematical model. The single slit mathematical model also finds the locations of the dark fringes.
Key Equations and Infographics






Now, take a look at the pre-lecture reading and videos below.
BoxSand Videos
Required Videos
Diffraction and Reflection Gratings
Diffraction Grating - conceptual (6min)
Reflection Grating - conceptual (4min)
Single Slit Interference
Single Slit Diffraction (11min)
Single Slit Diffraction - equations(4min)
Spectroscopy and Crystallography
Suggested Supplemental Videos
OpenStax Reading
Fundamental examples
(1) A red laser with wavelength $\lambda = 700$ nm shined on a double-slit with width $d=10$ mm. The screen is located $D= 2 $ m away from the slit. How far up from the central maximum is the $m=2$ bright fringe?
(2) How does the position of the 2nd bright fringe in example 1 change if the wavelength used is $\lambda_{new} = 350$ nm instead of $\lambda_{old} = 700 $ nm?
(3) In a single-slit experiment, the width of the central maximum is $1.5 $ mm. The screen is 1 meter from the slit and the wavelength of light used in this experiment is $360 $ nm. (a) What is the size of the slit? (b) How much wider would the central maximum be if the wavelength was tripled?
(4) In a single-slit experiment, the second dark fringe is located 7.5 cm from the center of the central maximum on a screen located $L = 3 m$ away from the slit. What is the distance between the second dark fringe and the third dark fringe that is located on the other side of the central maximum? The wavelength of the illuminating light is $\lambda = 600 $ nm.
Solutions found HERE
Short foundation building questions, often used as clicker questions, can be found in the clicker questions repository for this subject.
Post-Lecture Study Resources
Use the supplemental resources below to support your post-lecture study.
Practice Problems
Conceptual Problems
BoxSand's multiple select problems
BoxSand's quantitative problems
Recommended example practice problems
- PhysLabs
- Double Slit Worksheet: Website Link
- Single Slit Worksheet: Website Link
- OpenStax Practice problems at the end of sections
- Young's Double Slit: Website Link
- Multiple Slit Diffraction: Website Link
- Single Slit Diffraction: Website Link
For additional practice problems and worked examples, visit the link below. If you've found example problems that you've used please help us out and submit them to the student contributed content section.
Additional Boxsand Study Resources
Additional BoxSand Study Resources
Learning Objectives
Summary
Summary
Atomistic Goals
Students will be able to...
YouTube Videos
Doc Schuster covers wave interference,
Doc Shuster covers single slit diffraction,
Some mathematics behind double slit diffraction,
Simulations
Phet - wave interference,
For additional simulations on this subject, visit the simulations repository.
Demos
History
Oh no, we haven't been able to write up a history overview for this topic. If you'd like to contribute, contact the director of BoxSand, KC Walsh (walshke@oregonstate.edu).
Physics Fun
Other Resources
Problem Solving Guide
Use the Tips and Tricks below to support your post-lecture study.
Assumptions
Checklist
1. Read the problem carefully and visualize the physical setup.
2. Determine if it is indeed a problem best analyzed with wave optics and not ray optics.
3. Determine what physical model best fits the problem. Is it a double, multi, or single slit interference or is a thin film effect?
4. For the type of system, draw the appropriate physical representation.
5. Organize the relevant equations for the specific system.
6. Determine what variables are known or unknown. Perhaps what variables are changing - is it a proportional reasoning problem?
7. If it is a slit problem, is it in the small angle approximation? If so, how does this simplify the equations?
8. Solve the system of equations, perhaps with the use of geometry (this is a big step and mastery comes with practice).
9. Check your answer for reasonableness. Magnitude, dimensions, limiting cases?
Misconceptions & Mistakes
- ... students mistakenly assume all the interference patterns are the same
- ... students mistakenly make the small angle approximation for all cases
- ... students mistakenly ignore the $\pi$ phase shifts in certain reflections in a thin film interference
Pro Tips
- Draw the physical representation - being able to see the fringes and the geometry is very useful
Multiple Representations
Multiple Representations is the concept that a physical phenomena can be expressed in different ways.
Physical
The diagram for Young's double slit experiment depicts the important features used to describe the phenomena.
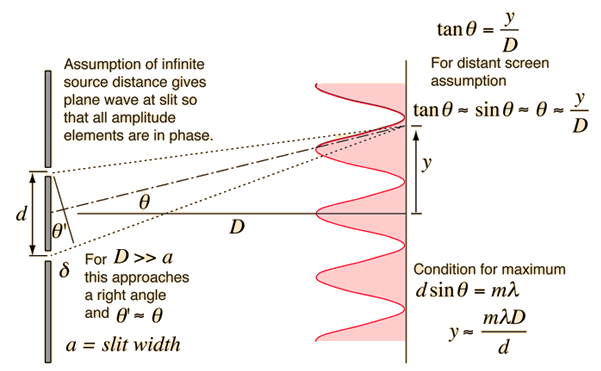
From a single slit diffraction to mutli slit diffraction the single slit forms an envelope where the sharpness of bright peaks become more sharp as the number of slits is increased.
Mathematical






Graphical
Descriptive
Experimental