All charged objects produce a thing we call their electric field. It is not observable in the conventional sense and might be thought of as a clever way to keep track of how charged objects interact. The field from one electron can influence another electron and the result is they feel a repelling force. 

Large electric fields are in the atmosphere during storms.

https://www.youtube.com/watch?v=SglzRDD1oNI

Pre-lecture Study Resources

Watch the pre-lecture videos and read through the OpenStax text before doing the pre-lecture homework or attending class.

BoxSand Videos

Learning Objectives

Summary

Summary

Atomistic Goals

Students will be able to...

  1.  

BoxSand Introduction

Electric Fields  |  Point Charges


Point Charge

The electric field for a point charges points away from positive charges and towards negative charges. It's magnitude has an inverse square dependency on the distance from the charge. If you double your distance from the charge the field decreases by a factor of 4. All of this information is contained in the expression below.

Electric Field for a Point Charge

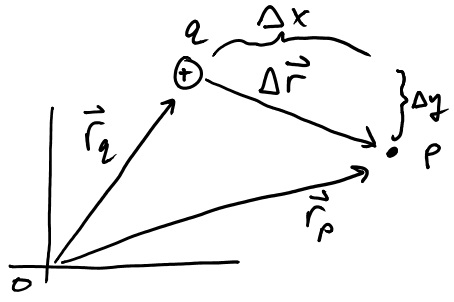This is a physical representation of an electric field for a point charge. There is a positively charged ion at some distance from the origin labeled as r q and there is another point p from the origin labeled as r p. The distance between the charged ion and point p is delta r where there is a change in x and y position.                     $\overrightarrow{E}_q(\overrightarrow{r}_p) = \frac{kq}{|\Delta \overrightarrow{r}|^2}\Delta \hat{r}$ 

The above equation reads that the electric field from charge $q$, at point $p$, is equal to a constant ($k=8.99 x 10^9 N m^2/C^2$) times the charge, divided by the square of the absolute value of the change in position from $q$ to $p$, multipled by the delta $r$ hat direction. The $\Delta \hat{r}$ is a unit vector, meaning it has magnitude of 1 and only provides a direction.

$\Delta \overrightarrow{r} = <\Delta{x}, \Delta{y}, \Delta{z}>$

$\Delta \hat{r} = < \frac{\Delta x}{|\Delta \overrightarrow{r}|}, \frac{\Delta y}{|\Delta \overrightarrow{r}|}, \frac{\Delta z}{|\Delta \overrightarrow{r}|}>$

Key Equations and Infographics

A representation with the words electric field for a point charge on the top. There is an equation that shows that the electric field from charge q, at point p, is equal to the Coulomb’s constant multiplied by the charge divided by the square of the change in position vector pointing from q to p, multiplied by the delta r hat direction. This is also written in words below.

 

A representation with the words net electric field on the top. There is an equation that shows that the net electric field is equal to the summation of each electric field vector. This is also written in words below.

 

A representation with the words the electric field due to an infinite sheet on the top. There is an equation that shows that the magnitude of the net electric field is equal to the total charge divided by two times the electric constant multiplied by the area of the sheet. This is also written in words below.

Now, take a look at the pre-lecture reading and videos below.

OpenStax Reading


OpenStax Section 18.5  |  Electric Field Lines: Multiple Charges

Openstax College Textbook Icon

 

Equations, definitions, and notation icon Concept Map Icon
Key Terms Icon Student Contributed Content Icon

Additional Study Resources

YouTube Videos

 

Pre-Med Academy has a lot of videos about the Electric Field and Force, too many to list here. We really recommend checking out the content repository for this section and check out the rest of their videos Here are just a few on The Electric Field, Electric Field of a Point Charge, and Electric Field of an Infinite Wire.

Youtube: Pre-Med Academy - Electric Field

Youtube: Pre-Med Academy - Electric Field of a Point Charge

 

Doc Schuster has a few good videos on the Electric field. 

 

Youtube: Doc Schuster - The Electric Field

 

Youtube: Doc Schuster - How to Draw and Interpret Field Lines

 

Youtube: Doc Schuster - Conductors in Electrostatic Equilibrium, Rules for Electric Fields

 

Other Resources

This link will take you to the repository of other content related resources .

Content Icon

Simulations


 

This flashphysics applet lets you create charge distributions from point charges and plot the corresponding electric field.  Try placing test charges in the region of space to watch possible trajectories!

LINK THAT NEED IMAGE

This PhET interactive is a test of skill! place charges to guide a charged hockey puck around obstacles and into the goal

Phet Interactive Simulations Icon

This Puzzle by Duffy will help you connect the charge and the field.

B.U. Physics Icon

The Puzzle by Duffy is a bit more challenging.

B.U. Physics Icon

Use this 3D applet by Falstad to visualize the field for various charge distributions.

Simulation Icon

For additional simulations on this subject, visit the simulations repository.

Simulation Icon

Demos


For additional demos involving this subject, visit the demo repository

Demos Icon

History


Oh no, we haven't been able to write up a history overview for this topic. If you'd like to contribute, contact the director of BoxSand, KC Walsh (walshke@oregonstate.edu).

Physics Fun

 

Other Resources


Use the supplemental resources below to support your post-lecture study.

Boston University's Page on electric Field is a neat reference with a couple of example problems

B.U. Physics Icon

PPLATO is a complete resource with a lot of information, and several practice questions per subject. This webpage covers electric charge, the electric field, and electric potential, we've already covered charge, so focus on the electric field, we'll get to electric potential in the next section.

Other Content Icon

Here's a link to Hyperphysics' reference for electric fields

 

Hyper Physics Icon

 

The Physics Classroom's section on electric fields. 

 

The Physics Classroom Icon

 

Isaac Physics' section on the electric field is a good short resource on the electric field. On this page there are two drop down sections on electric potential, we'll get to those in the next section, so have a look at the Electric Field, Visualizing and adding electric fields and Electric Fields in Conductors sections

 

Other Content Icon

 

Other Resources

This link will take you to the repository of other content related resources .

Content Icon

Problem Solving Guide

Use the Tips and Tricks below to support your post-lecture study.

Assumptions

 

Checklist

 

Misconceptions & Mistakes

 

Pro Tips

 

Multiple Representations

Multiple Representations is the concept that a physical phenomena can be expressed in different ways.

Physical

Physical Representations describes the physical phenomena of the situation in a visual way.

 

Mathematical

Mathematical Representation uses equation(s) to describe and analyze the situation.

A representation with the words electric field for a point charge on the top. There is an equation that shows that the electric field from charge q, at point p, is equal to the Coulomb’s constant multiplied by the charge divided by the square of the change in position vector pointing from q to p, multiplied by the delta r hat direction. This is also written in words below.

 

A representation with the words net electric field on the top. There is an equation that shows that the net electric field is equal to the summation of each electric field vector. This is also written in words below.

 

A representation with the words the electric field due to an infinite sheet on the top. There is an equation that shows that the magnitude of the net electric field is equal to the total charge divided by two times the electric constant multiplied by the area of the sheet. This is also written in words below.

Graphical

Graphical Representation describes the situation through use of plots and graphs.

 

Descriptive

Descriptive Representation describes the physical phenomena with words and annotations.

 

Experimental

Experimental Representation examines a physical phenomena through observations and data measurement.

 

Practice

Use the practice problem sets below to strengthen your knowledge of this topic.

Fundamental examples

(1) What is the magnitude of the Electric field at a location $r = 2 \hspace{0.2 cm} nm$ from a point charge with charge $q=10 \hspace{0.2 cm}nC$ that is located at the origin?

(2) Three point charges $q_1 = q_2 = q_3 = 5 \hspace{0.2 cm}nC$ are placed equidistant from each other on the x-axis: $q_1$ is located at $x= -2 \hspace{0.2 cm}nm$, $q_2$ is located at the origin, and $q_3$ is located at $x = 2 \hspace{0.2 cm} nm$. A point charge $q_4 = 1\hspace{0.2 cm} nC$ is placed on the y-axis, 2 namometers up from the origin. (a) What is the magnitude of the electric force that $q_4$ feels? (b) What is the direction of the electric force on $q_4$? (c) What is the direction of the electric force if $q_4 = -1 \hspace{0.2 cm}nC$ instead?

(3) A point charge $q_1 = -20 \hspace{0.2 cm}nC$ is located at a position $r_1 = <-3,0> \hspace{0.2 cm}nm$. (a) What is the magnitude of the electric field at point $r_a = <0, 3> \hspace{0.2 cm}nm$. (b) By what factor does the magnitude of the electric field at point $r_a$ decrease if another point charge with magnitude $q_2 = 20 \hspace{0.2 cm}nC$ is placed at the origin? (c) Calculate the magnitude and direction of the force that a point charge with magnitude $q_3 = -1 \hspace{0.2 cm}nC$ would feel if it were placed at position $r_a$ for both cases (a) and (b). [Optional (d) What is the electric force on $q_3$ if charge $q_1$ is removed?]

(4) (More time-consuming - practice with computing the electric field from multiple source charges in an arbitrary configuration) Three point charges $q_1 = 5 \hspace{0.2 cm}nC$, $q_2 = 10 \hspace{0.2 cm}nC$, and $q_3 = -2 \hspace{0.2 cm}nC$ are placed as follows: $q_1$ is located at $r_1 = <- 3,0> \hspace{0.2 cm}nm$, $q_2$ is located at $r_2 = <0,0> \hspace{0.2 cm}nm$, and $q_3$ is located at $r_3 = <1, 2> \hspace{0.2 cm}nm$. (a) What is the magnitude and direction of the electric field at point $r_p = <8, 8> \hspace{0.2 cm}nm? 

 

Solutions found HERE

Short foundation building questions, often used as clicker questions, can be found in the clicker questions repository for this subject.

Clicker Questions Icon

 

Practice Problems

BoxSand practice problems - Answers

BoxSand's multiple select problems

BoxSand's quantitative problems

Recommended example practice problems 

  • *OpenStax, has practice problems at the end of every section
  • PhysicsClassroom, 27 problems on charge and the electric field, Website Link
  • University of Greenbay: Guided problem on the electric force, Website Link

For additional practice problems and worked examples, visit the link below. If you've found example problems that you've used please help us out and submit them to the student contributed content section.

Example Problems Icon