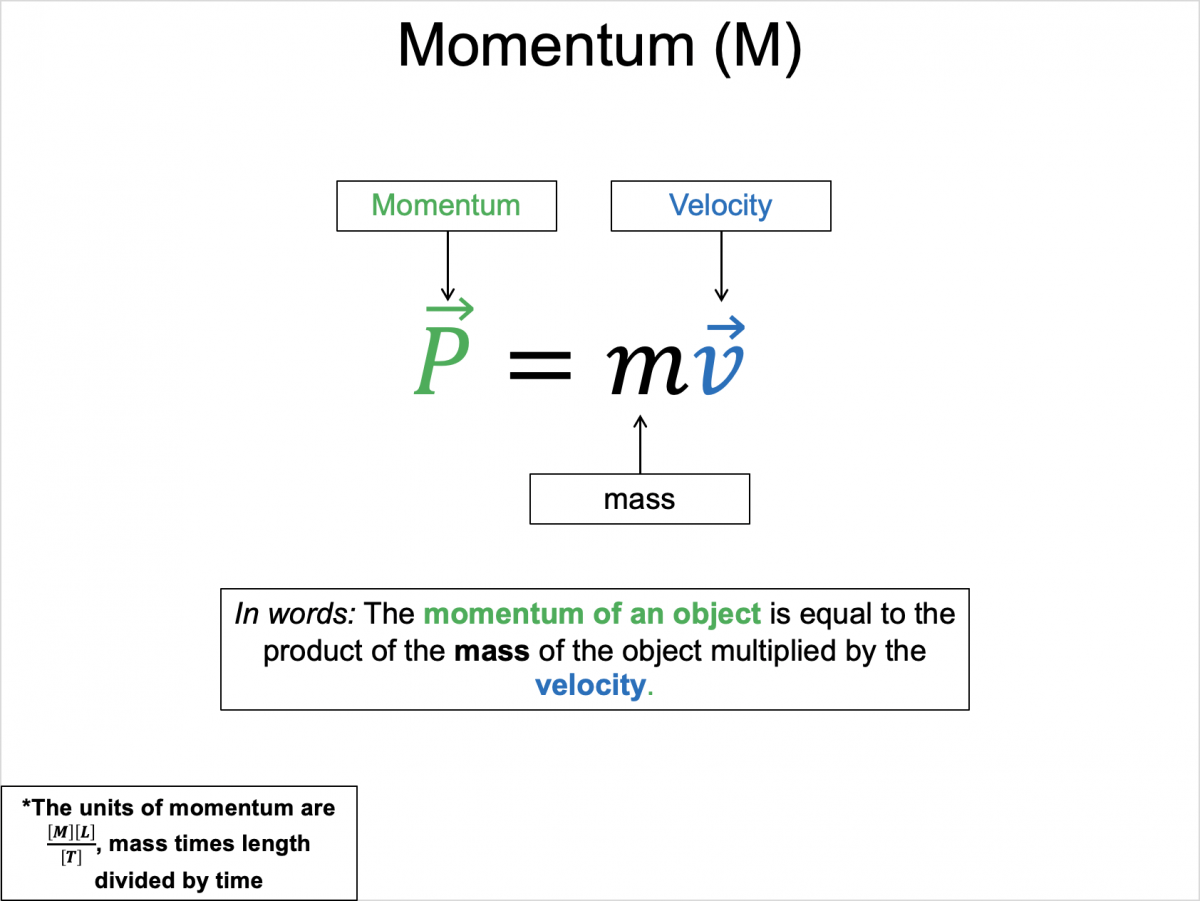
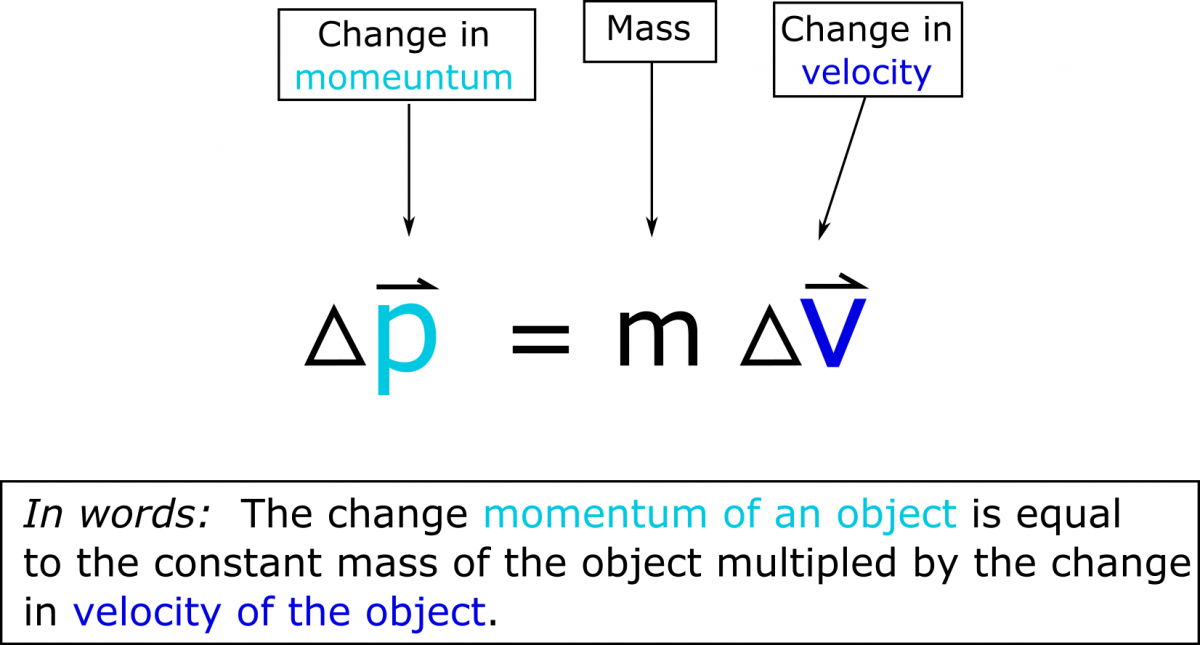
Momentum is equal to the mass multiplied by the velocity: $\vec{p} = m\vec{v}$. The SI units for momentum are kilogram meters per second (kg*m/s). Momentum can be used to determine both the direction and speed of colliding objects.
Check out this short video about the Momentum.
Pre-lecture Study Resources
Read the BoxSand Introduction and watch the pre-lecture videos before doing the pre-lecture homework or attending class. If you have time, or would like more preparation, please read the OpenStax textbook and/or try the fundamental examples provided below.
BoxSand Introduction
Momentum | Impulse
Momentum
There is a big difference between a bicycle traveling at 15 mph and a fire truck traveling with the same speed. The truck would be of more interest as it would be much harder to stop. The quantity that scales the velocity of an object by it's mass is called momentum.
$\vec{p} = m \vec{v}$
This realationship allows for small objects moving quickly to have the same momentum as large objects moving slowly. Also notice that momentum is a vector quantity because velocity is a vector quantity. Momentum and velocity must point in the same direction because they are connected by mass, a scalar.
If you are to change the momentum of a system you are going to either change its direction, or magnitude, or a combination of both. An example might be hitting a softball that is lobbed towards you. The velocity of the ball, and thus momentum right before the ball is hit is directed down an angle $\theta$ from the horizontal. After the hit, the velocity (and thus momentum) is increased and has changed directions, angled $\phi$ up from the horizontal in almost the opposite direction. A vector operation diagram describing the change in momentum (Impulse), is below.
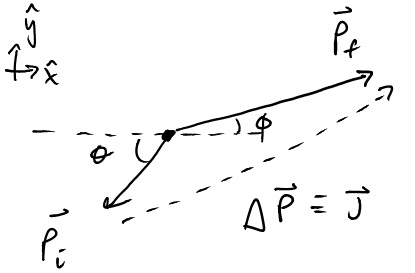
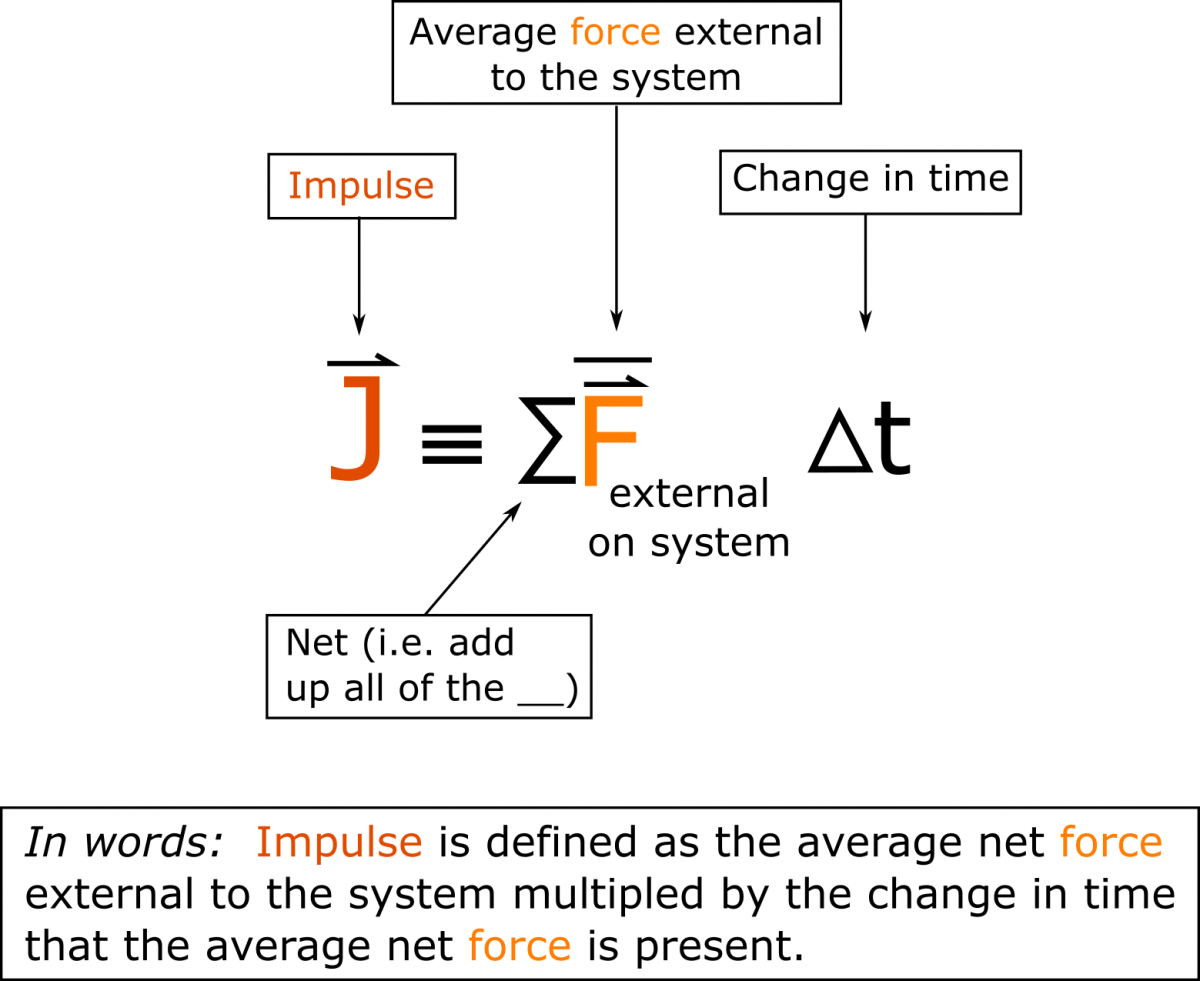
The Impulse-Momentum Theorem states that the change in momentum (impulse) of a system is equal to the average net external force acting on the system multiplied by the change in time the force was applied.
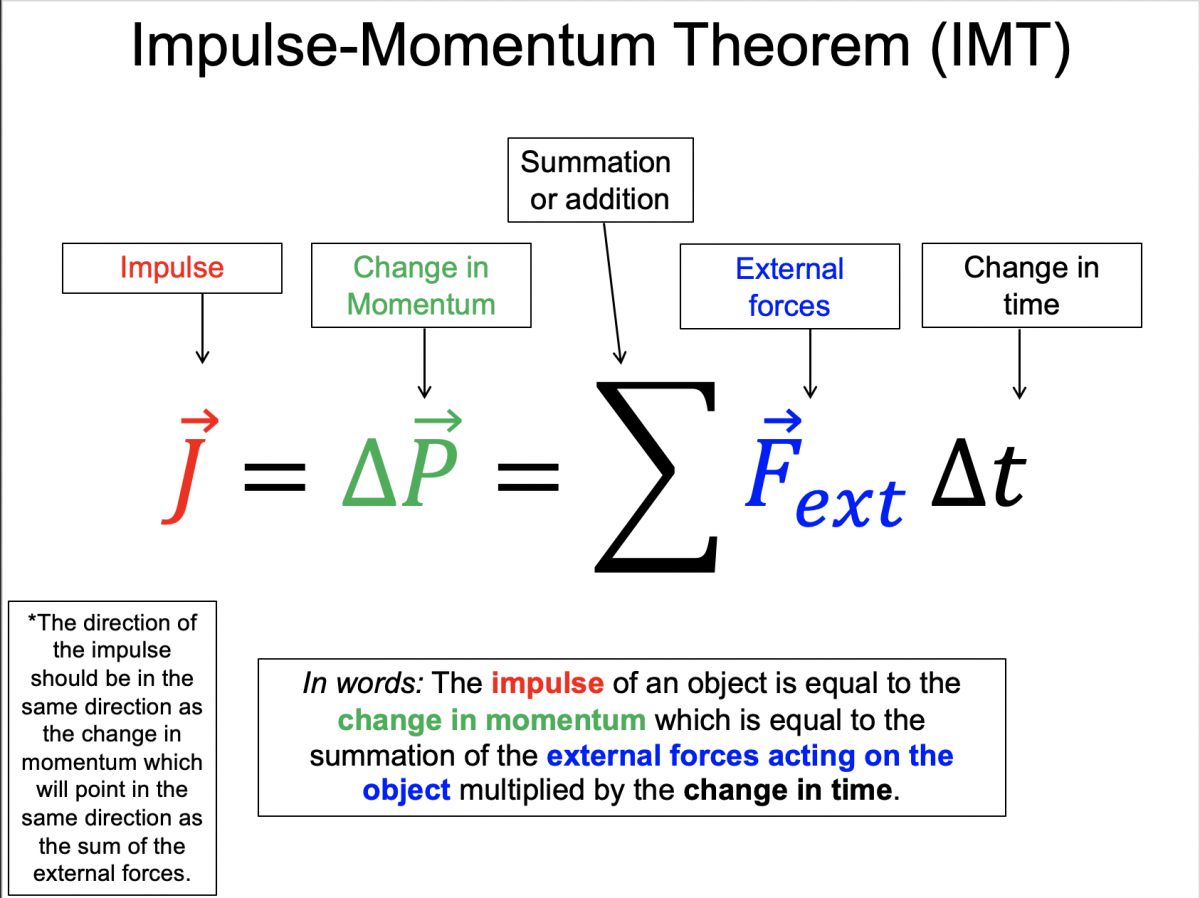
$\vec{J}=\Delta{}\vec{p} = \Sigma{}\overline{\vec{F}}_{external}\Delta t$
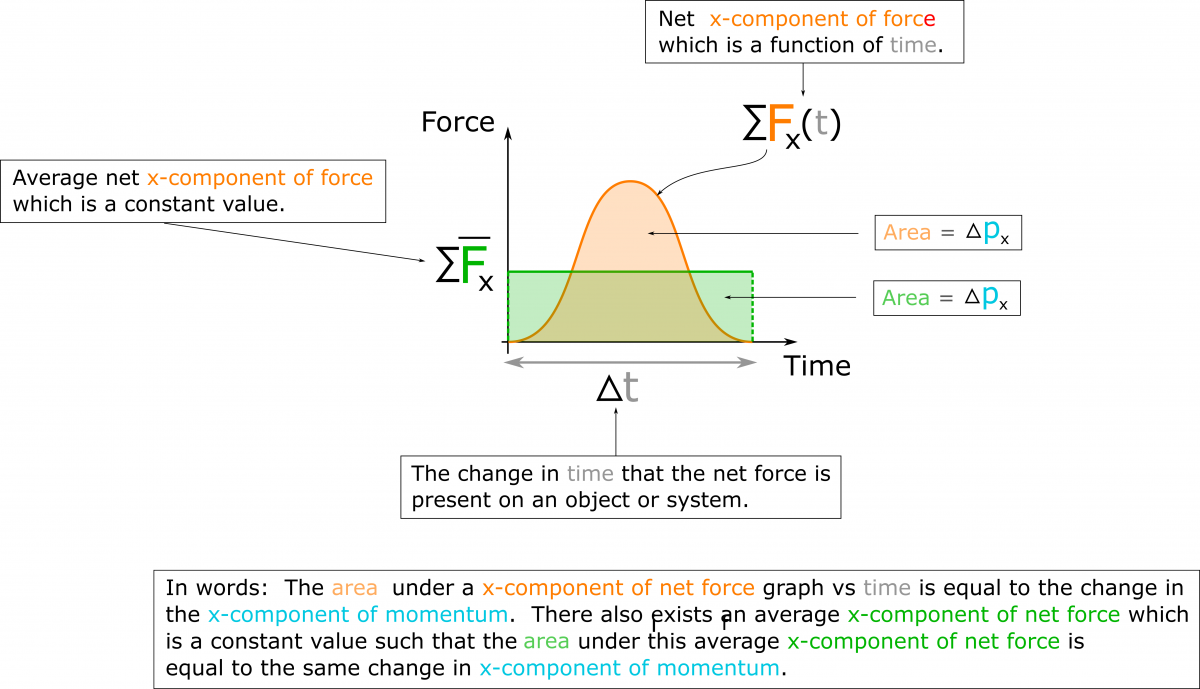
In 1D, the graphical representation of the change in momentum (impulse) is equal to the area under a net force as a function of time curve. In 2 and 3D, each component of the change in momentum is equal to the area under the force component in that direction as function of time curve. An example could be the softball that was hit by a bat. The ball (and bat to some degree) deform when they collide. As they compress, the normal force between them increases. A plot of the more realistic x-force component as a function of time is shown below.
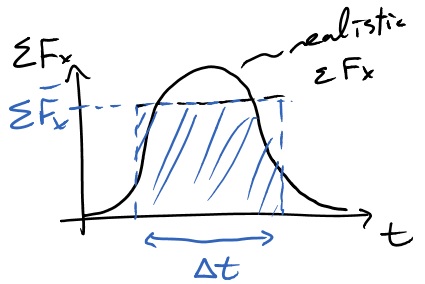
The area under that curve is the impulse imparted to the ball in the x-direction. Sometimes it is modeled more simplistically with an average constant force as a function of time. If both curves have the same area then both will have imparted equal impulse to the ball.
Key Equations and Infographics
Now, take a look at the pre-lecture reading and videos below.
BoxSand Videos
Required Videos
Suggested Supplemental Videos
OpenStax Reading
Fundamental examples
Short foundation building questions, often used as clicker questions, can be found in the clicker questions repository for this subject.
1. A pitcher throws a baseball $45 \, m/s$ horizontal to the level ground towards a batter standing at the home plate. After the batter hits the ball, the ball then travels back towards the pitcher with a speed of $55 \, m/s$ at an angle of $30^{\circ}$ from the horizontal. What is the change in momentum of the baseball?
2. A $32 \, kg$ hammer is moving at a speed of $61 \, m/s$. How large of a force is needed to stop the hammer in a time of $0.5 \, ms$?
3. The mass of a tennis ball is approximately $58 \, kg$. Sam Groth is credited for one of the fastest tennis serves at a speed of $73.18 \, m/s$ (163.7 mph!). Assume the tennis ball was initially at rest before the serve. What impulse did Sam exert on the ball during this serve if he hit the ball horizontally?
4. The image below shows a net force acting horizontally on a $3 \, kg$ object over a given amount of time. What is the final velocity of the object?
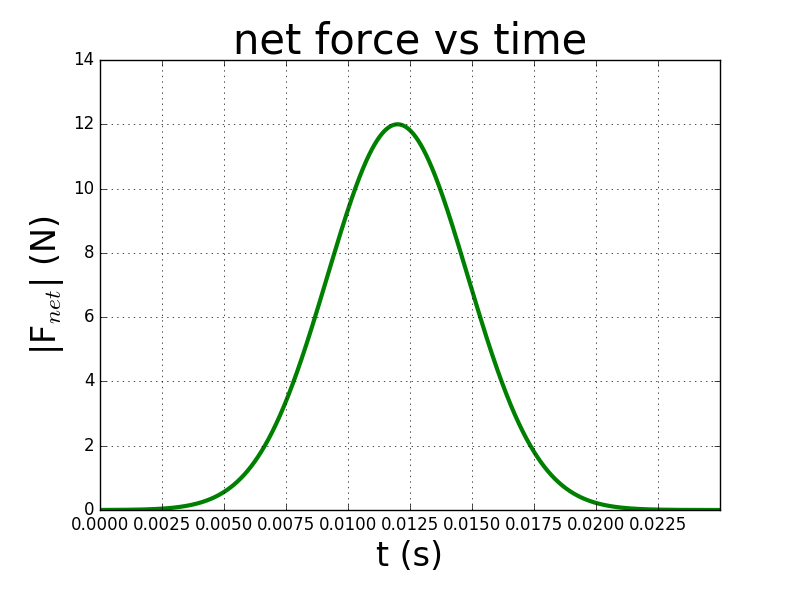
CLICK HERE for solutions.
Post-Lecture Study Resources
Use the supplemental resources below to support your post-lecture study.
Practice Problems
Recommended example practice problems
BoxSand's Quantitative Practice Problems
BoxSand's Multiple Select Problems
- BoxSand Practice Problems
- Openstax has practice problems toward the end of each section, Website Link
- Physics Tutorials with 4 short problems on impulse, Website Link
- Albert.io has a 25 question quiz on impulse, Skip questions involving energy towards the end, Website Link
For additional practice problems and worked examples, visit the link below. If you've found example problems that you've used please help us out and submit them to the student contributed content section.
Additional Boxsand Study Resources
Additional BoxSand Study Resources
Learning Objectives
Summary
The concepts of momentum and impulse are addressed. The focus is on how the impulse is equal to a change in momentum which can be determined either by direct knowledge of the initial and final momentum states or by knowing the net force applied over time.
Atomistic Goals
Students will be able to...
- Determine the magnitude of the momentum for various objects.
- Conclude that momentum is a vector because it is the product of a vector and a scalar.
- Determine the momentum of a system including multiple objects.
- Demonstrate it is harder to stop an object with larger momentum.
- Recognize that the impulse-momentum theorem can be derived from Newton's 2nd and 3rd laws.
- Define impulse as the change in momentum or equivalently as the average net force multiplied by the time elapsed during the interaction.
- Determine the change in momentum using the appropriate vector operation diagram.
- Determine the change in momentum using the mathematic representation.
- Show that impulse is equal to the area under a net force as a function of time curve.
- Identify that for a system with two objects where the net external force is zero, the impulse on one is equal and opposite of other because of
- Newton's 3rd law, and thus the net impulse of the system is zero.
- Recognize that impulse, change in momentum, net force, acceleration, and change in velocity are all vectors that point in the same direction.
- Use Newton's 3rd law to show that the contribution of the impulse from one object is negative the impulse from another object during the interaction between the two.
YouTube Videos
Khan Academy impulse and momentum dodgeball example.
How to solve Impulse momentum problems using a Force vs Time graph by Khan Academy.
Flipping Physics uses impulse to reason why you want to bend your knees when landing from a jump.
Bozeman science's lecture about Impulse, which includes a nice real-world, worked example,
Mike Spalding on youtube walks us through a basic impulse problem.
Simulations
This PhET simulation doesn't show force as a function of time but does allow you to see the net momentum vectors and the change in momentum.
For additional simulations on this subject, visit the simulations repository.
Below are instructions for the PhET:
- Click on the upper right corner to display Momenta Diagram- useful for understanding the PhET.
For additional simulations on this subject, visit the simulations repository.
Demos
This fun demo involves throwing eggs into bedsheets and not breaking them.
For additional demos involving this subject, visit the demo repository
History
Oh no, we haven't been able to write up a history overview for this topic. If you'd like to contribute, contact the director of BoxSand, KC Walsh (walshke@oregonstate.edu).
Physics Fun
Other Resources
The Physics Classroom discusses the connection between impulse, momentum, and forces.
Hyperphysics's short reference on impulse.
This page from Eastern Illinois University is very concise in its explanation of the graphical connection to impulse.
Resource Repository
This link will take you to the repository of other content on this topic.
Problem Solving Guide
Use the Tips and Tricks below to support your post-lecture study.
Assumptions
Remember the definition of Impulse $ \vec{J} = \Delta \vec{P} = \sum \vec{F}_{ext} \Delta t $, this means that if we can assume either the external force applied OR the time is very, very small, we can approximate the impulse as 0. This can sometimes be an assumption you have to make based on the physical situation, but more often it can be communitcated in the wording of problems like "a very small force" or "a force is applied instantaneously" that should ping your physics senses to justify that the force or change in time are small enough to call the Impulse 0. This will also be implied in nearly every problem in the Conservation of Momentum lectures coming up next.
Checklist
Problems with no explicit graphical representation required.
1. Draw a simple picture of both the initial and final states of the system. Use vectors to describe the initial and final velocity or momentum.
2. Draw a vector operation diagram where the tails of the initial and final momentum vectors are connected.
a. The change in momentum vector points from the head of the initial momentum to the head of the final momentum.
b. The change in momentum is called the impulse and must point in the same direction as the net external force on the system.

3. Use these diagrams to apply the Impulse-Momentum Theorem in the mathematical representation.
$\vec{J}=\Delta{}\vec{p} = \Sigma{}\overline{\vec{F}}_{external}\Delta t$
4. If the change in momentum occurs in two dimensions, you will need to break both the net force and the change in momentum up into components and deal with each separately.
Problems involving the graphical representation.
1. Identify that the area under a net forces as a function of time curve is equal to the change in momentum on the system.
a. If a graph is provided, it should be net force vs. time to be useful to the concept of impulse.
b. If making a graph is useful, be sure to plot the net force on the vertical axis and time on the horizontal.
2. Use of the steps for problems with no explicit graphical representation (above) are still useful when plots are necessary.
a. For a 2D problem, there must be separate plots for each of the components of net force as a function of time that correspond with the change in momentum in that direction.
Misconceptions & Mistakes
- A change in momentum does not have to be a change in both direction and magnitude it can be either a change in direction, or a change in magnitude only.
- It's important to remember that Impulse is defined as the change in momentum, you cannot use impulse if the momentum is constant.
- Momentum is a vector and thus the change in momentum, Impulse is also a vector.
A change in momentum does not have to be a change in both direction and magnitude it can be either a change in direction, or a change in magnitude only. - It's important to remember that Impulse is defined as the change in momentum, you cannot use impulse if the momentum is constant.
- Momentum is a vector and thus the change in momentum; Impulse is also a vector.
- Momentum is equal to velocity scaled by mass. Since mass is always a positive scalar, momentum has the same direction of velocity.
- The change in momentum is equal to the change in velocity scaled by the mass. Since mass is always a positive scalar, the change in momentum has the same direction of the change in velocity.
If the external force acting on your system is not constant (i.e. it varies with time), you can not use the maximum value of that force when finding impulse. You must look at the external force vs time graph and estimate the area under the curve to calculate the impulse. - Impulse is related to changes in velocity scaled by a mass. Thus, we have information about velocities. So do not forget about kinematics; the changes in velocity obtained from impulse can be used with kinematics.
Pro Tips
- If you're given a force applied for some amount of time, Impulse is often a valuable analysis tool.
- For an impulse problem not explicitly involving the graphical representation, use the vector operation for change to determine the change in momentum direction.
- Draw the initial and final momentum vectors with their tails fixed to the same point.
- The change in momentum vector points from the head of the initial vector to the head of the final vector.
- This can help you check that you've done your math correctly.

- Draw the initial and final momentum vectors with their tails fixed to the same point.
Multiple Representations
Multiple Representations is the concept that a physical phenomena can be expressed in different ways.
Physical
Below we can see a car of mass (m) with some 1D velocity moving horizontally to the right.

Here we can understand that a moving car has momentum directed in the same direction as the car's velocity. If that isn't clear, visualize the car moving and hitting into a small object like a rubber ball, how would it behave after the collison? What was transferred to the ball in order to make it behave that way?
Mathematical
Impulse = change in momentum
$ \vec{J} = \Delta \vec{P} = \sum \vec{F}_{ext} \Delta t $
Momentum = mass * velocity
Remember that momentum is a vector quantity comprised of a velocity vector multiplied by a scalar mass quantity.
$\vec{p} = m \vec{v}$

---------------------------------------------------------------------------------------------------------------------------------------------------------------
---------------------------------------------------------------------------------------------------------------------------------------------------------------
---------------------------------------------------------------------------------------------------------------------------------------------------------------

Graphical
The Impulse-momentum theorem states that the change in momentum of a system is equal to the net force multipled by time. In cases where the force is changing, this summation becomes an intergral, which graphically can be visualized as the area under a force vs. time curve. By finding the area of the trapezoid below you can determine the system's change in momentum. Note: this discussion has assumed motion along a line, the approach can be extended into mutliple dimensions by applying a vector analysis.
. 
Descriptive
Lets analyze a rocket launch. At time $t1$ our rocket has some initial mass $m_{1}$ and an initial velocity $\vec{v}_{1}$, giving it a momentum of $\vec{p}_{t1} = m_{1} \vec{v}_{1}$. After some later time $t2$, the rocket has used up some fuel and the mass of the rocket has changed to $m_{2}$, while the velocity has not changed, giving the rocket a different momentum of $\vec{p}_{t2} = m_{2} \vec{v}_{1}$.
Experimental
While you are driving your momentum is mostly dependent on the velocity of your vehicle. Any change in mass of the vehicle and the passengers is negligible, and we may treat the mass as constant. Therefore, as you are driving you can measure your momentum by multiplying the mass of the car plus the passengers with the value of your speedometer.