When light shines on a very thin film, interference can occur. Sometimes the interference pattern can be quite striking, as in the case of an oil slick.
Here is a cool video displaying thin film interference in action.
Pre-lecture Study Resources
Watch the pre-lecture videos and read through the OpenStax text before doing the pre-lecture homework or attending class.
BoxSand Introduction
Wave Optics | Thin Film Interference
Light in a vacuum always travels at a speed c = 2.99 x 108 m/s. When any wave is incident on a boundary, like when light travels from the air onto water, some of the wave is reflected and some of it is transmitted. Experiment will show that light appears to slow down while traveling through the water as opposed to the air. This is called the effective speed ($v_{eff}$) of the light in the medium. The Index of Refraction (n) is a measure of the effective speed of light in a medium.
$n=\frac{c}{v_{eff}}$
Notice, that since nothing can travel faster than the speed of light, that the index of refraction is always greater than or equal to 1. This slowing down of light also causes the wavelength to change.

This is because the constant for a wave across a boundary is the frequency. with $v=f \lambda$, if the frequency is constant and the speed decreases, the wavelength must also decrease. You'll also notice the direction the light travels also changes. The index of refraction can be used to determine how much light bends when traveling from one medium to the next. See Snell's Law of Refraction for more about the bending of light.
When light is incident on a boundary where the index of refraction is changing, some of the light is reflected and some of that light is transmitted. This can have interesting effects when light is incident on a very thin film of certain materials. Consider the situation below, which could represent oil on top of water. Air would be the top surface, oil would be the thin film, and water would be the bottom surface.
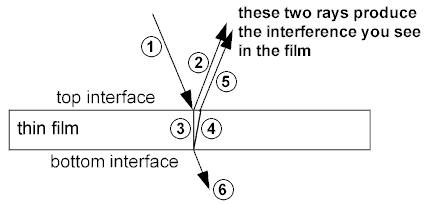
Here light ray (1) is the original light beam incident on the top interface. It splits into two rays - (2) is the reflected ray and (3) is the transmitted ray. The refracted (transimitted) ray (3) then interacts with the bottom interface and the reflected ray is (4) and the transmitted ray is (6). Lastly (4) interacts again with the top surface and some of it is transmitted (5). There are more reflections and transmissions, an infinite number in theory, but the first two are the most dominant due to the intensity decreasing at every interface. Now light rays (2) and (5) can interference with each other. They are coherent since they originated from the same source and there is a Path Length Difference (PLD) between the two. At near normal incidence the PLD is equal to twice the thickness $t$ of the film, $PLD = 2t$. Now before using the standard integer multiple of the wavelength approach to constructive interference, you must first consider phase changes in the reflected rays.
When light reflects off a material with a higher index of refraction the reflected wave has a phase shift. The animation on the left shows a wave pulse on a string that displays the same feature. You can see the pulse coming in from the left is upward but reflects downward, shifting the wave a half of a cycle ($\pi$).
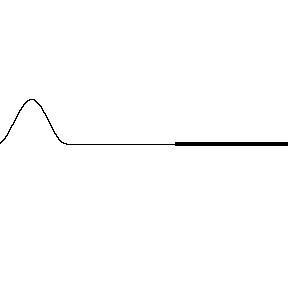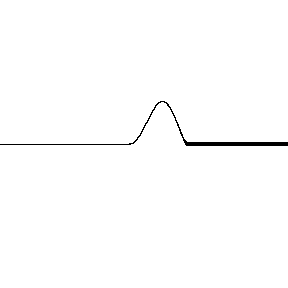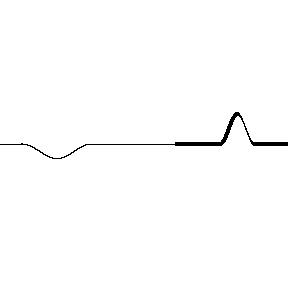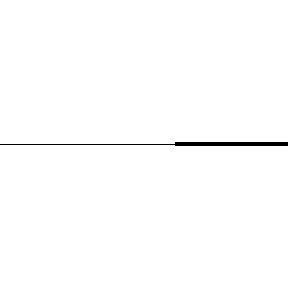 * Images: Dr. Russel
* Images: Dr. Russel 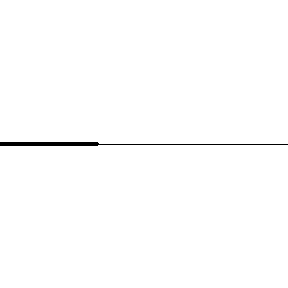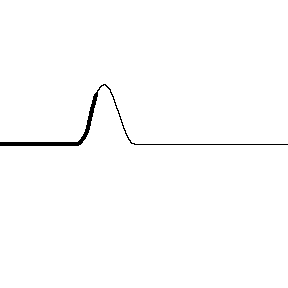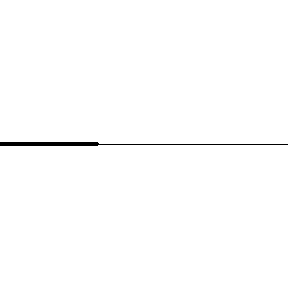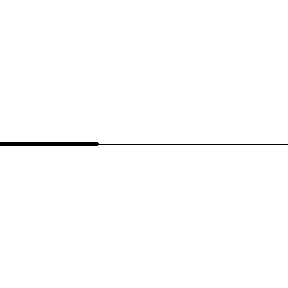
In contrast if light reflects off a material with a lower index of refraction, there is no $\pi$ phase shift. Also notice that the transmitted waves never have any phase shift.
All of this means you have find the relative number of phase shifts between the first reflected wave (2) and the second reflected wave (5). An example would be the air => oil => water system described above. Oil has a higher index of refraction than oil, so ray (2) has a $\pi$ phase shift. When ray (3) reflects off the bottom surface, it is in oil and bouncing off water. Since $n_{water}<n_{oil}$ there is no phase shift in reflected ray (4) or in (5) since it is transmitted. Ray (2) and (5) are interfering but there is a relative phase shift between them. So you must switch the conditionals for constructive and destructive interference.
| m = 0, 1, 2, ... | No relative phase shift ($\phi=0$) | relative phase shift ($\phi=\pi$) |
| Constructive Interference | $2t = m \lambda_{film}$ | $2t = (m+\frac{1}{2}) \lambda_{film}$ |
| Destructive Interference | $2t = (m+\frac{1}{2}) \lambda_{film}$ | $2t = m \lambda_{film}$ |
Here $\lambda_{film}$ is the wavelength of the light in the film. You can use the index of refraction to determine $\lambda_{film}$
The most common place this effect is observed is on bubbles or oil slicks. The colors you see are because those are the wavelegths that match the conditions for more constructive interference. The colors change because there are different thicknesses in the film.


Key Equations and Infographics





Now, take a look at the pre-lecture reading and videos below.
BoxSand Videos
OpenStax Reading
Fundamental examples
(1) Light with a wavelength $\lambda = 88.7 MHz $ is broadcast through a medium with an index of refraction $ n = 3$. What is the wave speed of the broadcast?
(2) An electromagnetic wave traveling through a medium with index of refract $n= 8$ has a wavelength $\lambda = 1.8 nm$. What is its wavelength in vacuum?
(3) You are floating in a pool. Your friend thinks he is such a fast swimmer that he can beat light in a race to the other end of the pool. (your friend is not smart). The pool is 100 m long and you are at one end of it. You have a red laser pointer ($\lambda_{vac} = 700 nm$). (a) If you shine the laser pointer, underwater, long will it take for light to travel down the length of the pool? Your friend swims at a rate of 5 m/s. (b) Who will win the race? Water has an index of refraction $n_w = 1.33$.
Solutions found HERE
Short foundation building questions, often used as clicker questions, can be found in the clicker questions repository for this subject.
(1) Green light with a wavelength $\lambda_{green} = 500 nm$ shines on a soap film (n = 1.33) that has air on either side of it. The light strikes the film perpendicularly. What is the minimum thickness of the film for which an observer would see maximum constructive interference?
(2) Orange light with a wavelength $\lambda_{OJ} = 600 nm $ shines on a soap film ($n_{soap}= 1.33$) that is resting on oil ($n_{oil} = 14 $). The top of the soap film is open to the air. What is the minimum thickness of the film for which an observer standing directly overhead would see maximum constructive interference?
(3) A glass coverslip is floating on oil in a beaker that is open to the air. The index of refraction for the glass is $n_{glass} = 2.5$ and the refractive index of the oil is $n_{oil} = 18$. Janet wants to measure the minimum thickness of the glass so she sets up a laser that will shoot light normally incident to the surface of the coverslip. The laser is capable of scanning through different wavelengths, and through clever experimentation Janet measures that the minimum thickness of the glass is 114 nm. What are two wavelengths at which Janet measured maximum constructive interference?
Solutions found HERE.
Short foundation building questions, often used as clicker questions, can be found in the clicker questions repository for this subject.
Post-Lecture Study Resources
Use the supplemental resources below to support your post-lecture study.
Practice Problems
Conceptual problems
BoxSand's multiple select problems
BoxSand's quantitative problems
Recommended example practice problems
- Openstax has practice problems toward the end of each section, Website Link
For additional practice problems and worked examples, visit the link below. If you've found example problems that you've used please help us out and submit them to the student contributed content section.
Additional Boxsand Study Resources
Additional BoxSand Study Resources
Learning Objectives
Summary
Summary
Atomistic Goals
Students will be able to...
YouTube Videos
Here is a good video on index of refraction,
This is an excellent video on the refractive index,
Doc Schuster dives in and explains thin film interference with an example
This Khan Academy video will help you understand the behavior of light as it passes through and interacts with varying index of the medium.
Simulations
Check out the BU thin film simulation. This is a great way to better understand the physical phenomena.
For additional simulations on this subject, visit the simulations repository.
For additional simulations on this subject, visit the simulations repository.
Demos
For additional demos involving this subject, visit the demo repository
For additional demos involving this subject, visit the demo repository
History
Oh no, we haven't been able to write up a history overview for this topic. If you'd like to contribute, contact the director of BoxSand, KC Walsh (walshke@oregonstate.edu).
Physics Fun
Other Resources
Problem Solving Guide
Use the Tips and Tricks below to support your post-lecture study.
Assumptions
Checklist
1. The index of refraction is quite often used to determine how much light rays bend upon moving from one material to another. The changing directions effect is a direct consequence of the light changing effective speeds. So the first question is if the problem is about light bending at an interface or is about it changing speeds. If its about changing directions, see Snell's Law of Refraction.
2. Determine if the index of refraction is increasing or decreasing so that you know if the speed is increasing or decreasing.
3. If the problem involves wavelengths and frequencies, you may have to use the equation $v=f \lambda$. You may also have to use the fact that the frequency is constant accross a border, the wavelength and speed are not.
4. Solve for the desired quantity.
(1) Sketch out the standard representation for thin-film interference: two horizontal lines, representing 3 separate media. Label on this sketch the indices of refraction of the three media. The middle medium is the "thin film."
(2) Determine the wavelength $\lambda_2$ of your wave inside of the thin film. Remember that maximum constructive interference has to do with whether or not some integer-number of wavelengths fit into some distance, so it is important to know what the wavelength is inside of the medium in which the path-length-difference occurs - which, if you use the standard sketch, is always the middle (or second) medium.
(3a) Determine which equation is appropriate for describing constructive interference. To do this, determine whether or not there is a relative phase-shift between the two waves that are interfering. Remember that, at every boundary, some light is transmitted while some is reflected. The reflected light will have a $\pi$ phase-shift if the index of refraction of the medium the wave is traveling into is greater than that which it is leaving. Using the standard sketch, this means the wave reflected off the top surface will have a phase-shift iff $n_2 > n_1$ and the wave reflected off the second surface will have a phase-shift iff $n_3 >n_2$. Transmitted light does not undergo a phase-shift.
(3b) If there is a $\pi$ relative phase shift, then:
- constructive interference is described by $2t = \left(m + \frac{1}{2}\right) \lambda $, where $t$ is the thickness of the thin film and $\lambda$ is the wavelength of the light within the thin film (so here it takes the value of $\lambda_2$ calculated above, but I have left it as $\lambda$ to be consistent with other resources).
- destructive interference is described by $2t = m \lambda$
If there is no relative phase shift between the two waves, then the equations are swapped and $2t = m \lambda$ corresponds to constructive and $2t = \left( m + \frac{1}{2} \right) \lambda$ corresponds to destructive interference.
You now have all of the variables you need to finish the problem. Depending on the problem, you may be asked for a couple of different things. One might be a "minimum thickness" - in this case, you want to find the minimum possible value you can find for $t$, which corresponds to the smallest possible $m$ value (usually either $0$ or $1$). Or, you may be asked what wavelengths would produce destructive or constructive interference given some thickness - which is as simple as solving $2t = m \lambda$ for $t$ (or the other equation, depending on the situation). Once you have gone through step 3 above, you have all of the info that can be gleaned algorithmically: the rest is down to correctly interpreting the individual problem and what it is asking for.
Misconceptions & Mistakes
- ... treat the wavelength as the constant across a boundary. Frequency is what is constant across a boundary.
- ... try and use Snell's Law for problems that only involve speed or wavelength changes. If the problem does not involve the bending of light, you do not need to use Snell's Law.
- ... believe that a light photon actually travels slower than c. In reality if a photon (bundle of light) exists, it travels at c. In a medium there is vacuum between the atoms and that is where the photons exist. The interaction with the atoms in the medium, via mechanisms like scattering, is what makes the light take longer to travel the same overall distance.
- ... read too much into the statement above. You can just treat the light like it's moving slower than c.
- There is not one simple equation for thin-film interference - the conditions for maximum and minimum interference change based on the parameters of the problem. You must first determine if there are relative phase shifts!
Pro Tips
- Sketch a simple physical representation where the wavelength of the light changes and the speeds are labeled on each side of the boundary.
- Memorize $v=f \lambda$ and $n=\frac{c}{v_{eff}}$
- Frequency is a property of the source, not the medium. Frequency does not change across a boundary.
- Index of Refraction related to speed changes is taught briefly before Thin Film Interference so that you can find the wavelength in the film. If it wasn't for TFI, it would be taught in junction with Snell's Law of Refraction where it is often used as well.
- It's not too hard to use the concept of the speed changing across a boundary, coupled with the frequency not changing, to find the change in the wavelength. That feature, along with speed is distance over time and some geometry, makes deriving Snell's Law as a consequence of the speed changing very doable. Go through that derivation and you will have effectively mastered the concept of the index of refraction (at an introductory physics level).
- Always draw the same picture for thin-film interference problem: two horizontal lines, labeling the indices of refraction of the different media. This will help you get your bearings on the problem and get most of the relevant information on the page
- Being good at thin-film interference problems is all about identifying phase-shifts, since understanding the relative phase-shift between two waves is what dictates which equations to use. Always find phase-shifts first, if you are able, before continuing on the problem.
Multiple Representations
Multiple Representations is the concept that a physical phenomena can be expressed in different ways.
Physical
Mathematical





Graphical
Descriptive
Experimental