In the graphical analysis module, we wish to develop the concepts and tools necessary to interpret and analyze graphs containing information about position, velocity, acceleration, as a function of time. The graphs we will analyze all contain information about the motion of an object. Through the use of these graph, a foundation for a deeper understanding of the underlying physics can be obtained.
This short video lets you connect position, velocity, and acceleration graphs to a cars motion.
Pre-lecture Study Resources
Read the BoxSand Introduction and watch the pre-lecture videos before doing the pre-lecture homework or attending class. If you have time, or would like more preparation, please read the OpenStax textbook and/or try the fundamental examples provided below.
BoxSand Introduction
Graphical Analysis | Graphical Analysis
Understanding motion can be accomplished through the aid of interpreting plots of data. Plots of motion data show how the physical quantities observed change in time. The 3 quantities usually plotted are position, velocity, and acceleration. When plotted these quantities are shown as functions of time, meaning that on the y-axes will be the physical quantity measured, on the x-axes will be time, and the line on the graph shows how that quantity changes in time.
Often in the real life situations the device used to measure features of motion only records one type of physical quantity – an example being if you recorded the velocity of your car as a function of time with the aid of its speedometer. You would like to understand how to use that data to determine other physical quantities, such as your position or acceleration as a function of time.
To go between plots of position, velocity, and acceleration requires two main abilities, determining slopes of plot lines (sometimes curved) and area under the plot lines. There are simple connections between the various plots which can be summarized by the following picture. Clicking on each of the arrows will show you how you can convert from one physical quantity to the next and back again.
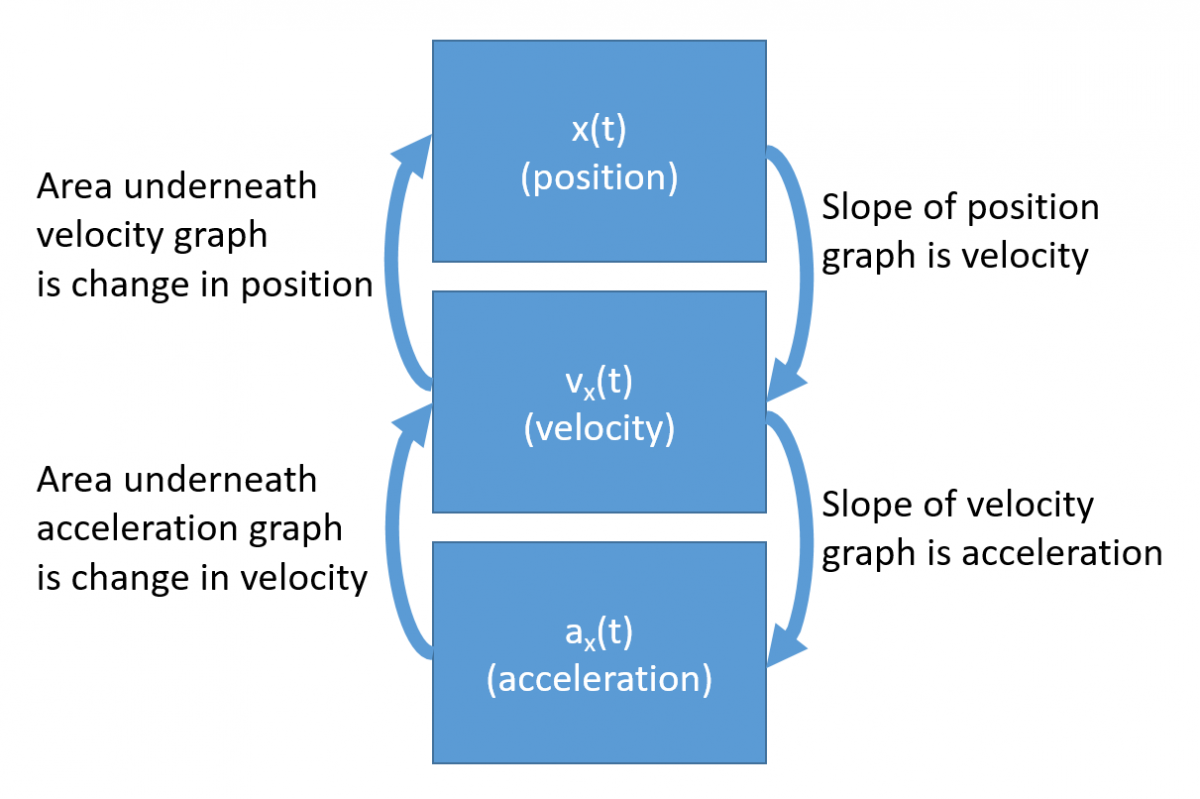
Key Equations and Infographics

Area of a rectangle
ARectangle = Length x Width
Area of a Triangle
ATriangle = 1/2 x Base x Height
Now, check out the pre-lecture reading and videos below for more information on Graphical Analysis
BoxSand Videos
Required Videos
Suggested Supplemental Videos
none
OpenStax Reading
This link takes you to the graphical analysis of kinematics section of the openstax college physics textbook.
Fundamental examples
These are fundamental questions of similar complexity to some lecture template questions. Give them a try now. They may help you organize your mental model for this content in this module.
1.Which of the following position vs time graphs best represent the motion observed in the animation below?


2.Which of the following position vs time graphs best represent the motion observed in the animation below?


For questions 3 - 6, refer to the figure below.
3. Which graphs have constant displacement?
4. Which graphs have constant velocity?
5. Which graphs have constant non-zero acceleration?
6. For graph c below, sketch a position vs time and acceleration vs time graph.

CLICK HERE for solutions.
Short foundation building questions, often used as clicker questions, can be found in the clicker questions repository for this subject.
Post-Lecture Study Resources
Use the supplemental resources below to support your post-lecture study.
Practice Problems
Recommended example practice problems
Set 1: Problems 22-24
Set 2: Lots of great problems to choose from
Set 3: 10 quick questions
Problem sets with solutions
- https://www.physicsclassroom.com/morehelp/graphs
- https://physics.info/motion-graphs/practice.shtml
- https://student.pattersonandscience.com/Lesson%20content/10%20Science%20C...
- https://www.redknightphysics.com/kinematicsProbs.php
Problem sets without solutions
- https://physics.info/motion-graphs/worksheet-choose-velocity.pdf
- https://physics.info/motion-graphs/worksheet-choose-displacement.pdf
Video Solution to Example Problems
- Displacement from time and velocity example- https://www.khanacademy.org/science/physics/one-dimensional-motion/displ...
Worked Examples
- Motion Graphs Acceleration, Velocity, and Position.(youtube)
- Also gives a great recap on the sections
- Motion Graphs Example Problem(youtube)
- This entire video series, 22 videos, good titles for searching what you want to find
Additional Boxsand Study Resources
Additional BoxSand Study Resources
Learning Objectives
Summary
The objective is for students to be able to go between the graphical representation and all other representations (descriptive, physical, mathematical, experimental). This includes the ability to move between position, velocity, and acceleration quantities.
Atomistic Goals
Students will be able to...
- Interpret a position versus time graph to determine the position of the object at any given time, is it positive, negative, or zero.
- Interpret a position versus time graph to determine if it is traveling in the positive or negative direction.
- Interpret a position versus time graph to determine if the object is speeding up or slowing down.
- Interpret a velocity versus time graph to determine what the velocity of the object is at any given time.
- Interpret a velocity versus time graph to determine if an object is traveling in the positive or negative direction.
- Interpret a velocity versus time graph to determine if the object is speeding up or slowing down.
- Interpret an acceleration versus time graph to determine what the acceleration of the object is at any given time.
- Interpret an acceleration versus time graph to determine if the object is speeding up or slowing down.
- Show on a graph an example of instantaneous velocity and instantaneous acceleration.
- Show on a graph an example of average velocity and average acceleration.
- Differentiate between the magnitude and direction when interpreting plots.
- Demonstrate the ability to estimate an area under a non-linear curve by breaking the complex curve into more simple well known shapes.
- Recognize what the area under the curve determines, i.e. it represents in changes in position and velocity and not the actual position or velocity, you need to add the change to the initial conditions to find the final state.
- Differentiate between the features of positive and negative area.
- Take a graph of position, velocity, or acceleration vs time and be able to sketch all other graphs from the original. Here is where slopes, areas, and initial conditions are involved.
- Determine if a set of position, velocity, and accelerations could be describing the motion of the same object.If given a graph of position, be able to describe the acceleration of the object by analyzing the slope of the slope of position vs. time and/or determining the curvature and concavity.
- Create graphs of position, velocity, and acceleration for the motion of an object given a written description or experimental demonstration.
- If given a shape of a graph translate the nature of the function into the math representation, e.g. a straight line on a graph is a linear function of the form $y = mx + b$.
- Recognize when to use the graphical representation to analyze systems that would be more difficult in the other representations.
- Use data tables to create graphs and analyze the position, velocity or acceleration of the an object.
- Demonstrate making approximations to slopes or areas when analyzing position, velocity, and acceleration vs. time graphs.
YouTube Videos
This Khan Academy video does a great job of showing the difference between instantaneous speed, velocity, for one dimensional motion. There's a bit towards the end that involves a bit of history and a note about calculus, the video does not use that calculus though, when it does an example.
Doc Schuster has created a wonderful series on youtube to help students understand their physics. This video is a fairly in-depth example involving average velocity. This video also shows how you are not anchored to using the average velocity equation as it is given, you are free to preform any algebraic manipulation you would with any other equation.
Simulations
This simulation helps visualize how slops and areas look like with different graphs. Note that this is just our favorite simulation that relates to graphical analysis. There are other simulations we found that are also related to graphical analysis; those can be found in the simulations repository located here.
-
Try the last two options under drawing tools first before moving on to more silly looking shapes.
-
The graph f(x) vs x is just a general quantity f(x) plotted against the independent variable x. For our purposes now, f(x) would be our velocity, and x would be our time. So we can replaced f(x) vs x with our more familiar v(t) vs t. (velocity vs time). Also note, we often use shorthand notation and just write velocity vs time as ( v vs t ).
-
Under the “View” menu, think of integral as area and derivative as slope.
-
When viewing the graphs, df/dx can be interpreted as the slop of f(x). The value of this df/dx vs x graph at a specific x would be the value of the slope of f(x) at the same x. In our context, the value of df/dx at a specific x is the value of the slope of v(t) at a specific t (time). This value of the slop of v(t) at a specific time is the instantaneous acceleration.
-
The fun looking $ \int_{0}^{x} f(x') dx'$ expression can be interpreted as the area. The value of this graph at a specific x would be the value of the area from x=0 to x. In our context, the value of this graph at a specific time t, would be the value of the area from t=0 to t. This value would then be our displacement.
The moving man simulation helps with understanding position,velocity,and acceleration graphs.
For additional simulations on this subject, visit the simulations repository.
Demos
Some examples from Flipping Physics.
This video shows two balls dropped, one right after the other. We use the graphical representation in class to determine what happens to the distance between the two as they fall.
For additional demos involving this subject, visit the demo repository
History
Oh no, we haven't been able to write up a history overview for this topic. If you'd like to contribute, contact the director of BoxSand, KC Walsh (walshke@oregonstate.edu).
Physics Fun
Other Resources
This link provides a short overview of how position vs time graphs relate to an objects motion, specifically its velocity.
This link provides a short overview of how velocity vs time graphs relate to an objects motion, specifically its acceleration.
Resource Repository
This link will take you to the repository of other content on this topic.
Problem Solving Guide
Use the Tips and Tricks below to support your post-lecture study.
Assumptions
- Many physical phenomena can be represented and understood more holistically in graphical form.
- Quantities can be related to each other through graphs, both through the relationship between the x and y axes, but also through more nuanced qualities such as the slope and area under the curve of a graph.
- The slope of a position vs. time curve gives the velocity, the slope of velocity vs. time curve gives acceleration.
- The area underneath an acceleration vs. time curve gives the velocity at a particular time, while the area under a vleocity vs. time curve gives the position at a particular time.
Checklist
Identify the quantities being graphed
Identify the units being used
Identify the scale of the axis
2. Determine what information you need to extract
3. Consult this chart

4. Carry out the procedure outlined in the chart to find the relevant quantity that you are looking for
Misconceptions & Mistakes
- Do not forget to look at the axis to identify the quantities being plotted and their respective units.
- Do not forget that when we find the slope or area of a graph, the result has units.
- If the acceleration of an object is zero, that does not necessarily mean the velocity of that object is also zero.
- Calculating the slope (Δx/Δt), gives the average velocity, not the instantaneous velocity. There is a special case where if your position vs time graph is linear, then the slope will also be the instantaneous velocity. A similar statement can be made when calculating the slope of velocity vs time producing the average acceleration.
- A properly labeled graph contains all the same information as the kinematic equations.
- Keep in mind the sign of the slope (or area) when drawing the line of the next graph, positive slope (or area) it should be a positive line and vice versa.
Pro Tips
- When visualizing the slop at a specific time of a position vs time graph, the tangent line at a specific time is the instantaneous velocity at that time. A similar statement for visualizing the slope at a specific time of a velocity vs time graph can be made for instantaneous acceleration.
- If given a graph of position vs time, drawing a graph of velocity vs time and acceleration vs time is easiest if you align the graphs vertically, with the origin of each graph left aligned. This way all the interesting features at specific times of each graph line up vertically. This is in contrast to how many students and textbooks align the graphs horizontally, which makes it harder to sketch graphs. For example: the timestamps for each graph a lined up when we switch to the new layout and the interesting feature at 2s is easily seen in each of the graphs.

- If the shape of a graph is curved, or anything but linear, you can estimate the area under the curve by dividing the shape into squares, rectangles, and triangles. By increasing the resolution (i.e. using more squares, rectangles, and triangles), you can improve the accuracy of your estimate.
- To check if your graph makes sense look at a small sliver of time at different parts of the graph and compare it between them. For example, if the velocity is constantly increasing a small sliver of time at the beginning of the position graph should change less in the position direction than a small sliver of time at the end of the position graph.
Multiple Representations
Multiple Representations is the concept that a physical phenomena can be expressed in different ways.
Physical
Everytime you see a graph having to do with a physical situation, it is important to try and represent what looks like in the real world with a simple drawing. Later problems will often call for translating pictures and text into graphs and getting practice going back and forth between them will quickly develop a high level of comfort with graphical analysis and its application in the world of physics.
Mathematical

Area of a rectangle
ARectangle = Length x Width
Area of a Triangle
ATriangle = 1/2 x Base x Height
Graphical
The Physics Classroom introduces the relationship between kinematics equations and their graphical representation. In addition, for a more in-depth discussion please refer to the graphical analysis section.
Descriptive
Decriptions of graphs can often be literal statements about the graph itself. However, tying in the physics, we can discuss what was once a purely mathematical description as a description of the real world. Get use to thinking about the slope of a position vs. time graph as the velocity, it will always be true! Get to the point of seeing and thinking about that relationship when you look at position graphs and being able to fluidly understand and communicate what is happening in graphical problems will open up to you!
Experimental
Explore graphical relationships in everyday situations. Try to determine the position, velocity, and acceleration graphs of a section of a bus ride, when going down a hill on a bike, or just walking across campus to class, etc. Go further, and film or time it and get real results for your position, then you can graph your position vs. time and use it to determine your velocity and acceleration!