Required Videos

Suggested Supplemental Videos

Summary

Summary

Atomistic Goals

Students will be able to...

Electic Field  |  Field Patterns

Charge Distribution Field Patterns

The electric field from a distribution of charge, like that on a charged rod, is fundamentally a superposition of all the fields from the individual charges. Electric fields add by the principle of superposition, which is to say they add linearly and like all other vectors we've learned about.

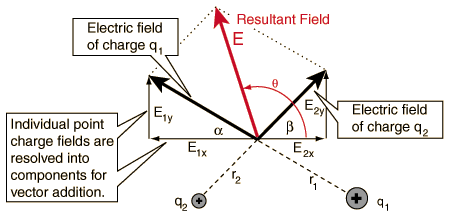                   $\overrightarrow{E}_{net} = \sum \overrightarrow{E}_i$

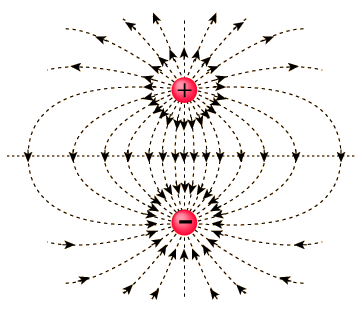
Sometimes the physics representation of a field is presented in the form of Field Lines, where the strength of the field is larger where the lines are more closely spaced. In the field line representation, field lines start at positive charges and end on negative charges. The diagram below is the eletric field for a dipole.

Through superposition, the net field for a number of charge distributions can be determined. It's interesting to note that the electric field for a zero dimensional charge (a point charge) falls off like 1/r² - the field for a one dimensional line of charge falls off like 1/r - and the field from a two dimensional sheet of charge doesn't fall off at all. It's no coincidence that as you increase the dimensions of the charge distribution, the field decreases how fast it falls off.

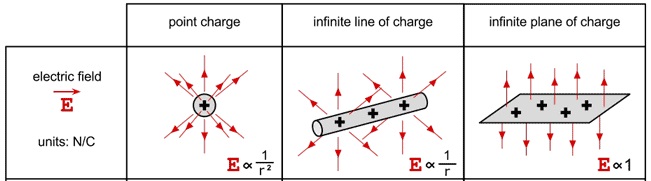
The Electric Field due to an Infinite Sheet of Total Charge $Q$

$|\overrightarrow{E}_{net}| = \frac{Q}{2 \epsilon_0 A}$,      where $\epsilon_{0} = 8.85 x 10^{-12} F \cdot m^{-1}$, and $A$ is the area of the sheet.

If the sheet is infinite or you are close to a finite sheet, the field doesn't even decrease with increased distance. As you move further away from the plate, the electric fields from charges further and further away start to add more constructively, causing the field to remain constant. Putting two plates separated by some distance, with opposite charges, is called a Parallel Plate Capacitor. The fields inside the plates are uniform and provide an excellent tool for studying electric fields. 

Key Equations and Infographics

Now, take a look at the pre-lecture reading and videos below.

OpenStax Section 18.7  |  Conductors and Electric Fields in Static Equilibrium

OpenStax Section 18.8  |  Applications of Electrostatics

For additional simulations on this subject, visit the simulations repository.

Check out the field patterns displayed in this video.

https://www.youtube.com/watch?v=63FnT0W-Hxc

For additional demos involving this subject, visit the demo repository

Oh no, we haven't been able to write up a history overview for this topic. If you'd like to contribute, contact the director of BoxSand, KC Walsh (walshke@oregonstate.edu).

Resource Repository

This link will take you to the repository of other content related resources.

Multiple Representations is the concept that a physical phenomena can be expressed in different ways.

Physical

Mathematical

Graphical

Descriptive

Experimental

(1) What is the magnitude of the Electric field at a location $r = 2 \hspace{0.2 cm} nm$ from a point charge with charge $q=10 \hspace{0.2 cm}nC$ that is located at the origin?

(2) Three point charges $q_1 = q_2 = q_3 = 5 \hspace{0.2 cm}nC$ are placed equidistant from each other on the x-axis: $q_1$ is located at $x= -2 \hspace{0.2 cm}nm$, $q_2$ is located at the origin, and $q_3$ is located at $x = 2 \hspace{0.2 cm} nm$. A point charge $q_4 = 1\hspace{0.2 cm} nC$ is placed on the y-axis, 2 namometers up from the origin. (a) What is the magnitude of the electric force that $q_4$ feels? (b) What is the direction of the electric force on $q_4$? (c) What is the direction of the electric force if $q_4 = -1 \hspace{0.2 cm}nC$ instead?

(3) A point charge $q_1 = -20 \hspace{0.2 cm}nC$ is located at a position $r_1 = <-3,0> \hspace{0.2 cm}nm$. (a) What is the magnitude of the electric field at point $r_a = <0, 3> \hspace{0.2 cm}nm$. (b) By what factor does the magnitude of the electric field at point $r_a$ decrease if another point charge with magnitude $q_2 = 20 \hspace{0.2 cm}nC$ is placed at the origin? (c) Calculate the magnitude and direction of the force that a point charge with magnitude $q_3 = -1 \hspace{0.2 cm}nC$ would feel if it were placed at position $r_a$ for both cases (a) and (b). [Optional (d) What is the electric force on $q_3$ if charge $q_1$ is removed?]

(4) (More time-consuming - practice with computing the electric field from multiple source charges in an arbitrary configuration) Three point charges $q_1 = 5 \hspace{0.2 cm}nC$, $q_2 = 10 \hspace{0.2 cm}nC$, and $q_3 = -2 \hspace{0.2 cm}nC$ are placed as follows: $q_1$ is located at $r_1 = <- 3,0> \hspace{0.2 cm}nm$, $q_2$ is located at $r_2 = <0,0> \hspace{0.2 cm}nm$, and $q_3$ is located at $r_3 = <1, 2> \hspace{0.2 cm}nm$. (a) What is the magnitude and direction of the electric field at point $r_p = <8, 8> \hspace{0.2 cm}nm? 

Solutions found HERE

Short foundation building questions, often used as clicker questions, can be found in the clicker questions repository for this subject.

BoxSand practice problems - Answers

BoxSand's multiple select problems

BoxSand's quantitative problems

Recommended example practice problems 

• *OpenStax, has practice problems at the end of every section
  • Electric Field: Concept of a Field Revisited, Website Link
  • Electric Field Lines, Website Link
  • Conductors and Electric Fields, Website Link
• PhysicsClassroom, 27 problems on charge and the electric field, Website Link
• University of Greenbay: Guided problem on the electric force, Website Link

For additional practice problems and worked examples, visit the link below. If you've found example problems that you've used please help us out and submit them to the student contributed content section.