When finding the work done by various types of forces, an interesting result arises from the work done by gravity and elastic springs. The work done by both types of forces only depends on the initial and final positions of the object. This means that we can skip the process of calculating work for gravity and springs, and instead write a function that results in the same value that we would have got if we did calculate the work the traditional way. The functions we define in place of the work due to gravity and springs, are called potential energy functions. This section will help familiarize you with working with potential energy functions. For completeness the potential energy functions that arise from the work due to gravity and the work due to a spring are the following:
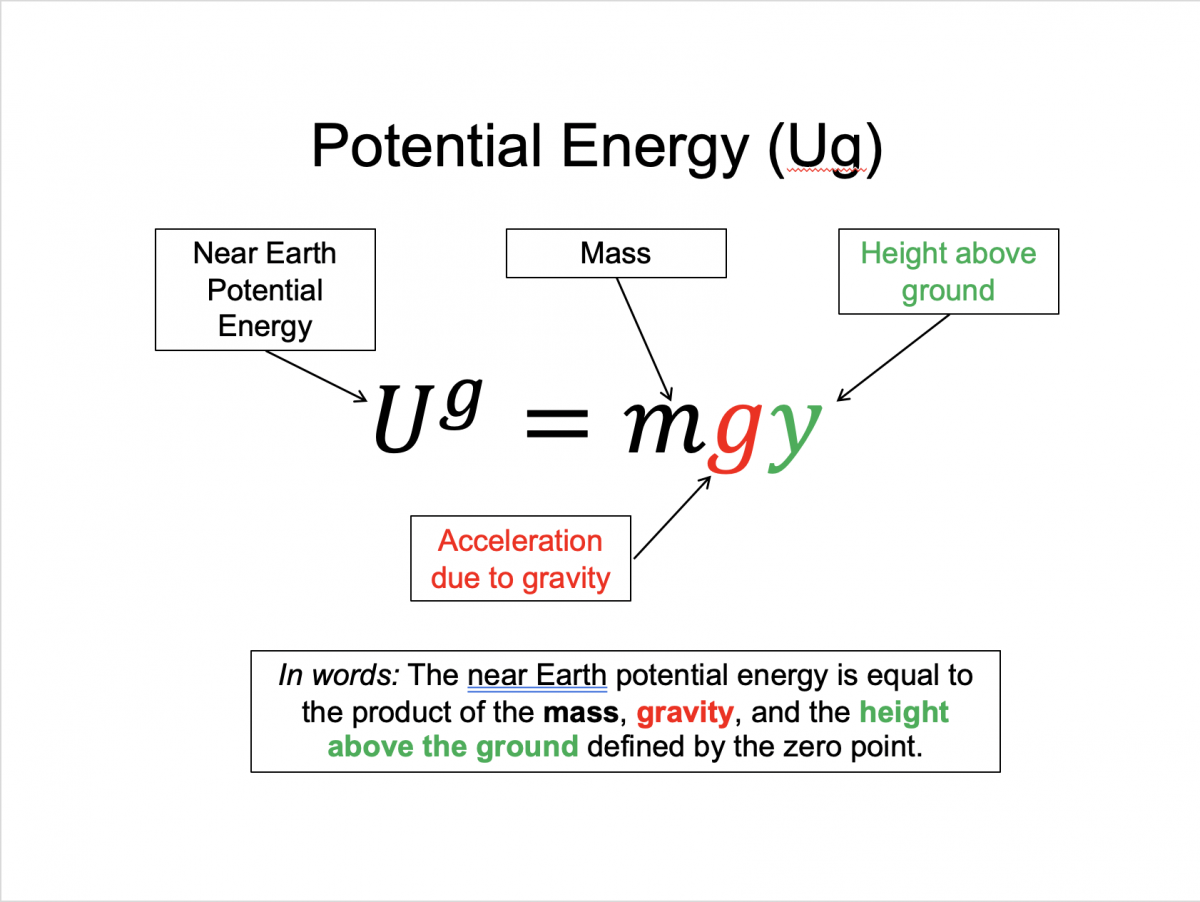
Gravitational potential energy ($U^g$): $mgy$, where m = mass, g = gravitational constant, y = height relative to zero
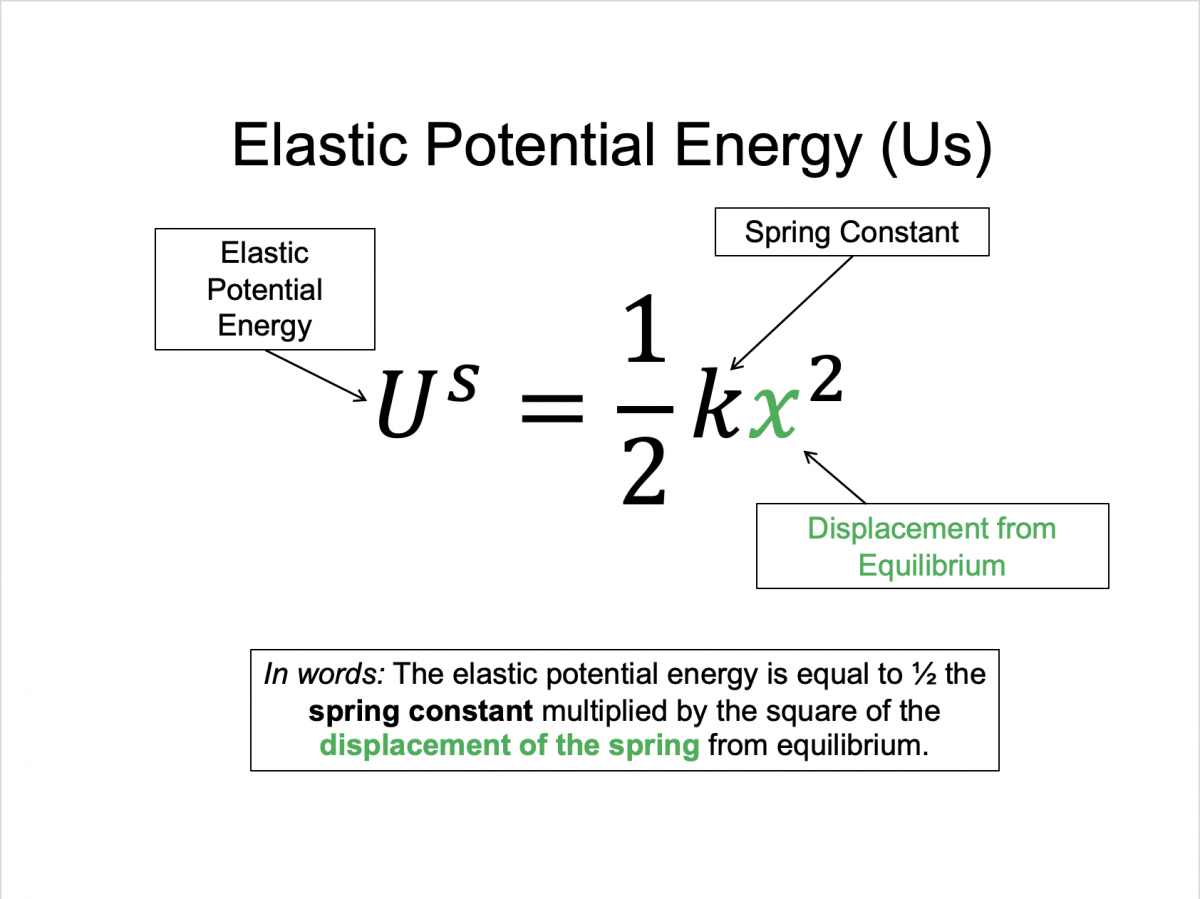
Spring potential energy ($U^S$): $\frac{1}{2}k \Delta x^2$, where k = spring constant, x = distance from equilibrium
If we account for all the interactions an object experiences, we can write a clever summation of specific quantities that will help us describe the motion of the object. The clever expression is known as the conservation of (mechanical) energy. Mathematically it is written as:
$K_i + U^g_i + U^S_i + \sum W_{nc} = K_f + U^g_f + U^S_f$
where K = kinetic energy and U = potential energy. In later sections we will expand on this equation to include more potential energy functions, but for now gravity and spring are the only ones we have came across thus far. Recall energy is a scalar, thus application of conservation of energy will greatly simplify otherwise complicated problems if trying to use kinematics.
Check out the OpenStax trailer to learn about the interplay between kinetic and potential energy.
Pre-lecture Study Resources
Read the BoxSand Introduction and watch the pre-lecture videos before doing the pre-lecture homework or attending class. If you have time, or would like more preparation, please read the OpenStax textbook and/or try the fundamental examples provided below.
BoxSand Introduction
Converation of Energy | Potential Energy and Conservation of Energy
When calculating the work from certain forces, it is discovered that although the work depends on the change in position $\Delta \overrightarrow{r}$ it does not depend on the path that the object took from the initial to final position. We call these conservative forces and for our study we are going to limit ourselves to gravity and elastic springs. This allows us to break the work up into conservative and non-conservative work.
$W = W_{c} + W_{nc}$
Since the conservative work only depends on the change in location - it is path independent - we can define a function of position to account for the work from the conservative forces. An example is the work from gravity (near Earth) is always $W^g = mg \Delta y$, where y is the displacement in the vertical direction from the initial to final location (for more on how this is true see BoxSand's pre-lecture videos below). Since this only depend on the vertical displacement we can account for this work by defining what is called a potential energy function, $U_g=mgy$, and thus the change in potential energy is equal to negative the work.
$\Delta U^g=-W^g=mg \Delta y$
Now we never have to calculate the work from gravity again, we can simply set a new type of initial and final energy, namely the potential energy.
$U^g=mgy$
Now lets make an addendum to the conservation of energy equation.
Recall, $K_i +\Sigma W = K_f$
with, $W = W_{c} + W_{nc}$, and $W_c=- \Delta U^g$
we get, $K_i + (-\Delta U^g) + \Sigma W_{nc} = K_f$
which can be rearranged to yield, $K_i + U_i + \Sigma W_{nc} = K_f + U_f$
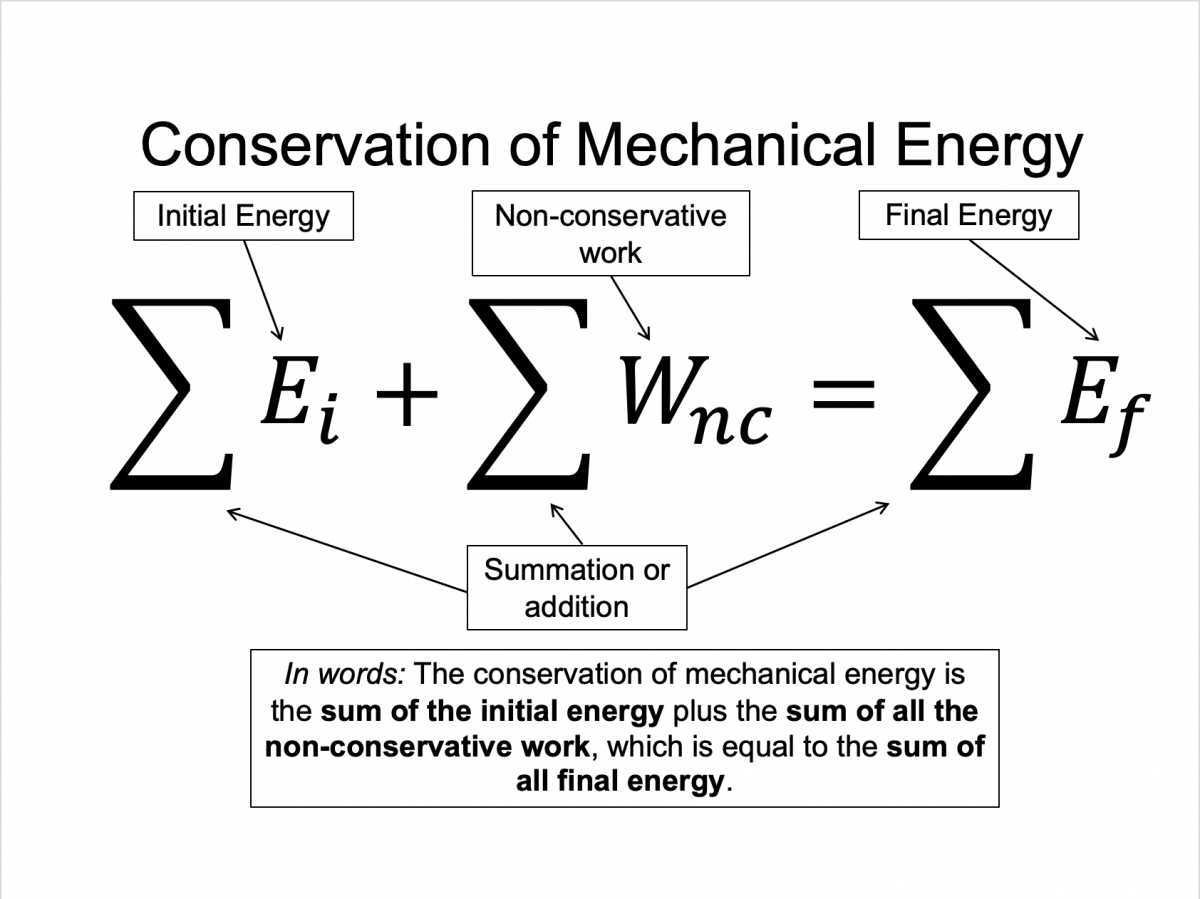
Mechanical energy (E) is defined as kinetic plus potential energy (E = K + U), using this notational simplification we arrive at the final form of conservation of (mechanical) energy. This is how you start all energy problems!
$E_i + \Sigma W_{nc} = E_f$
Which says take the initial energy of the system, kinetic plus potential, and add to that the work from non-conservative forces (everything but gravity and elastic springs), and set that equal to the final energy of the system.
If the above explanation is confusing, use the end result and start getting a feel for the mechanics by applying the theorem and using the equations below.
$K = \frac{1}{2}mv^2$
Gravity: $U^g = mgy$
Elastic Spring: $U^s = \frac{1}{2}kx^2$
$E = K + U$
$E_i + \Sigma W_{nc} = E_f$
Key Equations and Infographics

Now, take a look at the pre-lecture reading and videos below.
BoxSand Videos
Required Videos
Potential Energy and Conservative Forces (12 min)
Potential Energy of Gravity (3 min)
Suggested Supplemental Videos
none
OpenStax Reading
OpenStax Section 7.3 | Gravitational Potential Energy
OpenStax Section 7.4 | Conservative Forces and Potential Energy
OpenStax Section 7.5 | Nonconservative Forces
Fundamental examples
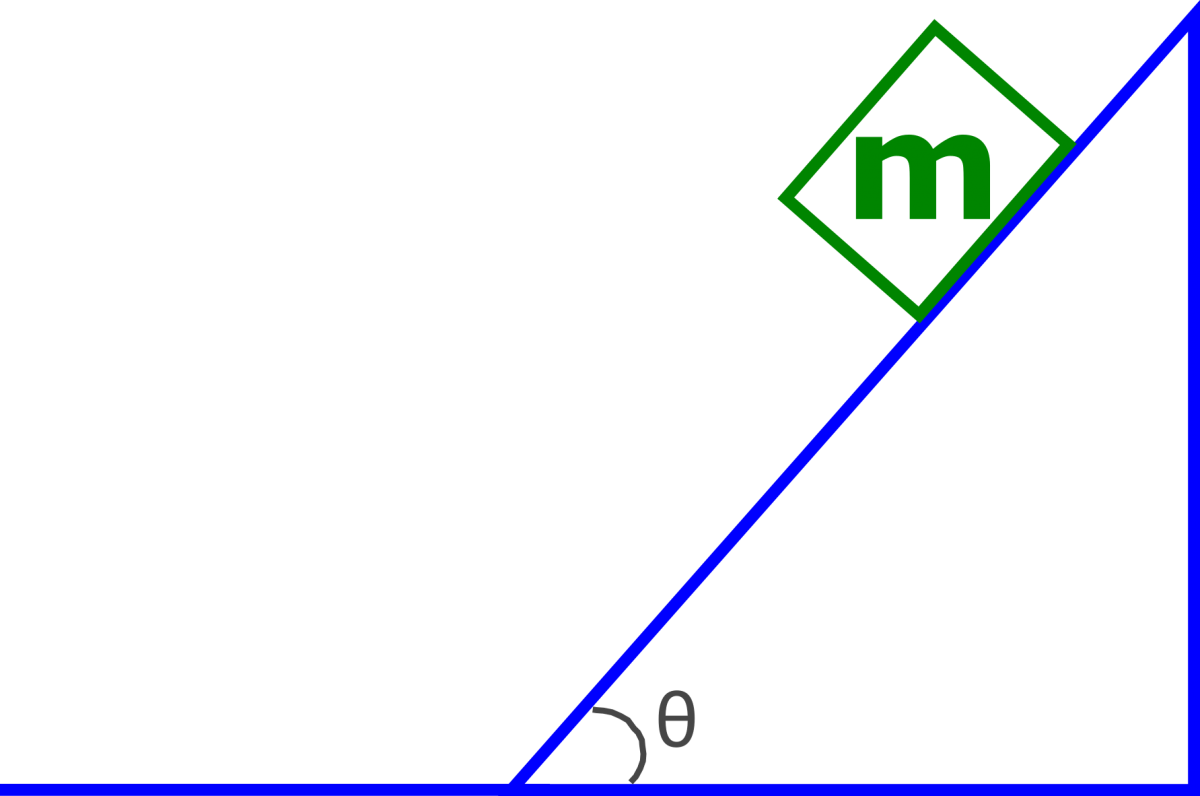
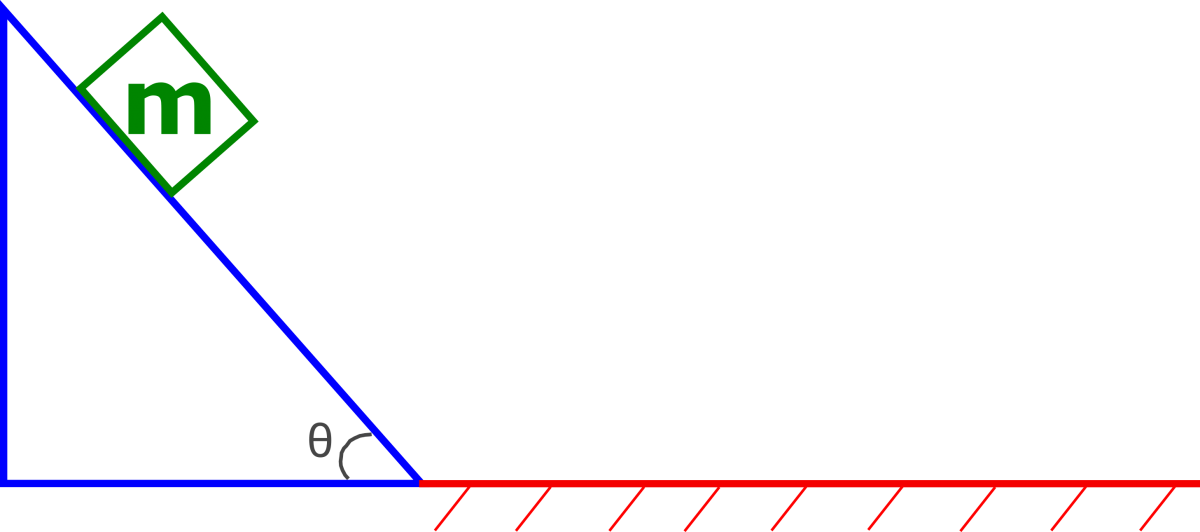
1. A $5 \, kg$ object starts from rest and slides down a frictionless incline as shown in the image below. If the angle shown in the image is $30^{\circ}$, and the object was initially $7 \, m$ up the incline (measured along the incline), what is the velocity of the object at the bottom of the incline?
2. A $7 \, kg$ object starts from rest and slides down a frictionless incline as shown in the image below. All surfaces are frictionless and the spring has a spring constant of $1900 \, N/m$. If the angle shown in the image is $40^{\circ}$, and the object was initially $7 \, m$ up the incline (measured along the incline), what is the maximum compression of the spring?

3. A $7 \, kg$ object starts from rest and slides down a frictionless incline as shown in the image below. The object then encounters the level ground where the coefficient of kinetic friction between the two surfaces is known to be $\mu_k = 0.20$. If the angle shown is $\theta = 20^{\circ}$, how far does the object travel from the base of the incline before coming to rest? The object was initially $7 \, m$ up the incline (measured along the incline).
CLICK HERE for solutions.
Short foundation building questions, often used as clicker questions, can be found in the clicker questions repository for this subject.
Post-Lecture Study Resources
Use the supplemental resources below to support your post-lecture study.
Practice Problems
Recommended example practice problems
BoxSand's Quantitative Practice Problems
BoxSand's Multiple Select Problems
Set 1:Multiple choice problems 25,26 PDF
Set 2: UoW-Greenbay: Stopping distance of a roller coaster, Ball Launched with spring,
Set 3: Physics.info set for Conservation of Energy, Website
For additional practice problems and worked examples, visit the link below. If you've found example problems that you've used please help us out and submit them to the student contributed content section.
Additional Boxsand Study Resources
Additional BoxSand Study Resources
Learning Objectives
Summary
The work energy theorem, combined with knowledge of potential energy functions, allows for the construction of the final form of the conservation energy equation. The goal is to apply the conservation of energy equation to various systems and understand the transformational nature of energy.
Atomistic Goals
Students will be able to...
- Define a system and identify internal and external objects, forces, and work.
- Show that conservative forces yield work that is independent of the path taken.
- Identify conservative and non-conservative forces and work.
- (UPMF) Use the independence of path for conservative work to create a function of position to account for conservative work. We call that
- function a potential energy function for all internal conservative work.
- Construct the final form of the work-energy theorem using the concept of potential energy.
- Show that energy is conserved for systems where the net external work is zero.
- Show that application of an energy analysis involves bookkeeping an initial and final state of the system.
- Use the gravitational potential energy function, for near Earth objects, in an energy analysis.
- Use the spring potential energy function for Hooke's law springs in an energy analysis.
- Construct the graphical representation depicting the kinetic, potential, thermal, and total energy as a function of position.
- (UPMF) When non-conservative work is internal to a system, there is a form of energy associated with that work and it is not called potential energy. E.g. work done by friction converting macroscopic kinetic energy to microscopic kinetic energy (aka thermal energy)
- Identify other forms of energy such as thermal, chemical potential, electric potential, sound, light, … etc.
- Identify energy transformations within a system and energy transfers into/out of a system.
- Apply a conservation of energy equation for a system from its initial to final state.
- Apply conservation of energy to system with multiple internal objects.
- Define elastic collisions and apply a conservation of energy and momentum analysis to the collision.
- Define inelastic collisions and apply a conservation of energy and momentum analysis to the collision.
- Derive the relationship between kinetic energy and momentum.
YouTube Videos
Simulations
Here is a PhET simulation exploring spring potential energy:
Here is a simulation bring together spring potential energy, gravitational potential energy, and some basic conservation ideas:
A fun simulation that lets you build your own rollercoaster and discusses potential energy and some conservation of energy ideas is:
For additional simulations on this subject, visit the simulations repository.
Demos
History
Oh no, we haven't been able to write up a history overview for this topic. If you'd like to contribute, contact the director of BoxSand, KC Walsh (walshke@oregonstate.edu).
Physics Fun
Oh no, we haven't been able to post any fun stuff for this topic yet. If you have any fun physics videos or webpages for this topic, send them to the director of BoxSand, KC Walsh (walshke@oregonstate.edu).
Other Resources
This link takes you to the potential energy page of the physics classroom website. Here they discuss potential energy, including both gravitational potential energy and elastic potential energy.
Resource Repository
This link will take you to the repository of other content on this topic.
This link will take you to the repository of other content related resources.
Problem Solving Guide
Use the Tips and Tricks below to support your post-lecture study.
Assumptions
Checklist
Misconceptions & Mistakes
Pro Tips
Multiple Representations
Multiple Representations is the concept that a physical phenomena can be expressed in different ways.
Physical
Mathematical
Graphical
Descriptive
Experimental