Conduction, convection, and radiation are the three different ways energy can be transfered via heat. Conduction is when energy transfers from one molecule to the next via collisions. Imagine higher energy (greater temp) particles on the inside of a window bumping into their neighbors, when then bump in their neighbors and so on. Eventually some of the thermal energy from the warm side of the window, escapes on the cold side through these collisions. Convection is when a high energy particle literally moves from the a warmer area to a colder area, thus decreasing the thermal energy in the warmer area and increasing it the colder. Radiation is heat transfer electromagnetic waves and all objects with temperature greater than zero (Kelvin) radiate electromagntic waves - think night vision goggles that "see" thermal images.
This concept trailer from OpenStax motivates conduction, convection, and radiation through cooking.
Pre-lecture Study Resources
Watch the pre-lecture videos and read through the OpenStax text before doing the pre-lecture homework or attending class.
BoxSand Introduction
Thermo | Heat Transfer Mechanisms: Conduction, Convection, and Radiation
So far we have discussed heat as it relates to the first law of thermodynamics where we learned that heat is a way for systems to exchange energy, similar to work. We then discussed specific heat and heat of transformation under the section "Heat", but really we were just talking about energy transfers where heat was the most common way to transfer that energy, as opposed to work. What have not yet discussed is the specific mechanisms by which energy is transferred via heat. There are three main mechanisims for heat transfer, conduction, convection, and radiation.
Conduction: Thermal energy, which quantifies the motion of microscopic particles, can be transferred by faster moving particles colliding with slower moving particles and transferring some of their momentum - and thus kinetic energy. Conduction is the primary heat transfer mechanism for solids, where atoms in the crystalline lattice that are wiggling a great deal due to their high thermal energy, start to make the atoms next to them wiggle more. This wiggle-transfer, from one atom to the next, is the primary conceptual understanding of conduction.
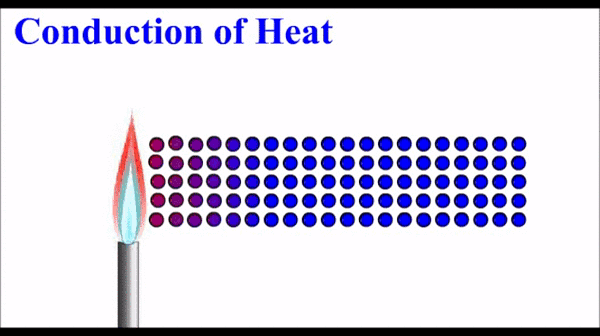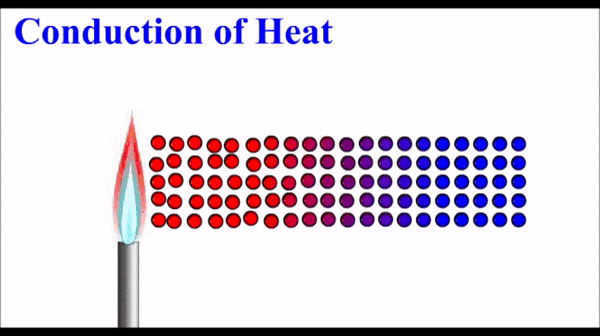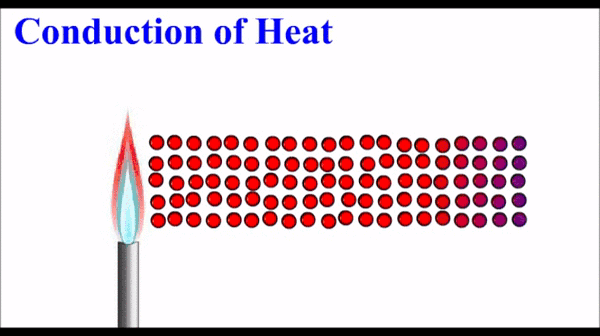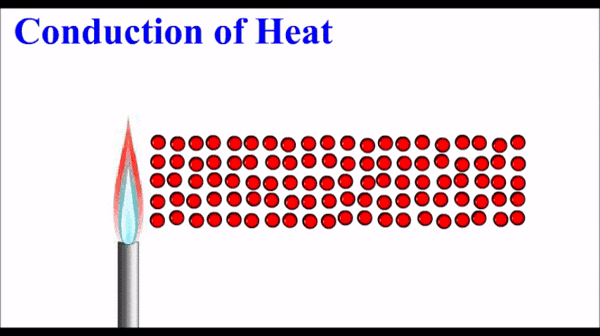
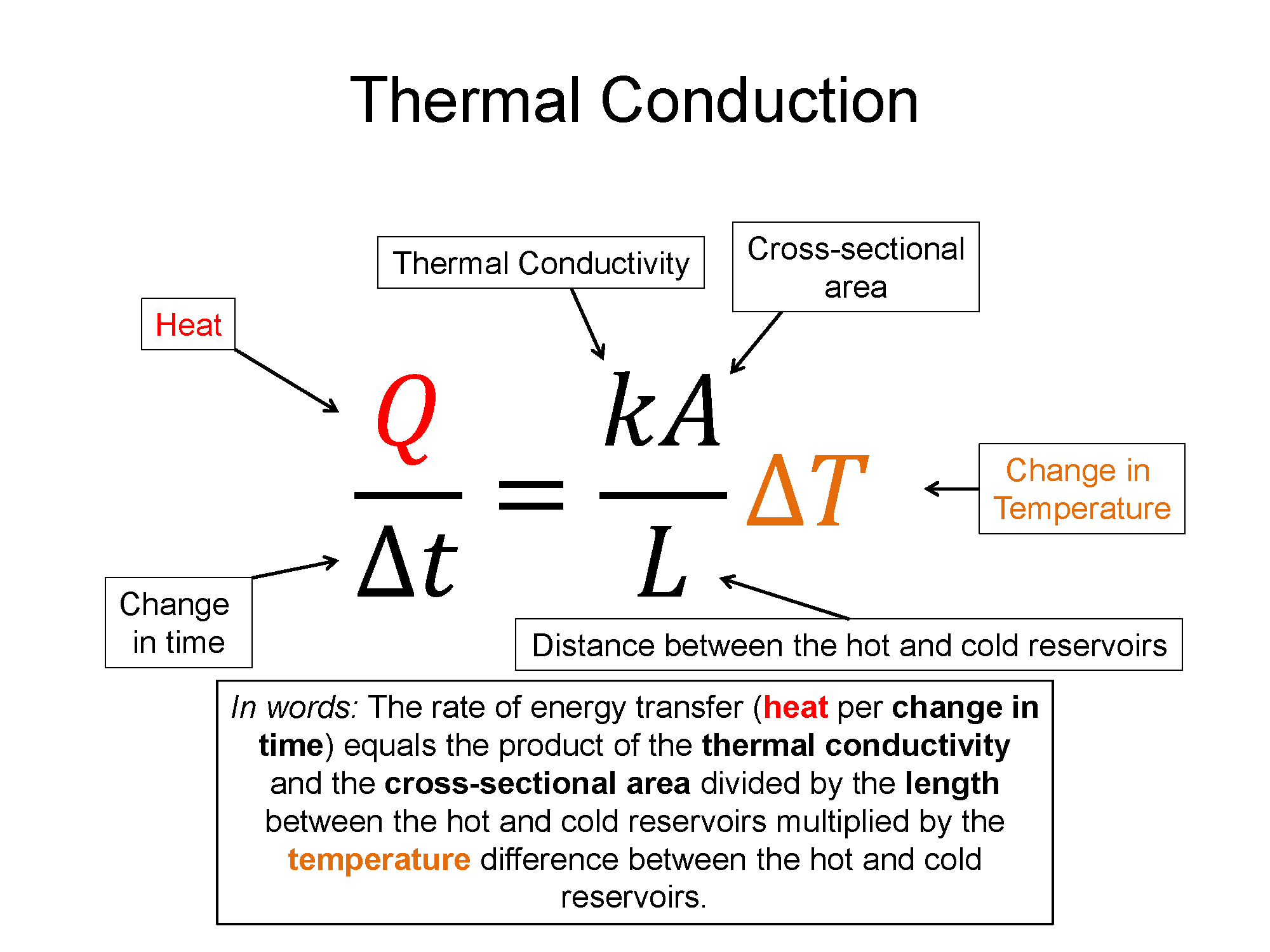
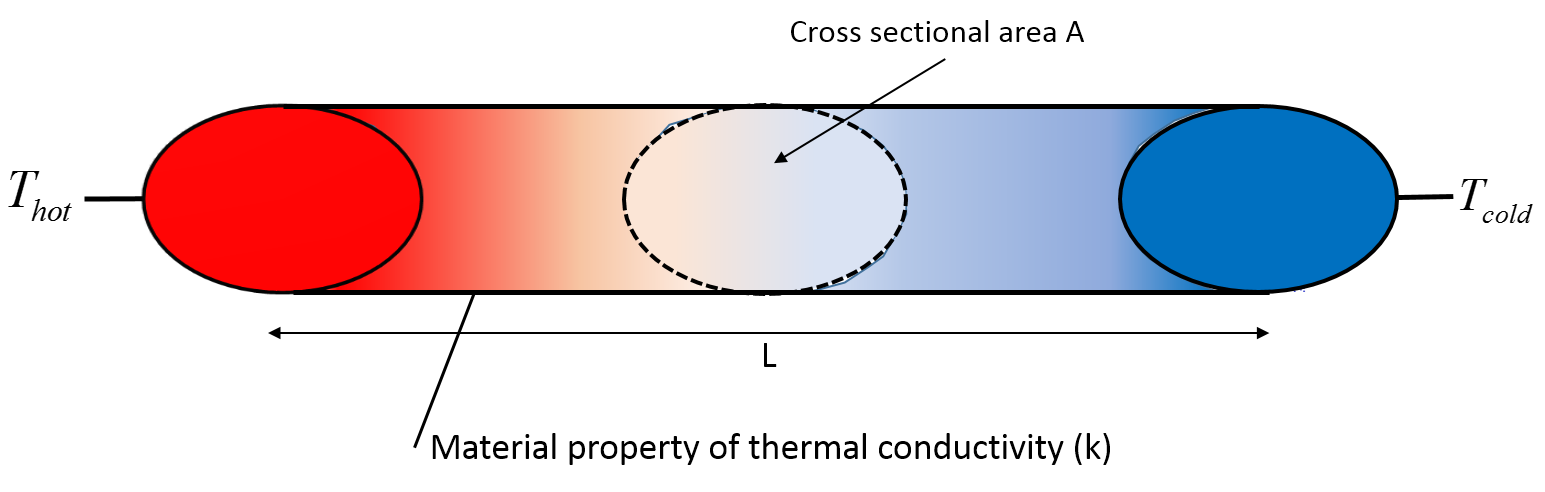
Conduction is quantified as a rate of energy per time. It is dependent on a number of factors including temperature differences, size parameters, and a material property called the thermal conductivity.
$\frac{Q}{\Delta t}=\frac{k A}{L} \Delta T$
Here $\frac{Q}{\Delta t}$ is the rate of energy transfer, measured in SI units as Joules per second. On the right-hand-side of the equation: k (kappa) is a material property called the thermal conductivity, A is the cross-sectional area through which the energy is being transferred, L is the length between the hot and cold side, and $\Delta T$ represents the temperature difference between the hot and cold side. In our discussion we will assume that the hot and cold sides stay at a constant temperature, making the situation in what's called Steady State - which simply means the rate of transfer is constant. An example is maintaining your house at 293 K while the outside maintains 278 K and energy is transfer through the window via conduction. Here A would be the area of the window, L would be the thickness of the glass, k you would look up for glass, and $\Delta T$ would be 293 K minus 278 K, or 15 K.
Convection: Thermal energy, which is a measure of motional energy of microscopic particles, can also be transferred when a higher energy particle physically moves from a higher energy to a lower energy location. In doing so they will have decreased the thermal energy in the hotter location and increased the thermal energy in the colder location. This physical transfer of mass from one location to another is called convection and is the most prevalent form of energy transfer in a gas.
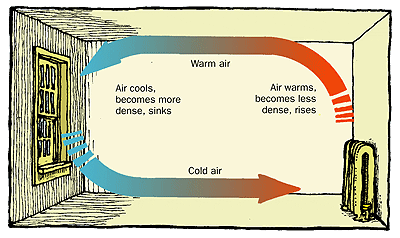
Quantifying convection requires the use of the calculus, which is beyond the scope of this discussion, so conceptual understanding is key. It's important to be able to identify when convection is present and describe the mechanism in terms of particles moving from one location to another.
Radiation: All objects with a temperature greater than 0 K, so all objects... even deep space is around 4 K, radiate electromagnetic energy.
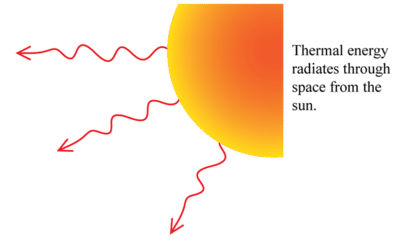
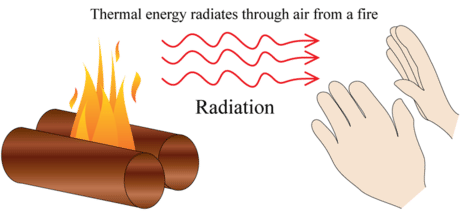
A full blown understanding of this phenomena requires deeper physics (quantum mechanics) than is the scope of our discussion here. But even if we can't understand all the underlying mechanisms, we can still quantify the results. As with conduction, radiation is cast in terms of a rate of energy transfer.
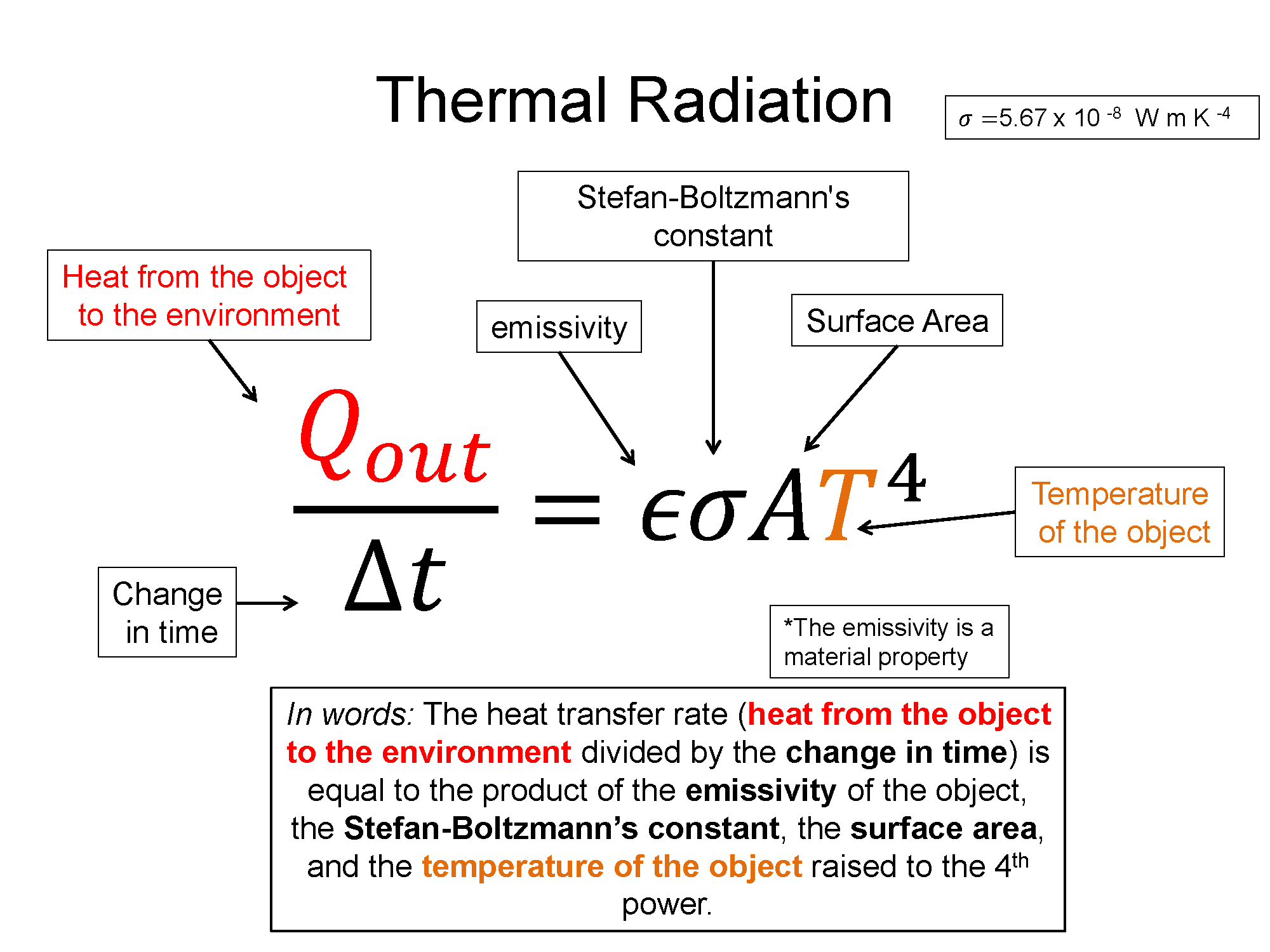
$\frac{Q_{out}}{\Delta t} = \epsilon \sigma A T^4$
In this equation $\epsilon$ is called the emissivity of the object and can be thought of as a material property. $\sigma$ is a constant called Stefan-Boltzmann's constant. A is the surface area of the object and T is the temperature of the object. It's important to note that T must be in Kelvin in this equation. Notice also that the equation says $Q_{out}$, that's because this is the radiation from the object to its environment. But what if the environment also has temperature, like it most definitely will? You must then account for what radiation also comes in to your system - you must find the net radiation in and out to get a complete picture of the change in energy per time. So, the net radiation looks like this:
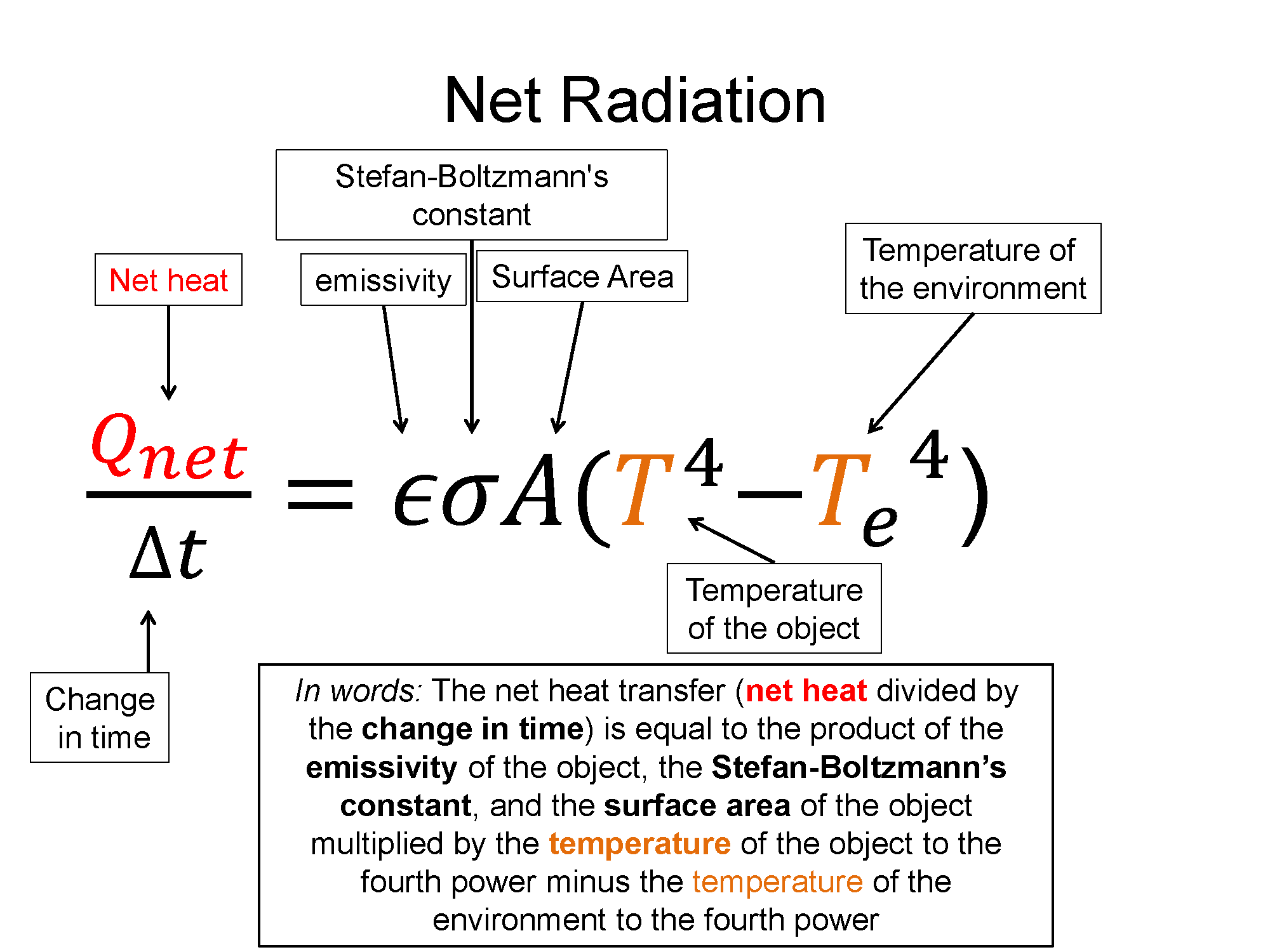
$\frac{Q_{net}}{\Delta t} = \epsilon \sigma A (T^4-T_e^4)$, where $T_e$ represents the temperature of the environment
Notice that if the object and its environment have the same temperature, the net thermal radiation is zero - just as much energy leaves as enters the object.
Key Equations and Infographics
Now, take a look at the pre-lecture reading and videos below.
BoxSand Videos
Required Videos
Suggested Supplemental Videos
none
OpenStax Reading
OpenStax Section 14.4 | Heat Transfer Methods
OpenStax Section 14.5 | Conduction
OpenStax Section 14.6 | Convection
OpenStax Section 14.7 | Radiation
Fundamental examples
1. Sally places a rod of copper with cross-sectional area $A=0.5 {cm}^2$ and length = $1m$ such that one end is touching hot coals at a temperature $T_H = 600K$ and the other is in a bucket of ice at $T_c = 273K$. What is the rate of heat transfer through the rod? What mechanism of heat transfer is this?
2. Sally removes the rod from the fire and uses a digital thermometer to read its temperature. A few seconds later, she measures the temperature again and realizes it has dropped. From this she infers that the rod is at a higher temperature than the room. Assuming the rod is a black-body radiator, what is the rate of heat transfer due to radiation if the rod is at a temperature of $T_{cu}=450 K$ and the room is at a temperature of $T_{room}= 300 K$?
3. Jimmy baked some pizza and now the inside of his oven is at 600 °F . He wans to cool it down to 325 °F so that he can bake some cupcakes. Jimmy thinks he should place a fan in front of the oven to help it cool down, but Jimmy's friend Tony says that, since the oven is at such a higher temperature than its environment (600 °F versus 70 °F in the room), thermal radiation will qiuckly cool down the oven. If the goal is to cool the oven as quickly as possible do you agree with Jimmy or Tony, and why?
Short foundation building questions, often used as clicker questions, can be found in the clicker questions repository for this subject.
Post-Lecture Study Resources
Use the supplemental resources below to support your post-lecture study.
Practice Problems
BoxSand's multiple select problems
BoxSand's quantitative problems
Recommended example practice problems
- Openstax problems are located towards the bottom of the page.
- 14.5 Conduction Website Link.
- 14.6 Convection Website Link.
- 14.7 Radiation Website Link.
- A good quiz to practice identifying heat transfer methods, Website Link
For additional practice problems and worked examples, visit the link below. If you've found example problems that you've used please help us out and submit them to the student contributed content section.
Additional Boxsand Study Resources
Additional BoxSand Study Resources
Learning Objectives
Summary
Summary
Atomistic Goals
Students will be able to...
YouTube Videos
Here is a nice a clear explanation of heat transfer by conduction, convection, and ratiadion.
Khan Academy uses a qualitative approach to explain conduction, convection, and radiation.
A nice video covering of the three methods of Heat Transfer, done by a couple of 8th graders!
A wonderful song(to the tune of Demons by Imagine Dragons) about Conduction, Convection and Radiation
Other Resources
This link will take you to the repository of other content related resources .
Simulations
This simulation will Help you visualize the different heat transfer methods.
For additional simulations on this subject, visit the simulations repository.
Demos
History
Oh no, we haven't been able to write up a history overview for this topic. If you'd like to contribute, contact the director of BoxSand, KC Walsh (walshke@oregonstate.edu).
Physics Fun
A wonderful song, to the tune of Demons by Imagine Dragons, about Conduction, Convection and Radiation
Other Resources
Resource Repository
The methods of Heat Transfer section on Boundless covers conduction, convection and radiation.
The Heat Transfer section of Hyperphysics also has their usual brand of concise information.
Physic Classroom's section which covers heat transfer methods.
This site gives a fairly compact view of heat transfer
Other Resources
This link will take you to the repository of other content related resources .
Problem Solving Guide
Use the Tips and Tricks below to support your post-lecture study.
Assumptions
Much like other areas of thermodynamics, our mathmatical models are approximations under very specific, but often broadly applicable, conditions. Our conduction equation falls apart if each separate part our system isn't in thermal equilibrium with itself for instance (i.e. it has specific hot or cold spots OR any variance in temperature beyond the conductive interface). Our radiation is based off a theoretical model called a blackbody, and while no true blackbodies exist in reality, the equation can get us reliable data from both hot iron cauldrens and distant stars! So these assumptions based on purely theoretical models can give a lot of useful data in the real world!
Checklist
For problems in this section, the crux of the problem is typically understanding which heat mechanism is involved, which means reading the prompt very carefully. There are certain key words and situations to look for:
- If a problem is discussing a solid object (a metal rod; a wooden floor) that is changing temperatures, it is likely a conduction problem.
- If a problem is talking about gas flow from one area to another (air conditioning; indoor heating), it is likely a convection problem.
- If a problem is discussing heat flow between seemingly disconnected systems (such as the Earth being isolated, via the vacuum of space, from our sun), it is likely a radiation problem.
Note that we only have quantitative equations for conduction and radiation, so any problems involving convection in this section will be qualitative (such as discussing the mechanism by which a space-heater is able to warm up a dorm room).
For conduction problems, you will use the equation
$\frac{Q}{\Delta t} = \frac{kA}{L}\Delta T$
where the left-hand-side is the rate of energy transfer, $A$ and $L$ are geometric terms (the cross-sectional area and length of the object in question), $\Delta T=T_f - T_i$, and $k$ is a constant. Take an inventory of which of these quantities you know and which you don't. You will typically be given the geometric terms, although sometimes they will be given in terms of something like a radius or diameter, in which case you'll have to do a quick calculation; remember that $\pi r^2 = \pi \left( \frac{d}{2} \right)^2 = A$ for circular cross-sections.
The equation that represents radiative heat transfer from one object to its environment is
$\frac{Q_{net}}{\Delta t}= \epsilon \sigma A T^4$
where $\epsilon$ and $\sigma$ are constants, $A$ the surface area of the object, and $T$ is the temperature of the object in question. Note that, while $A$ might be a cross-sectional area for conduction and a surface area for radiation, it serves the same purpose: in both cases, $A$ represents the surface or window through which thermal energy is being transferred.
For a lot of problems, you will be asked about the heat transfer between two systems, so the equation will look like $\frac{Q_{net}}{\Delta t}= \epsilon \sigma A (T_{1}^4 - T_{2}^4) $.
Misconceptions & Mistakes
Pro Tips
Notice in the equation for radiative heat transfer:
$\frac{Q_{net}}{\Delta t} = \epsilon \sigma A(T^4 - T_{e}^4)$
the temperatures of the system and environment are individually cubed before you find the difference between the two values. Do not make the mistake of thinking that $T_{1}^4 - T_{2} ^4 = (T_1 - T_2) ^4$. If you're not convinced, plug in some sample numbers and try to convince yourself, or try expanding out each term the same way you would expand out $(a - b)^2$.
Note that, while $A$ might be a cross-sectional area for conduction and a surface area for radiation, it serves the same purpose: in both cases, $A$ represents the surface or window through which thermal energy is being transferred.
Multiple Representations
Multiple Representations is the concept that a physical phenomena can be expressed in different ways.
Physical
We have a tube where one end is in a hot water bath and the other in a cold water bath.
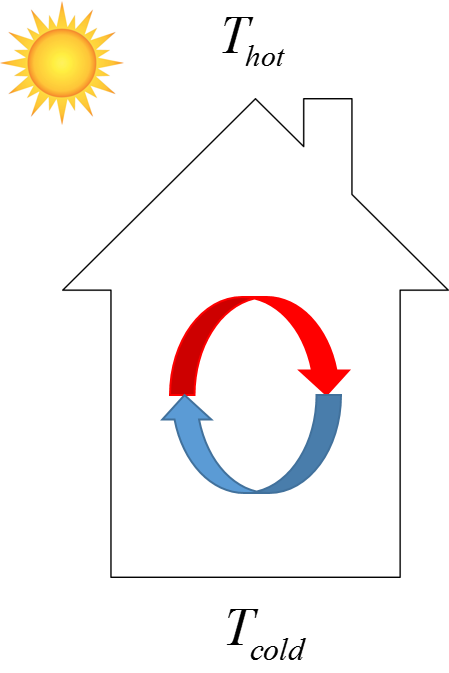
Convection
Heat from the sun is the hot reservoir and the earth that the house sits on is the cold reservoir. The difference in the two hot and cold reservoirs is a perfect system for convection.
Radiation
Radiation from a hot object such as the sun.
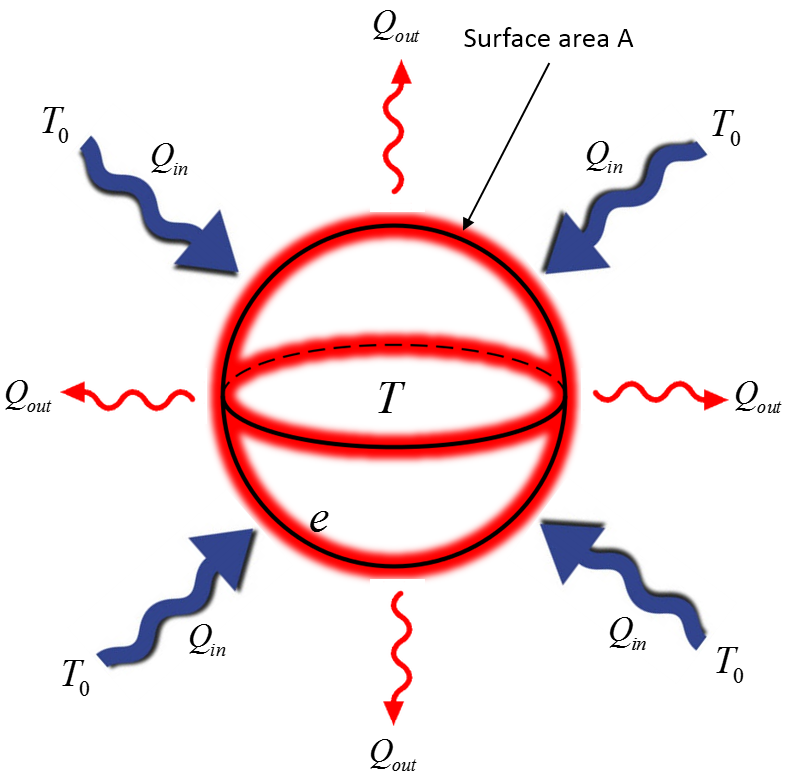
Mathematical
Conduction
$\frac{Q}{\Delta t} = \frac{kA}{L} \Delta t$
$\frac{Q}{\Delta t} \implies \frac{Energy}{time}$
Convection
Mathematical Representation for Convection is complicated...
Radiation
$\frac{Q_{out}}{\Delta t} = e \sigma A T^{4}$, Radiation out
$\frac{Q_{in}}{\Delta t} = e \sigma A T_{0}^{4}$, Radiation in
$\frac{\sum Q}{\Delta t} = e \sigma A (T^{4}-T_{0}^{4})$, Net radiation



Graphical
Conduction
Molecules on the hot side of the are moving (vibrating) more than they are on the cold side. This motional energy propagates down the material via collisions with adjacent molecules. One molecule vibrates the next molecule which then vibrates the next and so on.
Convection
Faster moving hot molecules move to the slower moving cold side, increasing the average kinetic energy. This action may cause cold molecules to be pushed to the hot side creating convection currents.
Radiation
Thermal radiation consists of electromagnetic waves that carry energy away from the sources and transfer the energy to another object. A perfect example is the sun. The energy transfer to your skin via electromagnetic waves may be felt by your skin warming up.
Descriptive
Experimental
Conduction
Here we have an experiment that demonstrates conductivity.
Convection
Here we have an experiment that demonstrates convection.
Radiation
We can take an ice cube and set it out in the sun to observe thermal radiation. The electromagnetic waves from the sun transfer energy from the sun to the ice cube, which increases the temperature of the ice cube thus melting the ice.