We dedicated a section with the title Heat to cover the concepts of a material property called Specific Heat and Latent Heat of Transformation, along with the experimental tool called Calorimetry. Specific heat is a measure of how much energy (per mass) must be exchanged to change the temperature of a substance a certain amount. Latent heat of transformation is a measure of how much energy (per mass) must be exchanged to take a substance over a phase transition, like from a liquid to a solid. Calorimetry is a technique to put different substances together in an isolated (no exchange of energy with the environment) container, and use their transfer of energies between each other, to determine the final equilibrium temperature of the system or to measure specific heats of one of the substances.
Pre-lecture Study Resources
Watch the pre-lecture videos and read through the OpenStax text before doing the pre-lecture homework or attending class.
BoxSand Introduction
Thermo | Specific Heat, Phase Transformations, Calorimetry
The section is dedicated to Specific Heat, Latent Heat of Transformation, and the experimental technique of Calorimetry.
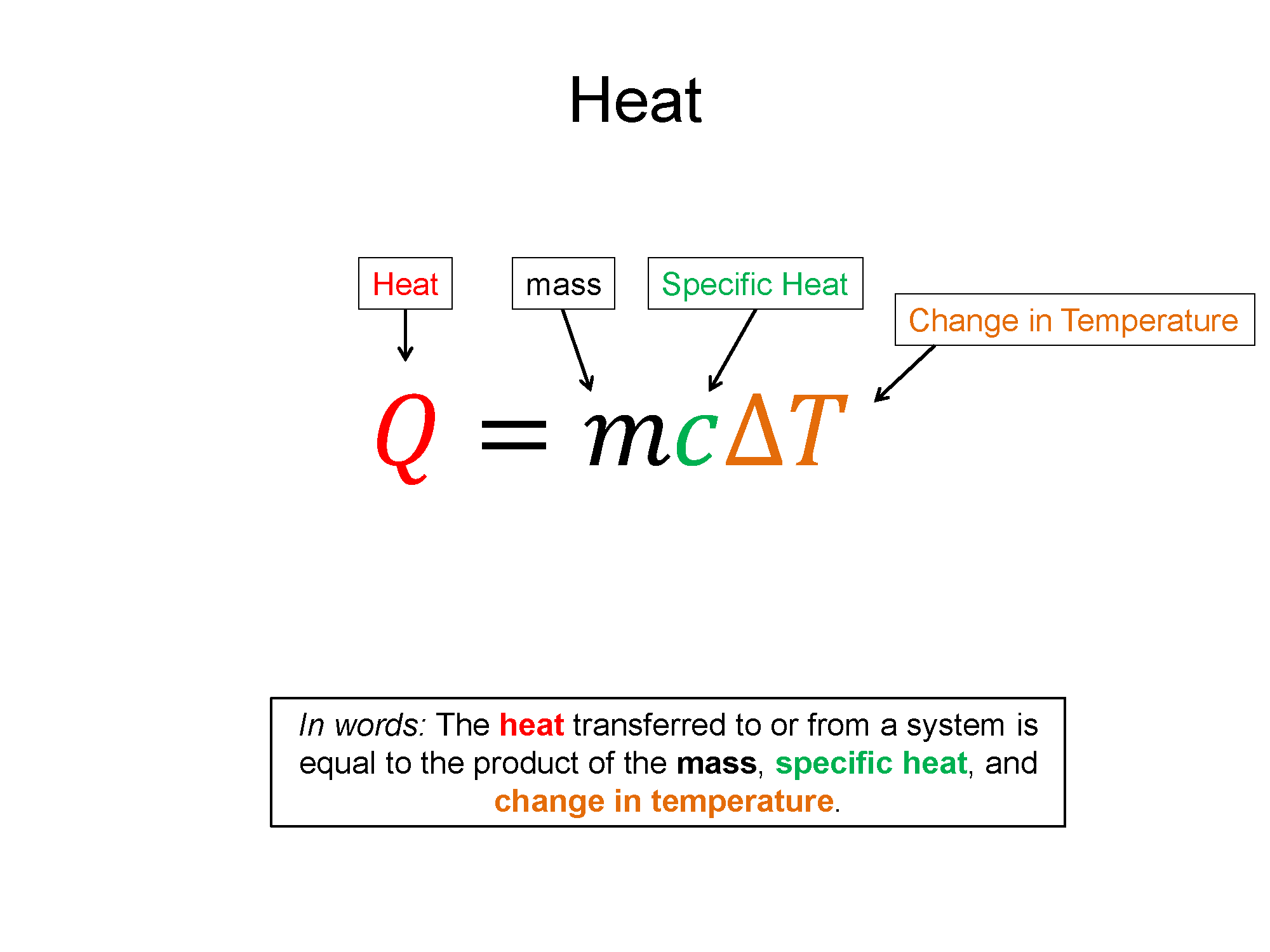
Specific Heat: To increase the temperature of a substance you must add energy. Specific heat (c) is a measure of how much energy (per mass) is required to change a substance a certain temperature, while remaining in a given state (e.g. a liquid).
$c=\frac{1}{m}\frac{\Delta E}{\Delta T}$
The specific heat is a material property since every equal mass substance, when introduced with the same amount of increased energy, would display a different change in temperature. Since energy in these types of experiments is rarely exchanged via work, the form of energy transfer is usually just heat and $\Delta E = Q + W$ reduces to $\Delta E = Q$. With this assumption and a rearrangement of the equation, you get form more often seen in Chemistry. The noted Q equals M C delta T equation.
$Q=mc\Delta T$
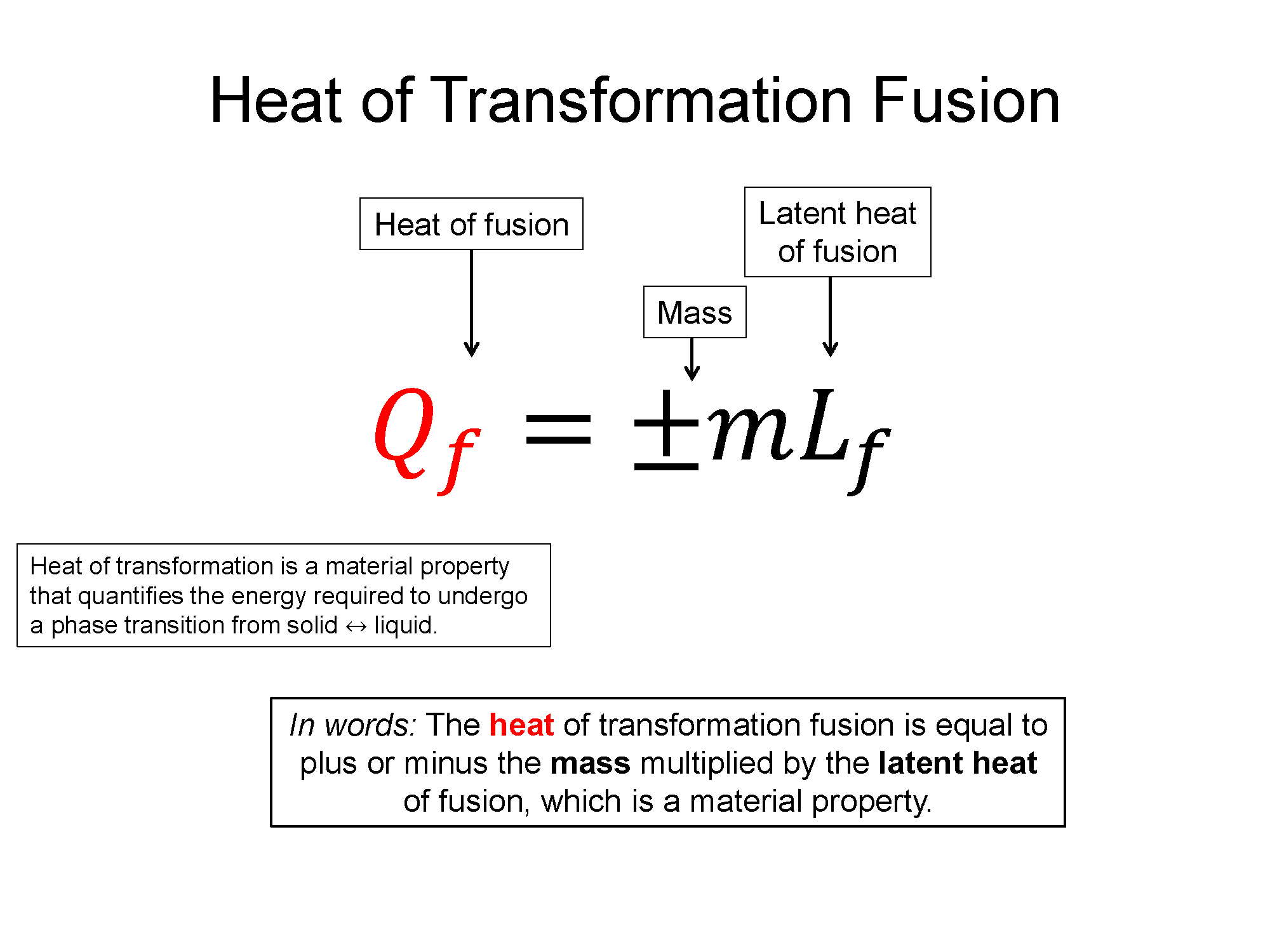
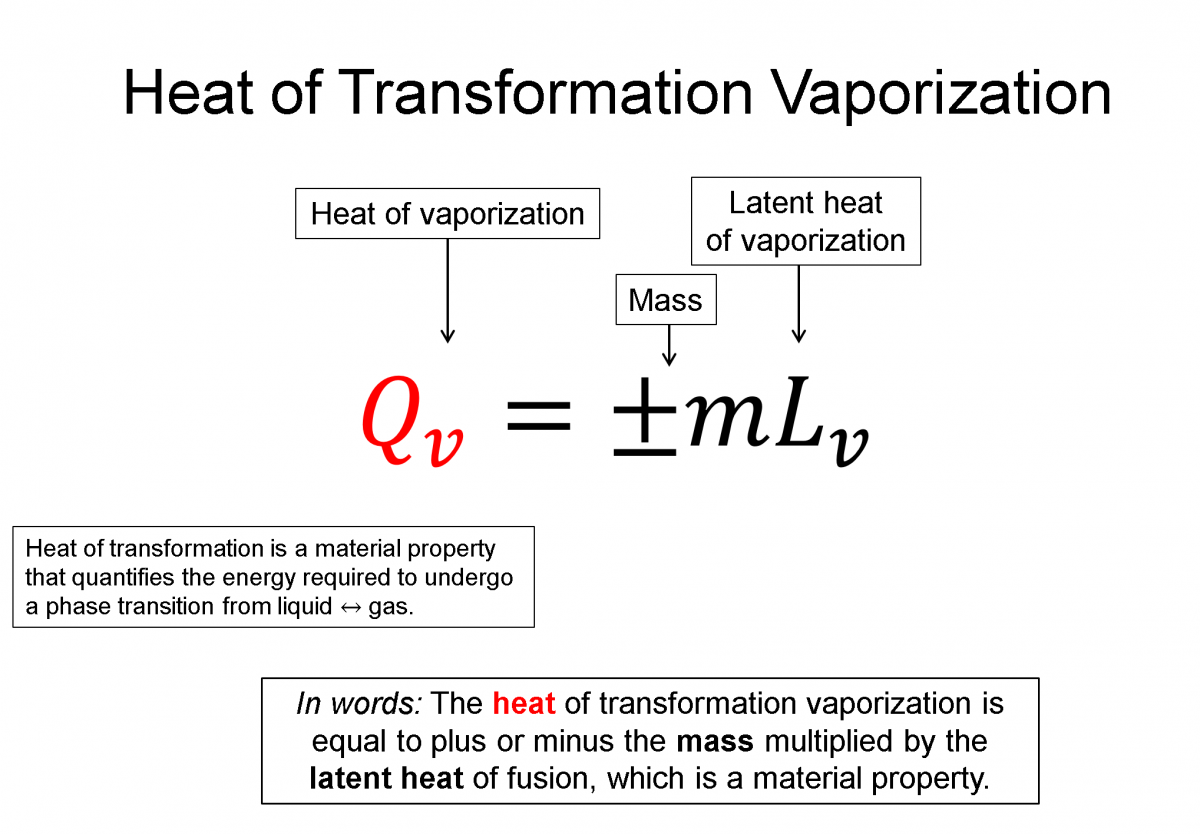
Latent Heat of Transformation: If you where to place a thermometer in a sealed container of very cold (-20 C) ice and heated that container up, you'd see that temperature would increase until it reached 0 C, where while still in solid form, it would begin to change phase into a liquid. This phase transformation from a solid (ice) to a liquid (water) takes time and during that time the system is still increasing its energy, but the temperature doesn't change until all the ice has transformed to water. What this experiment tells you is that it takes energy to change the phase of the system but the temperature does not chance during that transition. Microscopically this means you must put energy into the system to break the bonds holding the molecules tightly together in the solid form, but that energy only goes into the phase transformation and not into the microscopic kinetic energy (temperature). Heat of transformation is a quantification of this energy required to go across a phase transition and it is also a property of the material.
Heat of Fusion (solid <=> liquid), $Q_f = \pm m L_f$
Heat of Vaporization (liquid <=> gas), $Q_v = \pm m L_v$
Here Lf and Lv are transformation properties of the material and the +/- is chosen by whether it's a liquid to gas or a gas to liquid transform.
Calorimetry: A non-SI unit for energy is the Calorie and that is the root of the term calorimetry. Calorimetry is an application of conservation of energy. Calorimetry experiments involve putting two (or more) substances in an isolated container. Isolated means they cannot exchange any energy with the environment, but that can exchange energy between each other. Heat will transfer from the hotter substance to the colder substance until the two reach equilibrium, somewhere in between their initial temperatures. Since the total change of energy of the system must be zero, we can setup an energy expression using the energy transfers during a single phase ($Q=mc\Delta T)$ and the energy transfer for any phase transitions ($Q_f$ or $Q_v$).
$\sum Q = 0$, or $Q_1+Q_2+... = 0$
An example might be putting a hot stone into water and after equilibrium, the whole system is warmer but no steam was generated. Here there are no phase transitions so the $mc\Delta T$ of the stone must be equal and opposite to the $mc \Delta T$ of the water.
$Q_{stone}+Q_{water} = 0$, or $(mc\Delta T)_{stone}+(mc \Delta T)_{water}=0$
Now if the stone had been hot enough to not only increase the water temp up to the boiling point but also turn it into steam, there would an additional term for the phase transition of the water.
$Q_{stone}+Q_{water}+Q_{v,water} = 0$, or $(mc\Delta T)_{stone}+(mc \Delta T)_{water}+(mL_v)_{v, water}=0$
This expression could be used to find the specific heat of the stone, if initial and final temps as well as the mass and specific heat of the water was known. I use this in brewing to calculate what the final temperature of hot water mixed with cold grains will be so that I get the desired final temp.
Key Equations and Infographics

Now, take a look at the pre-lecture reading and videos below.
BoxSand Videos
Required Videos
Suggested Supplemental Videos
OpenStax Reading
OpenStax Section 14.1 | Heat
OpenStax Section 14.2 | Temperature Change and Heat Capacity
OpenStax Section 14.3 | Phase Change and Latent Heat
Fundamental examples
1. The specific heat of Aluminum is $ c_{Al} = 900 \frac{J}{kg \cdot K}$. You have 500 g of aluminum and you want to raise its temperature from 20 degrees Celsius to 40 degrees Celsius. How much thermal energy must be added to the system?
2. You’re making some tea for your granny, and you remember that she likes having her tea at a cool 80 degrees Celsius. You’ve steeped the tea, and now you fill 80% of your granny’s 500 mL teacup with 100 degree Celsius tea-water. What is the minimum mass of ice you should add to cool her tea? Assume the specific heat $c$ of tea-water is the same as regular water, and assume no other cooling processes take place while the ice melts.
3. <Calorimetry question>
Short foundation building questions, often used as clicker questions, can be found in the clicker questions repository for this subject.
Post-Lecture Study Resources
Use the supplemental resources below to support your post-lecture study.
Practice Problems
BoxSand's multiple select problems
BoxSand's quantitative problems
Recommended example practice problems
- Openstax exercises are found at the bottom of the page,
- 14.1 Heat - Three conceptual problems, Website Link
- 14.2 Heat Capacity/Specific Heat/Phase Change - Two conceptual problems, 10 practice exercies. Website Link
- A PDF with a huge number of questions on the subject. PDF Link
For additional practice problems and worked examples, visit the link below. If you've found example problems that you've used please help us out and submit them to the student contributed content section.
Additional Boxsand Study Resources
Additional BoxSand Study Resources
Learning Objectives
Summary
Summary
Atomistic Goals
Students will be able to...
YouTube Videos
Crash Course Chemistry discusses the Physics of Heat, also talks about specific heat and phase changes and latent heat!
Doc Schuster gives a nice brief on drawing Phase Diagrams.
The doc does an example including Latent Heat, Phase Change and Heat Capacity.
As a preview for the section on the second law of thermodynamics, this musical bit will help you remember the direction of energy transfer as heat.
Other Resources
This link will take you to the repository of other content related resources .
Simulations
This mini lab simulation has the student melt ice, collect data points, then plotting the data.
For additional simulations on this subject, visit the simulations repository.
Demos
History
Oh no, we haven't been able to write up a history overview for this topic. If you'd like to contribute, contact the director of BoxSand, KC Walsh (walshke@oregonstate.edu).
Physics Fun
https://www.youtube.com/embed/tj7S_DNFgEU?rel=0
Check out the example below where a balloon doesn't pop when exposed to a flame if it has some water inside.
Other Resources
Resource Repository
Boundless also has a large section that covers heat, heat capacity, specific heat and calorimetry. Take a look at sections one through three. Section four will be used later on.
Hyperphysics provides a decent amount of information pertaining to Heat, it's mechanical equivalent, and several examples.
| Heat | Specific Heat |
| Calorimetry | Phase Change |
Physics classroom looks at the question, "What is heat" and then looks at how heat can be measured and it's effects on matter
| Heat | Specific Heat, Phase Change, Heat Capacity |
This link will take you to the repository of other content related resources.
Problem Solving Guide
Use the Tips and Tricks below to support your post-lecture study.
Assumptions
The core assumptions made in calorimetry is that we're dealing with an isolated system in a rigid container (no outside heat gets in, and no work is done via an expanding or contracting gas or liquid). However, the biggest assumptions in problem solving these problems is what we assume the system is doing. Specifically, when is it changing temperature and when is it going through a phase change, since those are the two different types of heat equations we have to use.
Remember, Q=m*c*DeltaT is for CHANGING temperature (the DeltaT tells you this!). Heat for a phase transition is Q=m*L (use the L for fusion for freezing/melting, vaporization for condensing/boiling). Systems DO NOT change temperature when they're changing phase (changing between solid, liquid, and gas), all the energy that would normally go into changing the temperature go up goes into changing phase of matter the substance is in. After it is finished changing, the substance can then resume changing temperature.
Keep in mind important turning points for common substances like water, 0C for freezing, 100C for boiling. These will often not be mentioned in the question statement and you'll have to make the assumptions of what the water is and what it is doing when heated or cooled at various temperatures.
Checklist
General problems
Since heat is a mechanism for transferring thermal energy between systems, expect some heat problems to really be problems about changes in $E_{th}$ according to the First Law. In the previous section you were typically given 2 of the variables out of $Q$, $W$, and $\Delta E$ and asked to calculate the other. In this section you will mostly be using the following two equations:
$Q_f = \pm mL_{f,v}$
or
$Q=mc\Delta T$
In general, you will be given a few variables and asked to solve for another - such as being given a mass, heat capacity, and change in temperature of an object, and asked how much thermal energy was transferred into our out of the object as heat. Or, you may be asked, for a given type of object, how much its temperature would change when in contact with a thermal reservoir that transfers some $Q_H$ amount of heat. For most of these problems, read the prompt carefully and take an inventory of your knowns and unknowns and the rest should be straightforward. Being able to do this comfortably will help enormously with calorimetry problems.
Calorimetry
Remember that calorimetry specifically refers to isolated systems with constant volume, so both the change in thermal energy of the system and work done on or by the system is zero ($ \Delta E = W = 0$).
1. For all calorimetry problems, begin by summing the heat flow in into and out of the system:
$\Sigma Q = Q_1 + Q_2 + Q_3 + ... = 0$
2. After summing the sources of heat flow, read the problem statement again and verify that you haven't missed any sources (this is a common mistake students make - misreading a problem and missing that there is a phase change, for example).
3. Re-write the sum in terms of definitions. For each $Q$, plug in its $mc\Delta T$. If phase changes are present and thus you have heats of transformation present, replace $Q$ with $mL_v$ or $mL_f$ with $v$ for vaporization, $f$ for fusion.
For example, pretend you put a hot rock in a container of liquid water and you observe steam. The equation to describe this is
$\Sigma Q = Q_{rock} + Q_{water,l} \pm Q_{v,water} + Q_{water,g}$
which is re-written as
$\Sigma Q = m_{r}c_{r}\Delta T_{r} + m_{w,l}c_{w,l} \Delta T_{w,l} + m_{v,w} L_{v, w} + m_{w,g}c_{w,g}\Delta T_{w,g}$
*The $\pm$ in front of the heat of vaporization term in the first equation was replaced by a $+$ sign in the second equation because we know the transformation was from liquid to vapor, and that is the sign convention for such a phase transition.
4. This equation should include all of the information you need to solve the problem. Note that since the systems are in thermal contact, they will come to thermal equilibrium and thus have the same final temperature $T_f$, but not the same $\Delta T$.
Often the point of a calorimetry problem is to find a final temperature, although sometimes the final temperature is given and you are asked for the heat exchange between particular sub-systems (such as the amount of thermal energy required to produce as much steam as was observed). Remember that the final temperature should be somewhere between the initial temperatures of the sub-systems (liquid water and hot rock); if it is somewhere outside, you probably made a calculation mistake or have a sign error somewhere (check that your $\Delta T = T_f - T_i$ have the correct signs).
Misconceptions & Mistakes
- Heat is a mechanism by which thermal energy is transferred between systems. A system does not "contain" heat - it is not a state variable like P, V, T, N (and S).
- Note that just because a phase change is taking place doesn't mean $W=0$; you can change liquid water to steam by changing the pressure of its container.
Pro Tips
- Practice practice practice. This section looks like a giant hair ball at first (especially calorimetry questions), but ends up being straightforward if you are careful and take your time. You will have lots of variables to keep track of (and lots of them are $Q_{something}$), so the more you practice keeping track of them, the easier your life will be.
Multiple Representations
Multiple Representations is the concept that a physical phenomena can be expressed in different ways.
Physical
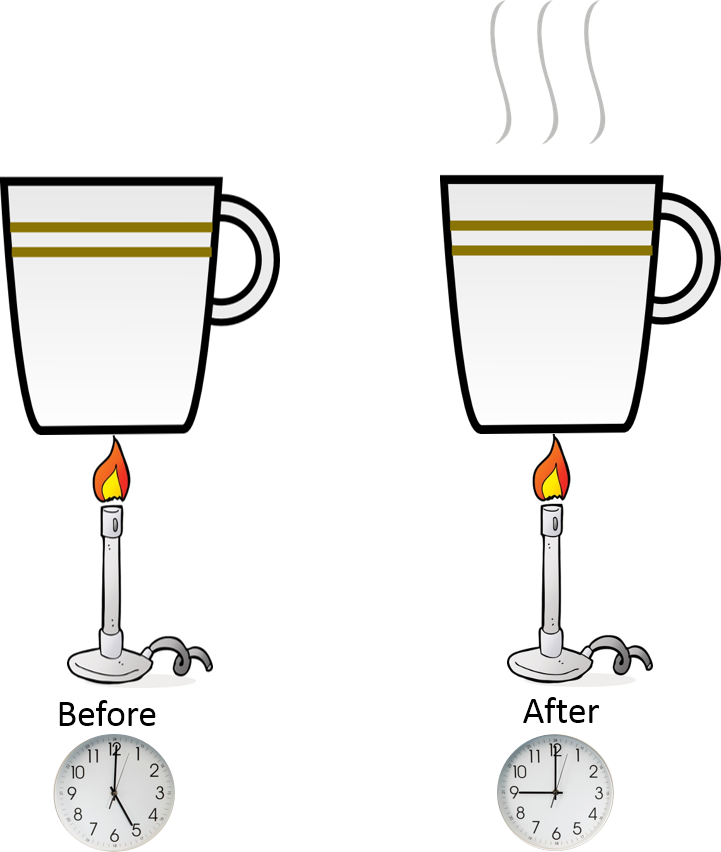
Heat transfer occurs from the flame to the water in the cup. It takes energy through heat transfer to change the temperature of the water in the cup. As we add heat to the system the energy increases with respect to time.
Mathematical
$Q = mc\Delta t$, where c is specific heat
$Q = \pm mL_{f,v}$, where L is latent heat
Calorimetry if all the transfer occurs in an isolated system, then we have the following:
$\Delta Q_{tot} = 0$ then $\sum Q = 0 \implies Q_1 + Q_2+Q_3 ... Q_n =0$




Graphical
The graph describes the general phase transitions for a material. Notice the transition phases from solid to liquid and liquid to gas are constant temperature. Different materials have different temperature values where the phase transition occurs.
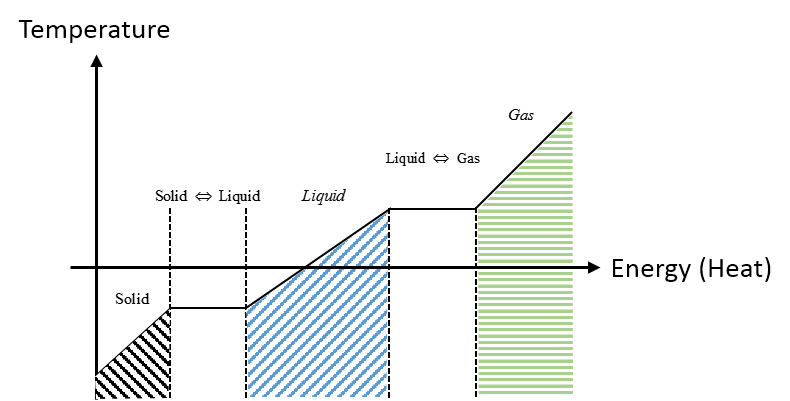
Descriptive
Referring to the Graphical Representation that describes the phase transitions of a material. During the initial solid phase the temperature increases and we add energy to the system until we reach the first phase change where we have reach the temperature required for the material to undergo the first phase transition. The next phase is the liquid to solid transition, where the material requires more added energy to the system to raise the temperature and complete the last phase transition.
Experimental
We can begin with an ice cube, a closed lid cup, a thermometer, and a bunsen burner. We place the ice cube inside the cup and insert the thermometer and close the lid around the thermometers. Place the the cup over the bunsen burner and ignite the flame. Record the temperature and observe the state of the matter. We can then use this information to plot a phase change diagram as depicted in the Graphical representation and observe the temperature as it relates to the energy required for the ice to undergo transitions from ice to water to gas.