In this section we will explore Archimedes principle which relates an upward force acting on an object that is fully or partially submerged within a fluid to the weight of the fluid that the object displaces. We will also build upon our understanding of density, pressure, and hydrostatics to quantify the buoyant force.
Do you ever woder why you don't sink to the bottom of the pool or ocean? Check out this OpenStax concept trailer to find out.
Pre-lecture Study Resources
Watch the pre-lecture videos and read through the OpenStax text before doing the pre-lecture homework or attending class.
BoxSand Introduction
Fluid Statics | Hydraulics Pressure and Buoyancy
Hydraulics
Consider the analysis we did in the "pressure at a depth" section. If the pressure $P_0$ above the surface of the water increases by some amount $\Delta P$ so that the new pressure above the surface is now $P^{'}_{0} = P_0 + \Delta P$, then the pressure at all locations within the fluid also increase by the same amount $\Delta P$. Thus the pressure at the bottom of the volume element would be $P_1 + \Delta P = P_0 + \rho_{f} \, g \, d + \Delta P$.
Hydraulic brakes and lifts generally work by applying a force over an area at one location which increases the pressure at that location along with all other locations in the system. Thus hydraulics are an interesting application of Pascal's law. Below is a figure illustrating a simplified hydraulic lift.
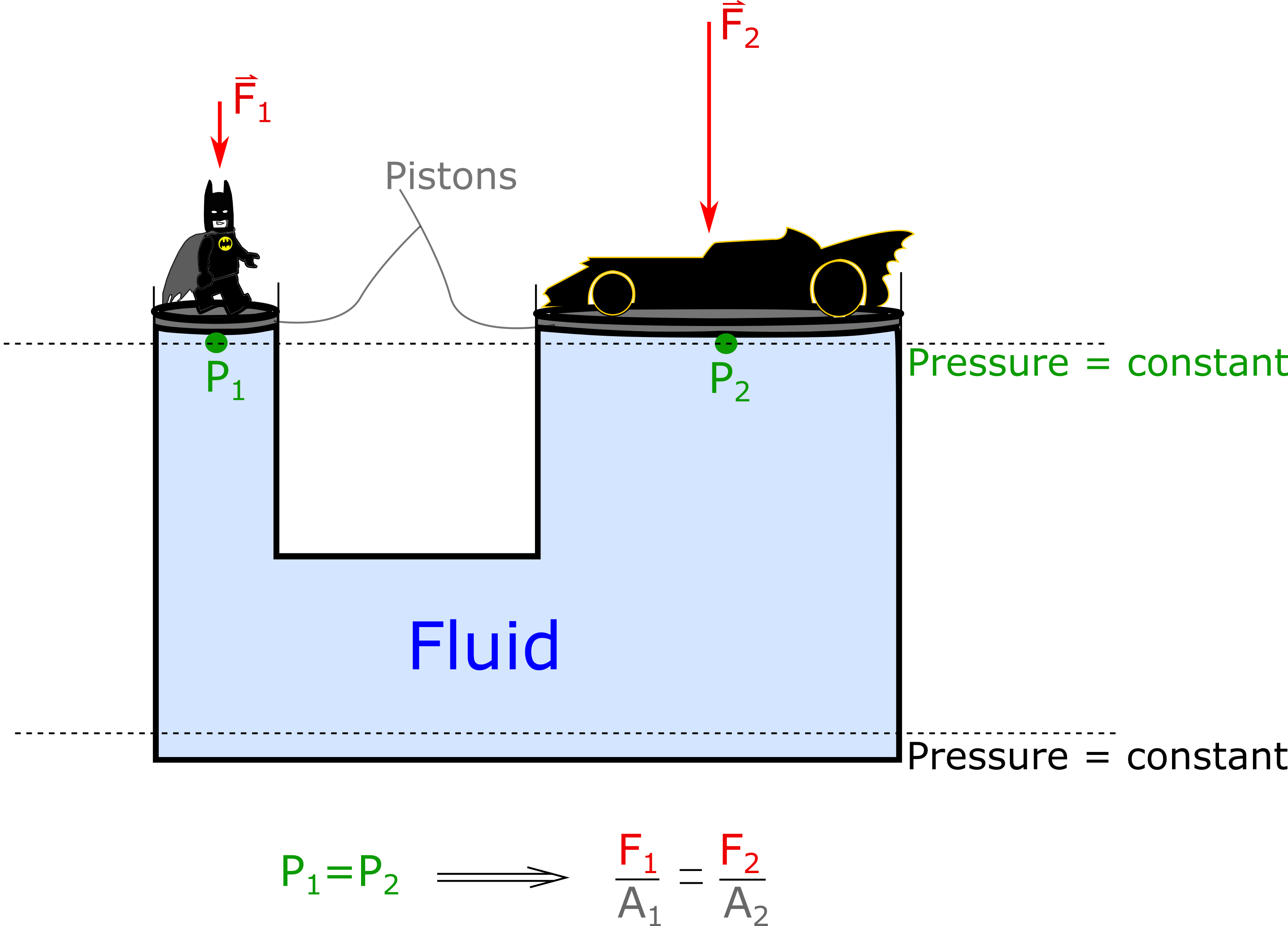
Did you ever notice that lifting a partially or fully submerged object in water feels easier to do than lifting the same object when it is outside the water? This effect is a consequence of the pressure gradient that the object experiences when in the water. Recall that pressure gradients cause an associated net force. The net forced caused by a pressure gradient within a fluid is what we refer to as the buoyant force, and it points in the upward direction which is why it feels easier to lift objects in water.
Buoyancy (Archimedes' Principle)
The discovery of how the buoyant force can be related other physical quantities is attributed to Archimedes. Archimedes’ principle can be stated as “when an object is partially or fully submerged in a fluid which is at rest, the pressure gradient within the fluid causes an associated net force in the upwards direction which is equal to the weight of the fluid that the object displaced”. Below is a physical representation to help illustrate Archimedes’ principle which was stated in the descriptive representation above.
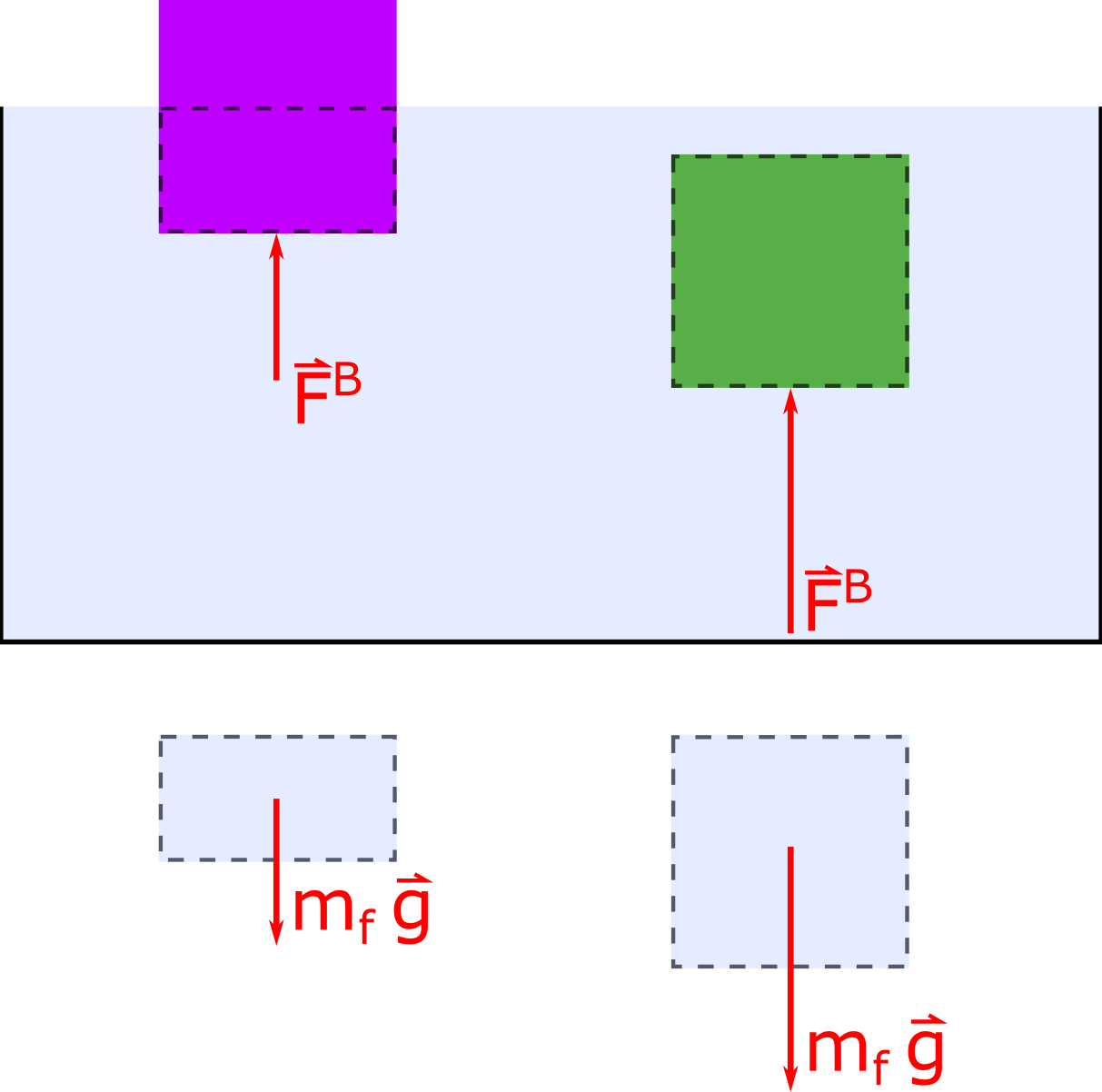
Notice that both the purple and green objects have the same dimensions, thus the same volume. However, the purple object is displacing a smaller volume of water than the green object. The volume of water that each object is displacing is shown below the container. Archimedes’ principle tells us that the buoyant force that each object experiences is equal to the weight of the displaced fluid, thus the green object experiences a larger buoyant force.
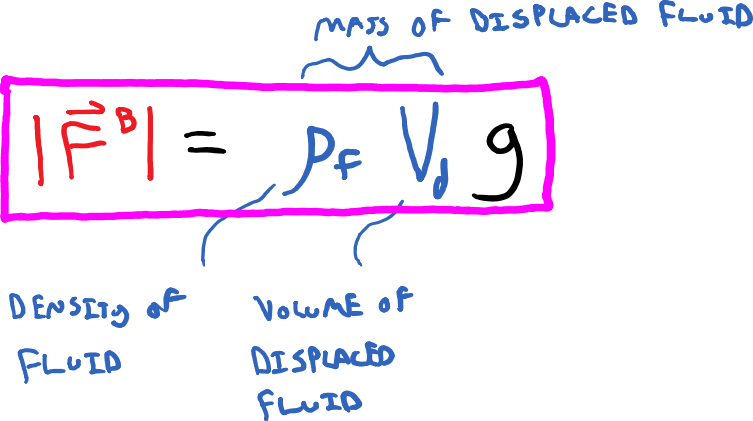
We can now quantify the buoyant force that any object experiences when either partially or fully submerged in a fluid as shown in the equation below.

However it is often much easier to work with volumes and densities instead of mass, so if we use our definition for mass, m = rho V and substitute this into the equation above, we get a much more handy expression for the magnitude of the buoyant force as seen below.
If you consider an object fully submerged in a fluid and apply Newton’s laws of motion, you can construct the conditions that must be satisfied for an object to sink or float. The conditions for sinking or floating are as follows...
if $\bar{\rho}_{object} > \rho_{fluid}$ , object sinks
if $\bar{\rho}_{object} < \rho_{fluid}$ , object floats
if $\bar{\rho}_{object} = \rho_{fluid}$ , neutrally buoyant
...where the bar over the object density indicates that it is the average density of the object.
Key Equations and Infographics

Now, take a look at the pre-lecture reading and videos below.
BoxSand Videos
OpenStax Reading
Fundamental examples
1. The largest gold bar easily available for an individual to purchase has dimensions of about $3.15$ inches by $1.58$ inches by $0.71$ inches ( length x width x height). What is the mass of this gold bar? The density of gold is about $19,320 \, kg / m^3$.
2. Your goal is to make 12 gauge copper speaker wire (cylindrical cable with a diameter of about $2.05232 \, mm$. What is the length of wire you can produce if you start with $0.5 \, kg$ of copper?
CLICK HERE for solutions.
Short foundation building questions, often used as clicker questions, can be found in the clicker questions repository for this subject.
Post-Lecture Study Resources
Use the supplemental resources below to support your post-lecture study.
Practice Problems
BoxSand Practice Problems (SOLUTIONS)
Conceptual problems
BoxSand's multiple select problems
BoxSand's quantitative problems
Recommended example practice problems
- Openstax section on density has practice problems at the bottom, Website Link
- 8 problems, strictly density, PDF Link
For additional practice problems and worked examples, visit the link below. If you've found example problems that you've used please help us out and submit them to the student contributed content section.
Additional Boxsand Study Resources
Additional BoxSand Study Resources
Learning Objectives
Summary
Summary from OneNote
Atomistic Goals
Students will be able to...
Hydraulics
1. Apply pressure at a depth principles while solving problems.
2. Relate Pascal's Law to hydraulic applications.
3. Identify mechanical advantage in hydraulic systems.
4. Construct FBDs and e-FBDs in parallel with a hydrostatics analysis to analyze systems.
Bouyancy
5. Understand that the buoyant force is a result of a pressure gradient within a fluid.
6. Demonstrate the ability to analyze a scenario involving a buoyant force by constructing FBDs and applying Newton's laws of motion.
7. Strengthen the ability to perform proportional reasoning.
YouTube Videos
Simulations
Demos
Check out this anvil floating in mercury
For additional demos involving this subject, visit the demo repository
History
Oh no, we haven't been able to write up a history overview for this topic. If you'd like to contribute, contact the director of BoxSand, KC Walsh (walshke@oregonstate.edu).
Physics Fun
Oh no, we haven't been able to post any fun stuff for this topic yet. If you have any fun physics videos or webpages for this topic, send them to the director of BoxSand, KC Walsh (walshke@oregonstate.edu).
Other Resources
Boundess sections on variation of pressure with depth
and gauge pressure
Hyperphysics section on Pascal's Principle and hydraulic press.
Boundless covers buoyancy throughout their section on the Archimedes principle
Hyperphysics covers buoyancy and the Archimedes principle
Resource Repository
This link will take you to the repository of other content related resources .
Problem Solving Guide
Use the Tips and Tricks below to support your post-lecture study.
Assumptions
When working we fluids, we typically assume incompressibility, which means that the fluid doesn't compress at all under pressure. This is a good approximation for many fluids, including water. A consequence of this is that if pressure is exerted on a fluid (say with a piston) it will push in every direction with equal pressure to that exerted on it.
As also assume the fluid has no internal resistance to movement (viscosity), the molecules have no interaction with each other, and neglect many aspects that typically concern practice applications of fluids like surface tension, eddy currents, energy and force lost to rotating liquid molecules. The study of fluid mechanics is highly complicated because there are a lot of different and not easily defined properties to fluids that aren't as much of a problem when studying gases or solids.
Most aspects of fluid dynamics are beyond the scope of this course and fully realized descriptions of how fluids move and work in the real world can usually only be approximated through computer simulations given that their movement is highly non-ideal and difficult to do regular calculations with. With this in mind, we restrict our discussion of fluids to focus on macro aspects of fluids, such as volume and pressure, and make idealizing assumptions, that turn out to be pretty accurate for most fluids, freely that make them analytical. While this aspect is true for most areas of physics we have studied, for fluids it is more true than ever.
Checklist
1. Read and re-read the whole problem carefully.
2. Visualize the scenario. Mentally try to understand what the problem is asking (think about the geometry, such as cylinders, cubes, spheres, etc.. that the problem might be asking about).
3. Draw a physical representation of the scenario, this may include a picture of an object with labeled dimensions.
4. Identify all the knowns and unknowns.
5.a. Start with the definition of mass density $\rho = \frac{m}{V}$. OR
5.b. Start with the definition of pressure $P = \frac{F_{\perp}}{A}$.
a. Identify which quantities you know and don't know.
b. Use the geometry of the object and subsitute the definition of volume for that specific shape if necessary.
6. Carry out the algebraic process of solving the equation.
7. Evaluate your answer, make sure the units are correct and the results are within reason.
Misconceptions & Mistakes
- Densities are often given in terms of $g/cm^3$. Be careful when looking up these values. It is recommended to always use SI units ($kg, m, s$).
- The density of materials can change, but solids and liquids change by vary small amounts thus we ignore these changes and assume that the densities are constant for a wide range of pressures and temperatures.
- Since we only use the perpendicular component of force, pressure is a scalar. Be sure to only use the perpendicular component of force.
- Absolute pressure can not be negative, but gauge pressure can be negative.
- The net force due to a pressure gradient is not the overall net force of an object, there may be other forces acting on the object you must account for.
Pro Tips
- When trying to find the volume, mass, or density of an object, draw a picture of that object and label all dimensions. This will help you visualize the geometry of the problem.
- When trying to find the volume, mass, or density of an object, draw a picture of that object and label all dimensions. This will help you visualize the geometry of the problem.
Multiple Representations
Multiple Representations is the concept that a physical phenomena can be expressed in different ways.
Physical
Since there are more particles in the left box, the density inside the left box is higher.
The change in velocity is of a particle is directly proportional to the force. We have a partilce that collides with a wall. The force on the particle due to the impact is equal and opposite. Imagine the wall bleow is part of a container, the higher the velocity of the impacting particle the greater the force. In turn this means a higher pressure inside the container.
Mathematical
$\rho = \frac{m}{V}$
Volume mass density ($\rho$), Mass ($m$), Volume ($V$)
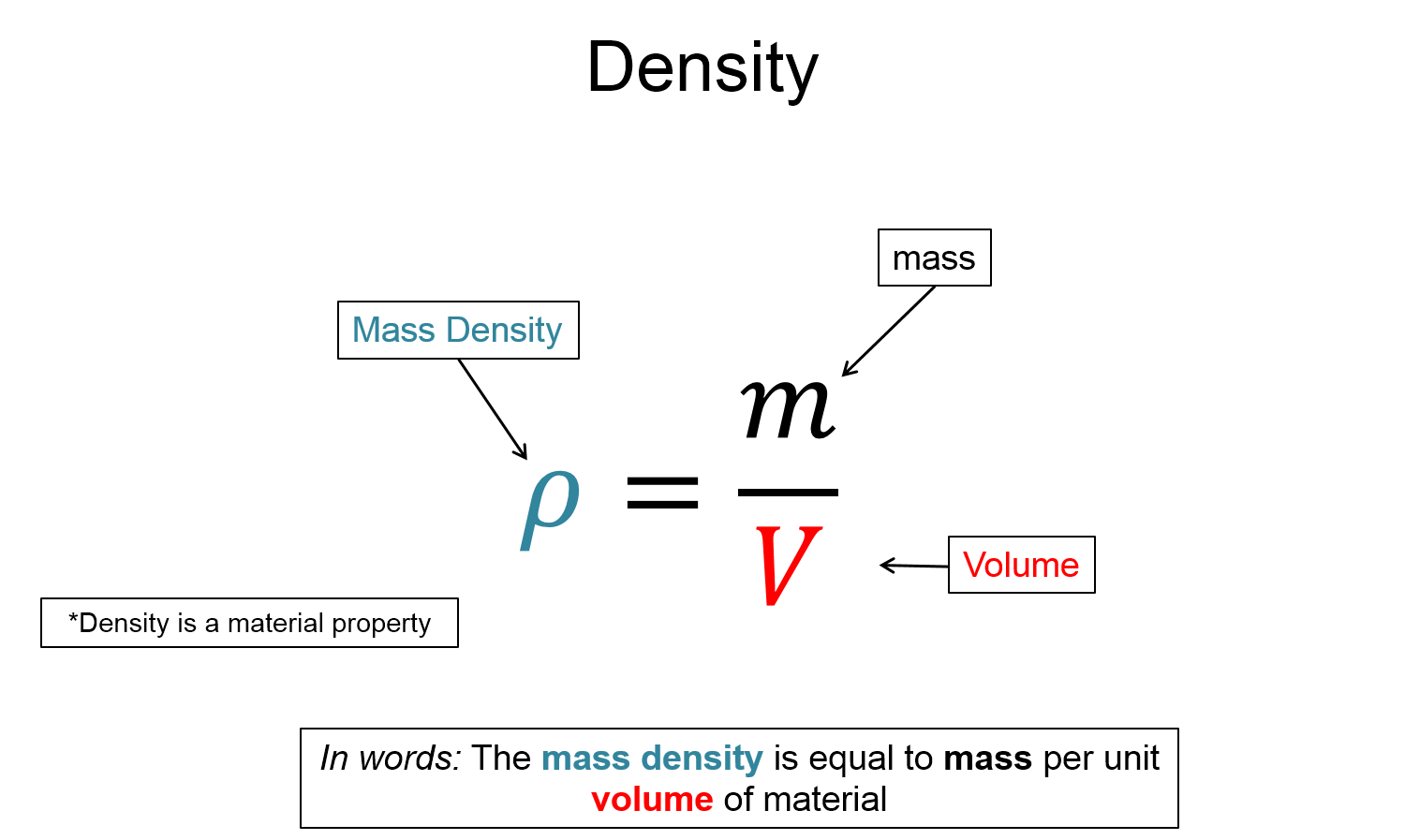
$P = \frac{F}{A}$
Pressure (P), Force (F), Area (A)

Graphical
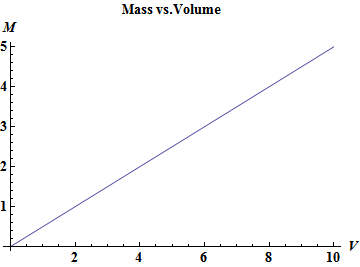
The following plots the mass vs the volume where the slope of the line is the density $\rho$.
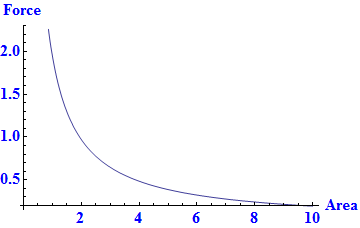
Pressure is force per area. The plot below describes pressure relative to force and area.
Descriptive
The density of a material is dependent on the ratio of the total mass of the material and the volume of the material.
Pressure is the total force (F) per area (A).
Experimental
The following video is a layering density experiment where various objects and liquids are poured in to a column to demonstrate varying densities.
If we submerge and empty water bottle into a bath of hot water the bottle will expand. This is due to the increased pressure inside of the bottle. The air molecules are excited due to the increased temperature of the internal temperature of the bottle thus increasing the kinetic energy of the air molecules which collide with the walls of the water bottle at a higher velocity, thus increasing the amount of force applied to the inner surface area of the bottle.