Angular momentum helps us think about how difficult it would be to stop something from spinning if the rotational speed of the object and it's distribution of mass around the axis of rotation was varied. Stopping a merry-go-round is much harder when its full of children. Angular momentum is often used when talking about extended masses, such wheels rotating about an axle or ice skaters spinning faster and faster. Specifically it tells you how hard it is to stop a rapidly spinning object in a certain amount of time, much like linear momentum tells you how hard it is to stop something moving translationally in a given amount of time. It is a useful property for understanding the orbits of satellites and planets. Like linear momentum, angular momentum is conserved for isolated systems. Physics assumes the angular momentum of the universe is a constant!
Here is a quick concept trailer of angular momentum from OpenStax
Pre-lecture Study Resources
Watch the pre-lecture videos and read through the OpenStax text before doing the pre-lecture homework or attending class.
BoxSand Introduction
Rotation and Conserved Quantities | Angular Momentum and Rotational Kinetic Energy
Angular Momentum
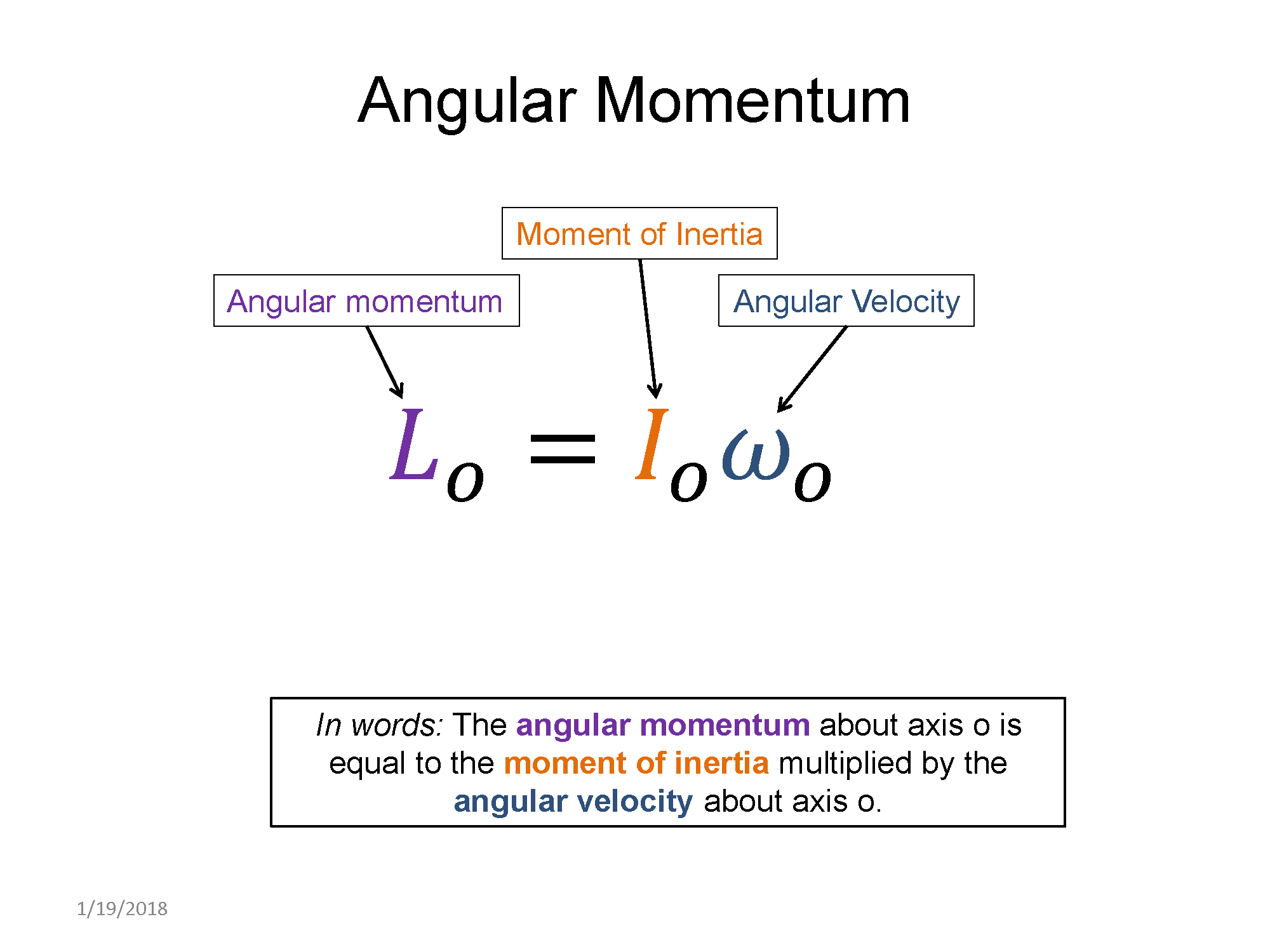
Just as linear momentum represents a quantity that scales a mass by its velocity, angular momentum represents a quantity that scales the extended mass of an object by its angular velocity. It is mathematically defined as
$ L = I \omega$
where $I$ is the moment of inertia of an object, and $\omega$ is its angular velocity. Angular velocity is a vector quantity but we will not be discussing that aspect and instead will use a sign convention that it can take positive or negative values: (+) for counter-clockwise motion or (-) for clockwise motion. Angular momentum is helpful for understanding the motion of real-life objects, such as rotations of galaxies about their galactic center or the motion of a merry-go-round as a child walks from the outside in.
If we compare the linear and angular momentum equations directly we see they are very similar:
$p = m v $
$L = I\omega$
Where the moment of inertia, which represents how the mass is distributed about some point, takes the place of mass; and omega, which represents how that extended mass is moving about a point, takes the place of velocity.
As a quick example, imagine a wheel with a mass of 1kg and a 50 cm-diameter spinning about an axle at a rate of 2 rad/sec. If we assume the spokes are massless we can use the moment of inertia for a spinning ring, $I_{ring} = mr^2$, to describe the wheel, where $r$ is the radius of the wheel and $m$ is the mass of the wheel:
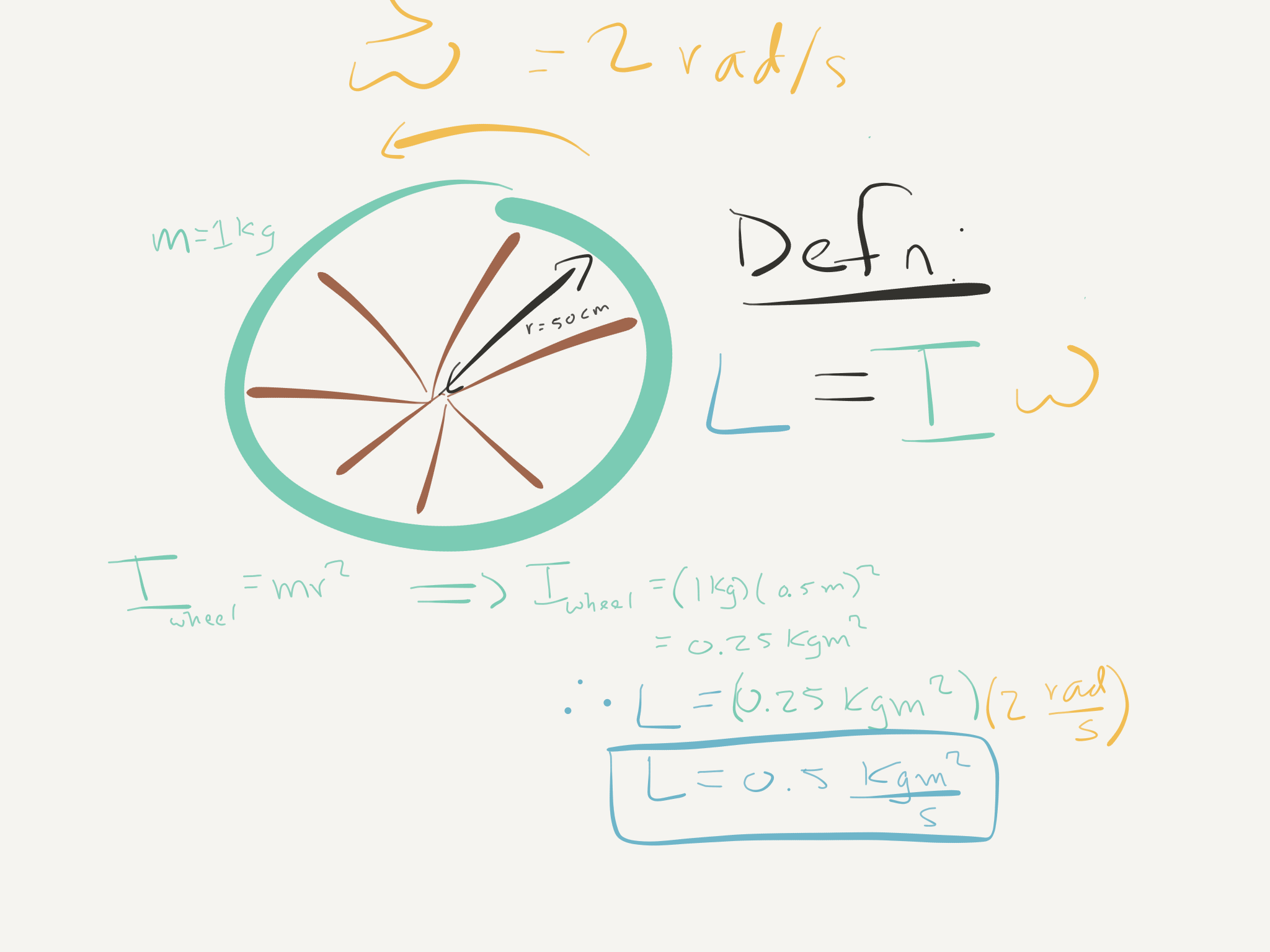
above is the sort of calculation you will do a lot of in this section.
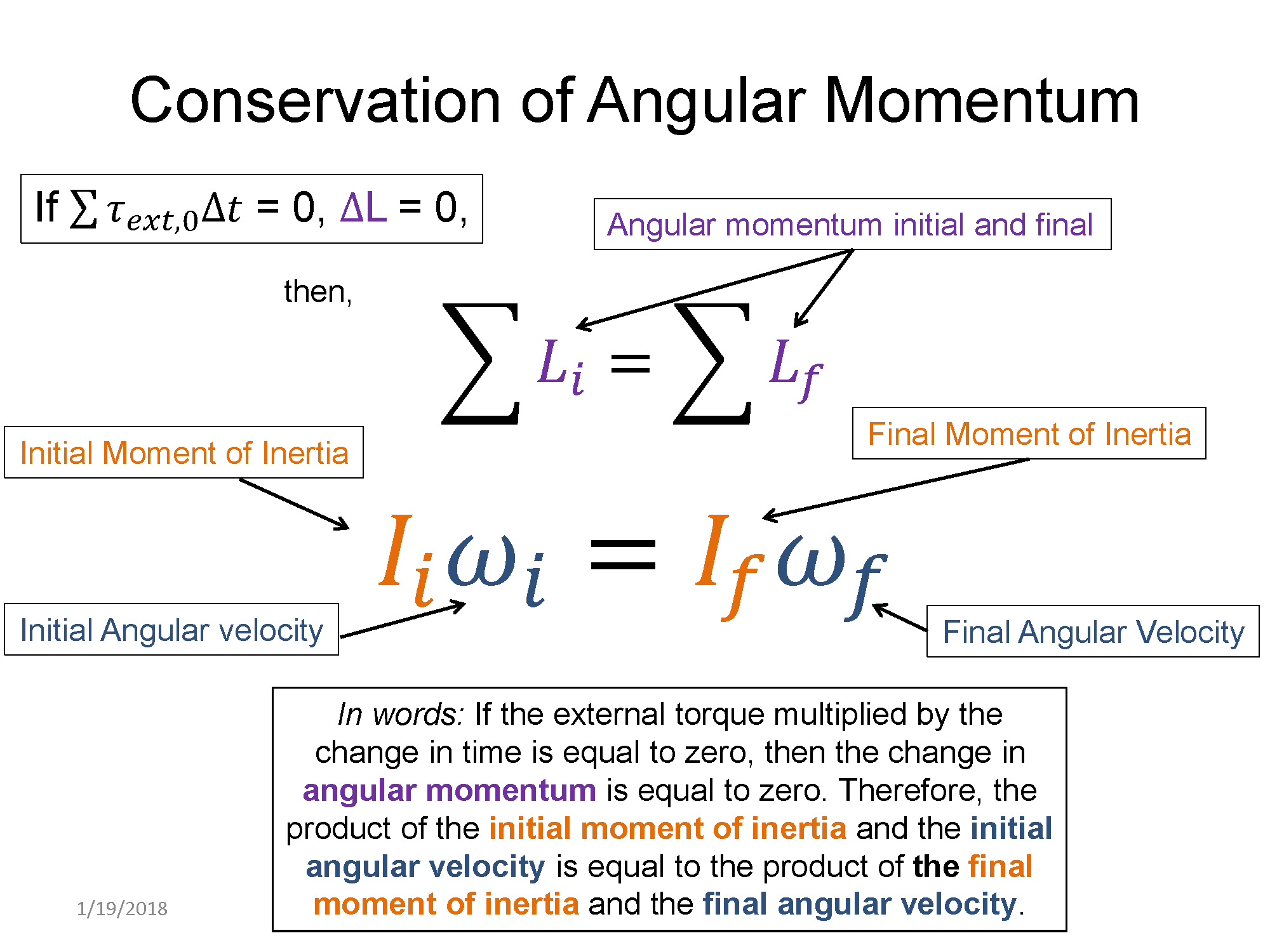
Just like linear momentum, angular momentum is a conserved quantity with its own conservation law:
$\Sigma \tau_{ext} \Delta t = \Delta L$
This equation says that if the net external torque is zero, angular momentum will not change. This equation is just like the impulse-momentum theorem from linear momentum and, when we plot $\Sigma \tau_{ext}$ (also known as $\tau_{net}$) versus $\Delta t$, we can find the area under the curve to determine how much angular momentum has changed in some time interval. This is exactly the same as how we used plots of $F_{external}$ versus $\Delta t$ to determine how much linear momentum would change in some time interval!
For example, imagine you're riding an electric scooter. The electric motor in the scooter applies a torque to the wheels to get them to spin. We can determine how much angular momentum is being added to the wheel by examining the torque versus time plot:
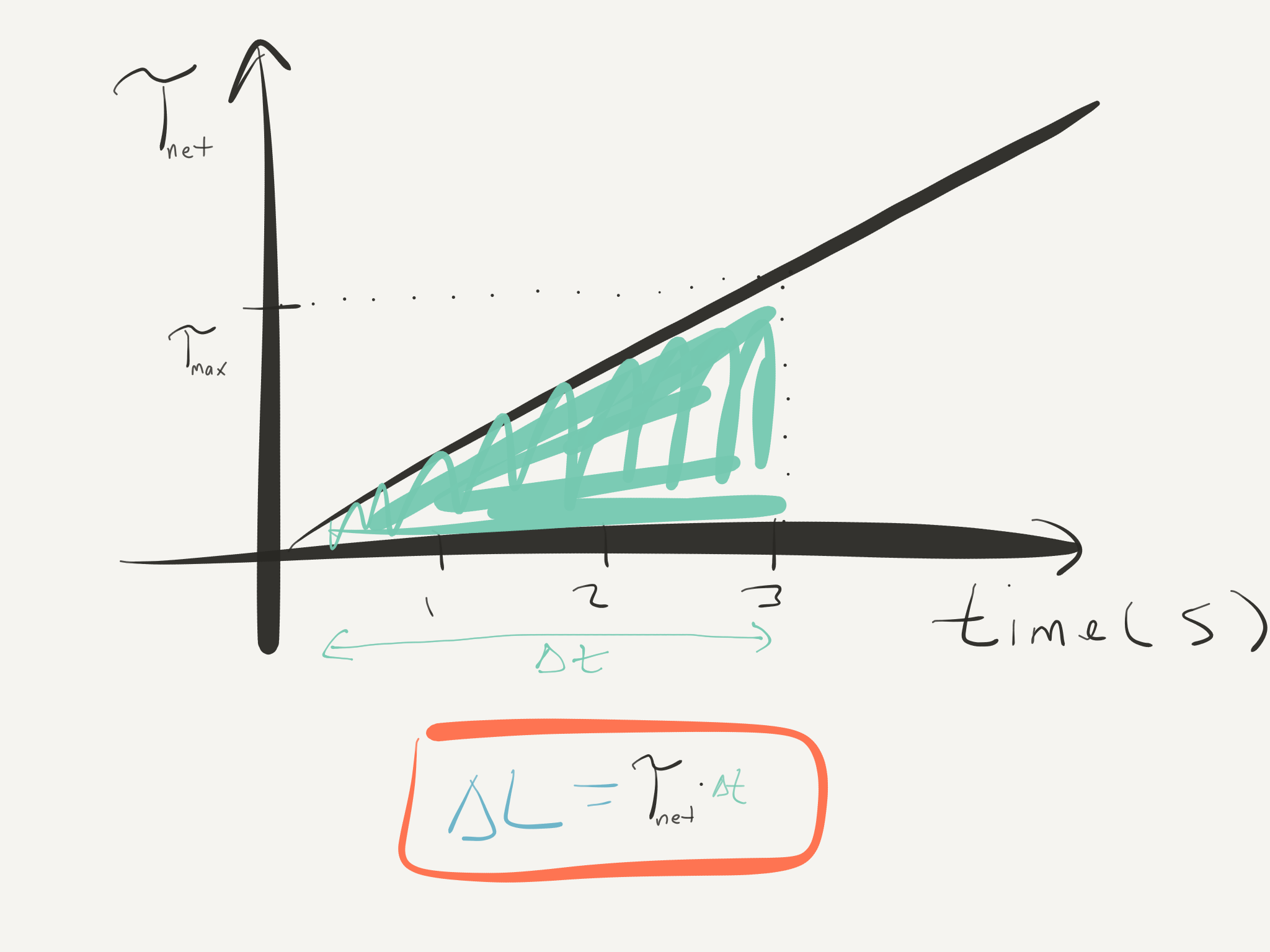
And since we know $\Delta L = \Delta (I\omega)$, and we know $I$ isn't changing (the diameter of the wheels on your scooter isn't changing) we can find the change in angular velocity:
$ I_{wheel} \Delta \omega = \Delta L$ and $\Delta L = \tau_{motor} \Delta t$
→$\Delta \omega_{wheel} = \frac{\tau_{motor} \Delta t}{I_{wheel}}$
In general, to find a value for "tau times delta t" in the numerator of the right-hand-side, you will make triangles and squares out of the area under the curve; often (as in this example) the "tau versus delta t" looks like $\frac{1}{2}bh$ where $b$ is the base length ($\Delta t$) and $h$ is the height ($\tau_{max}$), which reduces to $\frac{1}{2}{\tau_{max}}\Delta t$
Rotational Kinetic Energy
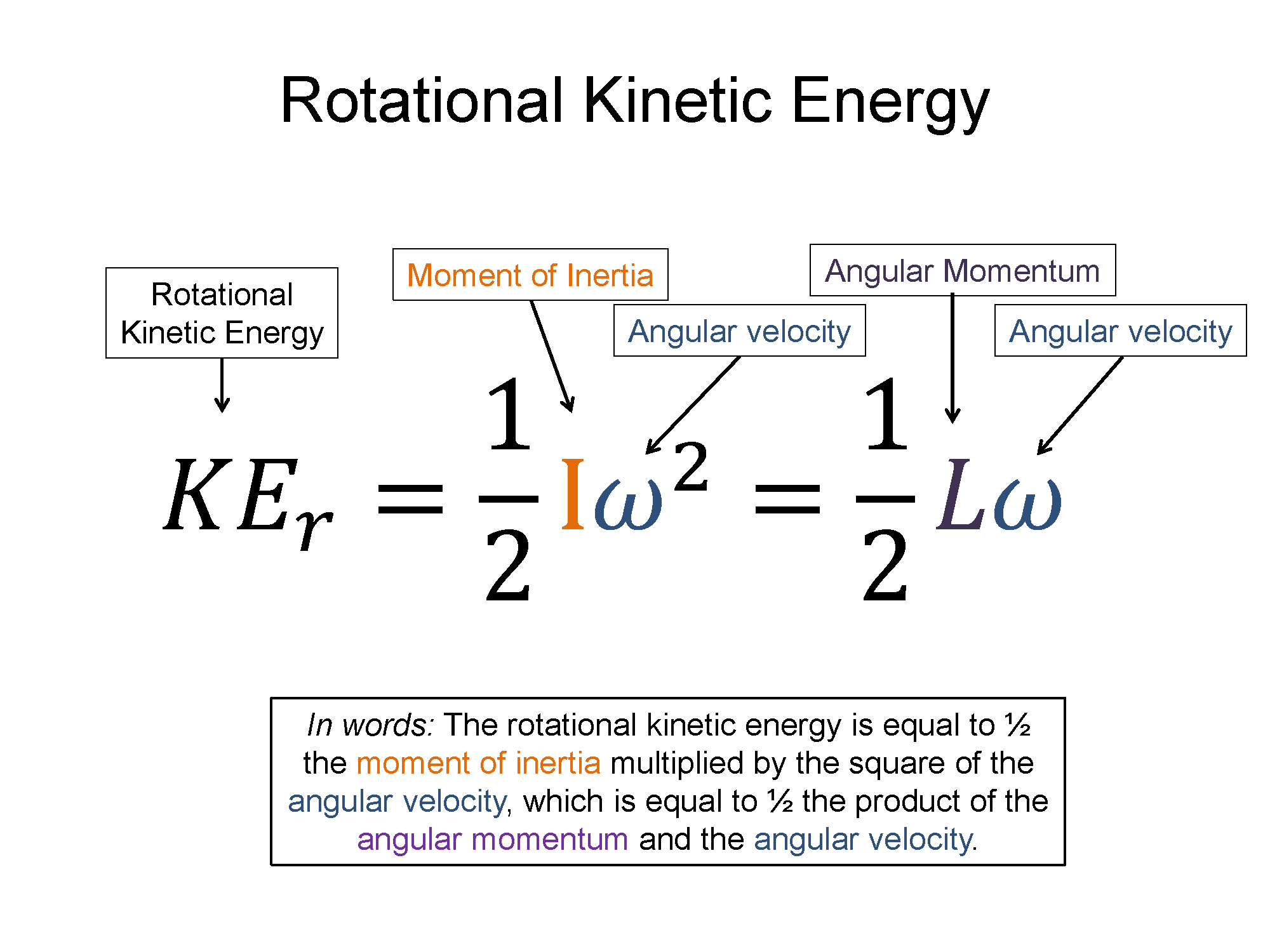
Rotational kinetic energy accounts for the collective motional energy of mass(es) rotating about an axis. Imagine a bowling ball sliding on a frictionless surface with some speed v. It would have linear kinetic energy ($\frac{1}{2}mv^2$) from the translational motion of all the particles making up the ball. If the ball was instead rolling, but yet it's center of mass still had a speed v, there would be additional motional energy in the rotation of all the particles that make up the ball about the axis of rotation. Rotational kinetic energy ($\frac{1}{2}I\omega^2$), where I represents the moment of inertia about the rotational axis and $\omega$ represents the angular velocity about the axis of rotation, accounts for this additional motional energy.
$K_{total}=K_{linear}+K_{rotational}$
$K_{total}=\frac{1}{2}mv^2+\frac{1}{2}I\omega^2$
After accounting for this new form of rotational kinetic energy, the rest of a standard energy analysis follows. Add up all the initial total mechanical energy (E), kinetic (K) plus potential (U), then add the work from non-conservative forces, and set that equal to the final mechanical energy.
$\sum E_i + W_{nc} = \sum E_f$, where $E = K_{linear} + K_{rotational} + U$
Key Equations and Infographics

Now, take a look at the pre-lecture reading and videos below.
BoxSand Videos
Required Videos
Suggested Supplemental Videos
OpenStax Reading
OpenStax Section 10.4 | Rotational Kinetic Energy: Work and Energy Revisited
OpenStax Section 10.5 | Angular Momentum and Its Conservation
OpenStax Section 10.6 | Collisions of Extended Bodies in Two Dimensions
OpenStax Section 10.7 | Gyroscopic Effects: Vector Aspects of Angular Momentum
Fundamental examples
1. Calculate the angular momentum for a satellite with mass $m=50kg$ that is orbiting a distance $r=1000 km$ with a linear velocity of $v= 100 m/s$ from its axis of rotation.
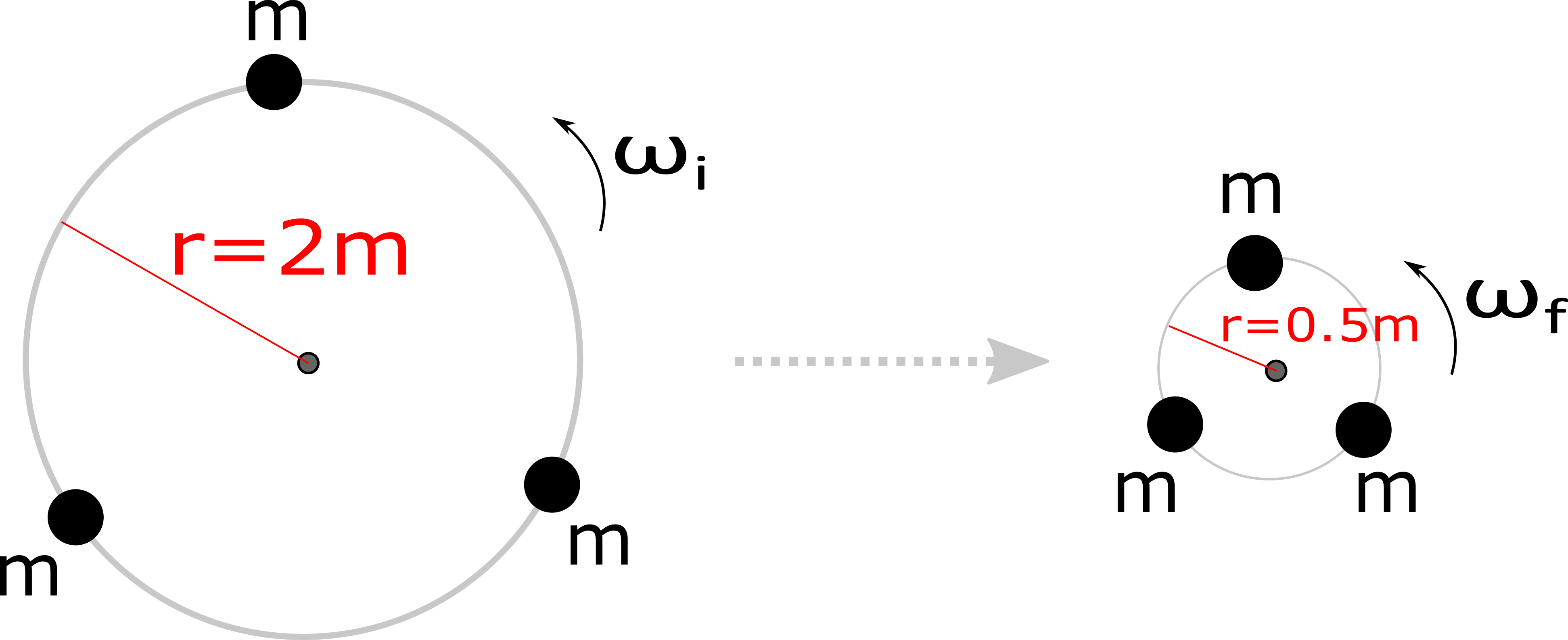
2. Three objects of equal mass, $m=5kg$, are located along a thin rod, of mass $m =1 kg$ bent into the shape of a circle of radius $2 \, meters$ shown in the left part of the figure below. Initially the system is rotating about the center of the circle with an angular velocity $\omega = 6.3 \, rad/s$. The masses are then carefully adjusted, such that no net external torque is applied to the system. The three masses now reside on a smaller circular rod of $m = 1 kg$ and radius $r = 0.5 \, m$ as shown in the right part of the figure below. What is the new angular velocity?
3. a) Sally and Betty go 'round the outside, 'round the outside, 'round the outside of a merry-go-round and push it clockwise (as seen from a birds-eye view) at a rate of $\omega= 3 \frac{rad}{s}$. Sally has $m_S = 50kg$ while Betty has $m_B = 60 kg$. The merry-go-round has mass $m_{m} = 500kg$ and a radius $r_m = 2 m$. They give it a final push and simultaneously jump on at opposite sides of the merry-go-round in a manner such that they exert no torque on it, and it remains spinning at $\omega=3 rad/s$. What is the angular momentum of the merry-go-round+Sally+Betty system?
b) A monkey with $m_M = 10 kg$ falls out of a nearby tree and lands on Betty's back. If the monkey attaches to Betty in such a way that it exerts no torque on the system, how many revolutions will the merry-go-round revolve through in 1 minute?
(A little beyond fundamental, but interesting nonetheless) c) Betty remembers her mother telling her that the best way to get a monkey off of your back is with the help of a good friend. She asks Sally to give her a hand. Sally agrees, and walks across the merry-go-round to help out Betty. Sketch a plot of the angular momentum of the system as Sally walks across the merry-go-round. Label the plot with the value of the angular momentum at the beginning, middle, and end of her walk. Then do the same for the angular velocity of the system (sketch this on the same plot). )
Short foundation building questions, often used as clicker questions, can be found in the clicker questions repository for this subject.
This resource has a nice set of simple example problems with instant feedback on your answer.
1. A solid sphere with a mass of $3 \, kg$, and radius of $0.2 \, m$ is rolling across a horizontal ground with a constant speed of $5 \, m/s$. If the sphere then encounters an inclined plane as shown in the figure below, to what height, $h$, will the sphere reach before coming to rest? The solid sphere has a moment of inertia of $I_{com} = \frac{2}{5} m \, r^2$

2. Volvo designed what they call the "Kinetic Energy Recovery System" (KERS); a mechanical system that uses the rotational kinetic energy of a rotating flywheel ( a flywheel is basically a solid disk) to help accelerate their car along a straight line. Let's assume we use Volvo's KERS to drive a go-kart of total mass $135 kg$. Our go-kart requires a constant power of $5,000$ watts to accelerate from rest to the maximum speed before all the rotational kinetic energy of the flywheel is transferred to the linear motion of the go-kart. Power is defined as $P = \frac{energy}{time}$, and a watt ($W$), is equal to $1 \frac{J}{s}$. If all the rotational kinetic energy of the flywheel is transferred to the linear motion of the go-cart after $6$ seconds, how fast will the go-kart be traveling?
CLICK HERE for solutions.
Short foundation building questions, often used as clicker questions, can be found in the clicker questions repository for this subject.
Post-Lecture Study Resources
Use the supplemental resources below to support your post-lecture study.
Practice Problems
Recommended example practice problems
- Openstax, Bottom of page there are 6 good problems, Website Link
-
3 multi-part problems involving Angular Momentum, PDF Link
-
10 problems, skip problem 2, PDF Link
For additional practice problems and worked examples on rotational momentum, visit the link below. If you've found example problems that you've used please help us out and submit them to the student contributed content section.
Additional Boxsand Study Resources
Additional BoxSand Study Resources
Learning Objectives
Summary
Angular Momentum
The objective is to analyze systems where angular impulse can be used to explain changes in angular velocity. For systems where the angular impulse is negligible, conservation of angular momentum can be used to understand changes in the motion of the system.
Rotational Energy
The objective is to expand our energy model to include rotational modes of kinetic energy, and to apply work and conservation of energy analyses to appropriate systems.
Atomistic Goals
Students will be able to...
Angular Momentum
- Define angular momentum about a reference axis for a distribution of mass as the moment of inertia multiplied by the angular velocity and show how it's analogous to the translation counterpart.
- Construction a mathematical representation for Newton's 2nd Law for Rotation, in terms of change in angular momentum vs. time.
- Compare and contrast the mathematical forms of angular momentum and Newton's 2nd Law for Rotation to their translational counterparts.
- Demonstrate that net torque applied over a time interval is an angular analog to translational impulse and analyze systems using this approach.
- Show that in the graphical representation the impulse is the area under a net torque vs. time curve.
- Show that for a system with zero (or near zero) impulse, the angular momentum of the system is conserved.
- Apply conservation of angular momentum to appropriate systems involving the mass distribution changing.
- Apply conservation of angular momentum to appropriate systems involving collisions.
- Explain the vector nature of angular momentum in a conceptual way and how a non-zero net torque can change the direction but not necessarily the magnitude of the angular momentum.
- Differentiate when an angular momentum analysis is more appropriate than linear momentum.
Rotational Energy
- Define rotational kinetic energy and identify the form-like similarity to that of translational kinetic energy.
- Identify when there is rotational and/or translational energy, including rotational modes of spin and rolling.
- Extend the work-energy theorem to include rotational work and identify the form-like similarity to translational work.
- Apply rotational work as the area under a torque vs angular displacement curve.
- Expand the conservation of energy framework to include rotational kinetic energy and external rotational work.
- Apply, using the mathematical representation, rotational kinetic energy in an energy analysis.
- Apply, using the physical and/or descriptive representations, rotational kinetic energy in an energy analysis.
- Differentiate between mass distributions and how they affect the partitioning between translational and rotational energy.
- Differentiate when angular momentum and rotational energy are appropriate analyses and that one may be conserved while the other is not.
- Define the rotational energy in terms of the angular momentum and analyze a system using this form.
YouTube Videos
Doc Schuster's video tutorial on angular momentum
Bozeman physics help us understand angular momentum through a simple approach
Khan Academy's approach to angular momentum
Khan Academy presents rotational kinetic energy.
Doc Schuster discusses Kinetic Energy of Rotation
This video and it's part two counterpart, provide a good introduction to rotational kinetic energy.
Part two
Simulations
For additional rotational momentum simulations on this subject, visit the simulations repository.
This is a simulation of racing different rolling objects down a ramp. Since each object has a different moment of inertia but the same mass and radius, you can see how different objects store more/less energy in the rotational kinetic energy.
- This Java Applet will require you to add the site URL to your Java Exceptions list
- Be sure to turn on friction because without it, nothing rolls.
For additional simulations on this rotational energy simulations, visit the simulations repository.
Demos
Conservation of angular momentum of a sphere changing radius
This is a really great overview coupeld with many demonstrations.
If an object is rotating about an axis it possesses rotational kinetic energy. This energy term must be added to the mechanical energy of the system. Consider a spinning disk. If the center of mass of the disk wasn't moving, it has no translational (linear) kinetic energy. But it does have some motional energy that we call rotational kinetic energy. The equation for rotational kinetic energy is below, where;I is the moment of inertia about the axis of rotation and $\omega$ is the angular velocity of the object.
$KE_{rotational}=\frac{1}{2}I\omega^2$
For additional demos involving this subject, visit the demo repository
History
Oh no, we haven't been able to write up a history overview for this topic. If you'd like to contribute, contact the director of BoxSand, KC Walsh (walshke@oregonstate.edu).
Physics Fun
This is a cool video that relates angular momentum to ballet.
This is the coolest YouTube video. It's hilarious and riveting.
Check out the anti-gravity wheel!
This gif shows how cats always land on their feet - how they can rotate in mid air and not change their total angular momentum vector.

Ever tried the water bottle flip challenge? Check out the video below to see how it's possible.
Other Resources
Hyperphysics introduces the concept of angular momentum
The people at physicslab have a simple introduction to angular momentum with a brief talk about the right hand rule
This is a long lecture slide that discusses all areas of rotational dynamics and angular momentum
This link is to HyperPhysics which gives a very brief overview of the topic of rotational kinetic energy.
A Textbook overview of Kinetic Energy.
Resource Repository
This link will take you to the repository of other content on this topic.
Problem Solving Guide
Use the Tips and Tricks below to support your post-lecture study.
Assumptions
Like it sounds, angular momentum is the rotational equivalent of linear momentum and functions in most of the same ways. Angular momentum is quantity that can show how much energy or force a rotating object can transfer into another object, but has with it some unique and useful properties! (see below).
- Angular momentum is another fundamental quantity in physics that is always conserved, but for our types of analysis, it can be hard to quantify how it is conserved unless there are no external torques on the system. Under this assumption, angular momentum cannot transfer outside our system in a complicated way (e.g. have the energy associated with it turned into force, linear momentum, or some other type of energy). This will usually be the case, so before using conservation of angular momentum, ensure there are no net torques on the system.
- Like the moment of inertia, angular momentum is built out of linear (to the first power) quantities and that means if we have multiple objects, each with angular momentum, in our system, we can freely and easily add those individual angular momentums together to get a total angular momentum for the system!
- Angular momentum is useful for describing dynamic systems where we care about how they move through space, because angular momentum is a vector and contains directional information! It turns out our other methods of analysis are pretty inadequate for these types of situations: Torque analyses is hard to quantify as it transfer through different objects through time (you have to use impulse, but we won't in this class because momentum is more widely used), rotational kinematics only works under the special condition that $\alpha=constant$ (we can analyze a LOT more types of systems with angular momentum!) and rotational energy analysis can't tell us anything about directional components, because unlike angular momentum, energy is a scaler quantity not a vector!
Checklist
Angular Momentum
Draw a pictorial representation of the initial and final states of the system. Identify the axis of rotation of your system and sketch vector(s) connecting the rotating mass(es) to the axis of rotation. For example, for a wheel spinning on an axle that is increasing in angular speed, a physical representation may look like:
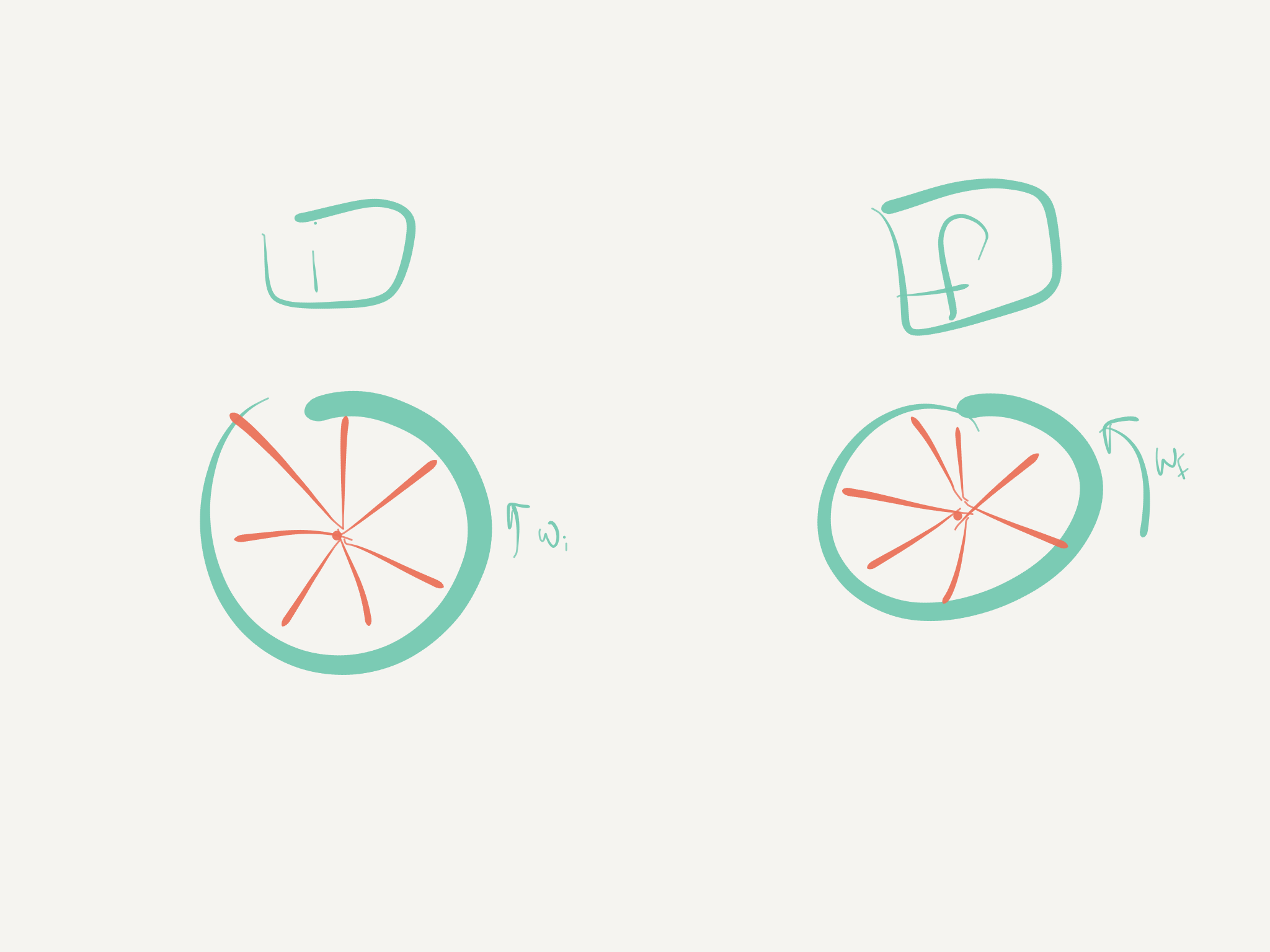
If you have more information, such as the moment of inertia or angular acceleration, include it on this diagram.
Always calculate (or look up) the moment of inertia of your system first, or the moments of inertia of the objects in your system. If it is a multi-stage problem and you have enough information, calculate the moments of inertia in each stage before doing any other part of the problem.
Angular momentum problems fall under a two general categories:
i) Problems involving no external forces (and therefore no torque):
1. If you have enough information, calculate the initial angular momentum $L_i$ of the system. Since there are no external forces acting on the system ($\tau_{net} = 0$), angular momentum is conserved and thus the initial angular momentum $L_i$ is equal to the final angular momentum $L_f$.
2. Since $\Sigma L_i = \Sigma L_f $, there are only two quantities related to angular momentum that might change: moment of inertia $I$ or rotational velocity $\omega$. This suggests that $I$ will change if, for example, a person who is spinning in an office chair pulls in their arms and legs, changing the position of mass in the system relative to the axis of rotation. Since $L=I \omega$ and $L$ is constant, $\omega$ must change proportionally. Many problems in the $\tau_{net} = 0$ category center around calculating $\omega$ for a changing $I$ or vice-versa. Use proportional reasoning to determine these changes.
For problems where the moment arm or moment of inertia changes (a satellite drops to a lower orbit or a figure skater pulls their arms in), calculate the new moment of inertia if you have enough information.
ii) Problems involving external forces that are causing a net torque $\tau_{net}$.
1. If you have enough information, sketch a torque versus time plot. The area under this plot is the amount of torque applied to the system in a given time interval - and thus the total change in angular momentum.
2. In general, if torque is applied for some amount of time, it will change either $I$ or $\omega$. The problem statement should include enough information for you to determine which is changing, so refer to that, do some algebra, then plug and chug.
* Angular momentum problems connect very naturally to rotational kinematics problems, just like linear momentum problems often connect to linear kinematics problems. Often when you have gone through the algorithm above, you are now left with a new $\omega$ value, which you will apply to the next stage of a rotational kinematics problem.
Rotational Energy
1. Identify the system of interest.
2. Determine what forms of energy are present: linear and/or rotational kinetic energy, spring and/or gravitational potential energy.
3. Identify any non-conservative work being done on the system.
4. Apply conservation of energy to the initial and final states of the system.
$E_i + \Sigma W_{non-conservative} = E_f$
$K_{linear_i} + K_{rotational_i} + U_i^g+U_i^s + \Sigma W_{non-conservative} = K_{linear_f} + K_{rotational_f} + U_f^g+U_f^s$
Misconceptions & Mistakes
- A change in angular momentum can be a change in $I$ or a change in $\omega$ (or both).
- Like linear momentum, angular momentum is a vector but not a force, so it should not show up on a FBD.
- Conservation of angular momentum does not mean that the angular momentum of each object within the system is conserved individually; It means that the system as a whole conserves angular momentum.
- An object's kinetic energy can be split into two parts; its translation kinetic energy of the center of mass, and its rotational kinetic energy about the center of mass. A common mistake is to "double count" the kinetic energy of an object. For example if a box is going around a frictionless vertical loop-de-loop, the correct energy of the box+earth system is the translation kinetic energy of the center of mass of the box, the change in gravitational potential energy as the box goes up or down the loop-de-loop, and the rotational kinetic energy of the box about the center of mass of the box. The common mistake in this scenario is to also include a rotational kinetic energy of the center of mass of the box about the center of the loop-de-loop; this is incorrect since we already have the translational kinetic energy of the box accounted for, thus it is sort of like "double counting". Note: many problems like this example ignore the rotational kinetic energy of the box about its own center of mass while going around the loop-de-loop because it is typically much much smaller than the translational kinetic energy and gravitational potential energy.
- Up until this point, we have typically assumed pulleys were "massless", thus it is easy to overlook the mass of the pulley in problems. Basically, read the problem carefully; if a pulley has mass, do not forget to include its rotational kinetic energy.
Pro Tips
- Make sure to account for the vector nature of $L$ by assigning it a (+) or (-) sign.
- Recall that the moment of inertia of a system depends on the axis of rotation and the distribution of mass around that axis. For a point particle, the moment of inertia about an axis "$o$" is $I_o = m \, r^2$, where $r$ is the distance the point particle is from the axis of rotation. If your system includes more than one point particle, the moment of inertia for the system is the addition of each individual object's moment of inertia about the axis "o". For example, a system with two point particles at different distances from an axis or rotation has a moment of inertia of $I_o = m_1 \, r^2_1 + m_2 \, r^2_2$. We can generalize this addition feature of moment of inertia for systems that include more than one type of geometric object. For example, if your system consists of a ring of mass $M$ rotating about the center of the ring, and a point particle of mass $m$ located on the ring, the moment of inertia of this system is also just the sum of each individual object's moment of inertia, $I_o = \frac{1}{2} M r^2 + m \, r^2$.
- Draw a physical representation when faced with an angular momentum problem. This includes labeling initial and final angular velocities, forces, system boundaries, rotation axis, moment arms. There are a lot of quantities involved and sign conventions to keep track of, thus getting a physical representation drawn will help organize your thoughts on how to proceed with solving the problem. Drawing your physical representation to a relative scale will also help you visualize the systems motion and allows you to double check your final answers with your representation.
- If a problem is asking about orbits,define the central force holding objects in orbit as part of the system. For example, the Earth is held in orbit around the sun by a central force (gravity), and a marble on a string is being held in its orbit by tension.
- When presented with a problem, draw a physical representation including information about velocities, changes in height, geometric quantities such as the radius of a rotating sphere, forces, and a system boundary. The physical representation will be useful in organizing your thoughts and will help determine which forces are acting on your system.
- If you decide to use conservation of energy to approach a problem, start with the definition of conservation of energy $\sum{E_i} + W_{nc} = \sum{E_f}$. Then consult your physical representation to mentally go through the list of the different forms of energy, (e.g. translational kinetic energy, rotational kinetic energy, gravitational potential energy, etc..) and decide if your system has that form of energy. If so, include all forms of energy in the conservation of energy equation. Starting from the definition will help ensure that you do not miss any forms of energy included within your system.
Multiple Representations
Multiple Representations is the concept that a physical phenomena can be expressed in different ways.
Physical
As we did previously with conservation of momentum, we show before and after snapshots. Consider this ice skater spinning on her skate with her arms out,

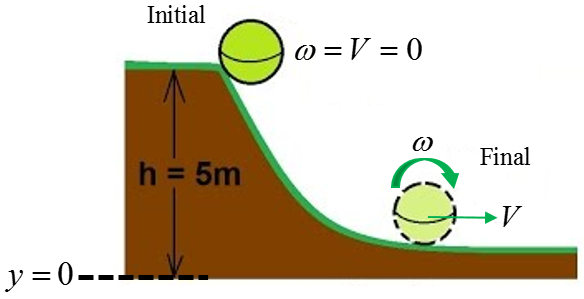
As the ball rolls down the hill the gravitational potential is transferred to both transverse and translational kinetic energy.
Mathematical
$L = I\omega$
if $\sum \tau \Delta t = 0$ then $\sum L_i = \sum L_f$
The change of angular momentum is equal to the net torque on the system multiplied by the amount of time.
$\Delta L = \Sigma \tau \Delta t$
Angular momentum ($L$), Angular frequency ($\omega$), Moment of inertia ($I$)



The energy of a rolling object,
$\sum E_i + W_n = \sum E_f$
$E = K_{lin}+K_{rot}+U^g+U^s$
$K_{rot} = \frac{1}{2}I \omega^2$

Graphical
The first graph depicts the change in angular momentum L as the area under the net torque curve. In addition, the last graph depicts a situation where some is moving on a merry-go-round. Where the merry-go-round angular frequency is in blue and the person is in red. When the person starts to walk in the same direction as the merry-go-round is spinning, the persons angular frequency increases relative to the merry-go-round. However, the merry-go-round's angular frequency decreases as a consequence of conservation of angular momentum.
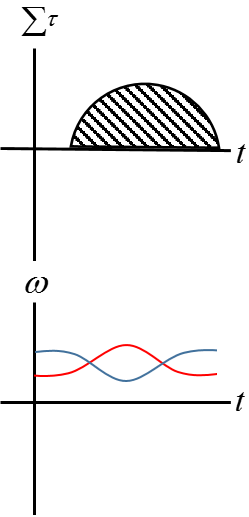
The area under the net torque vs. angle graph is equal to the rotational work done.

Descriptive
An ice skater is spinning on the tip of her skates with her arms extended. Her angular momentum is conserved because the net torque on her body is negligibly small. The skater pulls her arms in changing her moment of inertia to $I'$. As angular momentum $L$ is conserved, the skater's angular velocity must increase if $I' \lt I$
Rotational kinetic energy is similar to normal kinetic energy of objects without rotation. For a wheel rolling down a hill, some of the gravitational potential energy is split between the transverse and translational motion. The physical representation above is a clear of example of this description.
Experimental
A classic angular momentum experiment uses a spinning stool and various weights. Watch the video the learn how this experiment works.
Drop a ball from some height h, and observe the ball only exhibit transverse motion. Now roll the ball down an incline, and observer the ball exhibit both transverse and translational motion.