Standing Waves occur when two waves with the same wavelength, are traveling in opposite directions. If the system that contains the waves is of a certain size, a resonance occurs and the standing waves become more pronounced.
Here is another OpenStax physics trailer to help motivate the subject of standing wave resonance and its application to our daily lives.
Pre-lecture Study Resources
Watch the pre-lecture videos and read through the OpenStax text before doing the pre-lecture homework or attending class.
BoxSand Introduction
Superposition of Waves | Standing Wave Resonance
When two waves with the same frequency and wavelength are traveling in opposite directions, they interfere in such a way that a characteristic Standing Wave Pattern shows up.
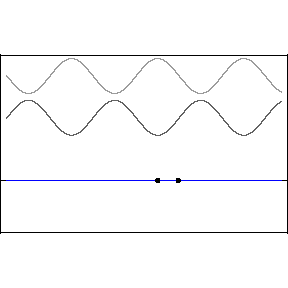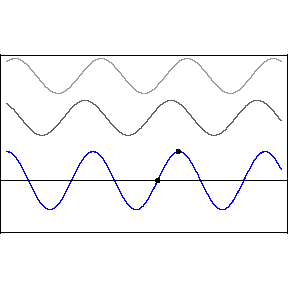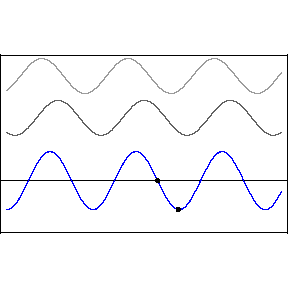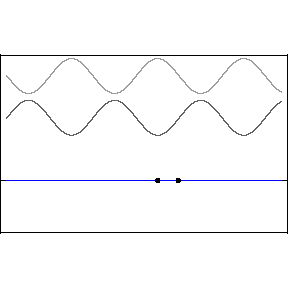
In the above animation the two top waves are added together through the principle of superposition (just added) and the resultant is the bottom wave. Notice in the resulting standing wave that there locations that are never displaced, these are the nodes of the standing wave. In between the nodes are locations that undergo large displacements, in fact much larger than when there was a single wave. These are called anti-nodes. The wave itself does not appear to be traveling, hence the term standing.
If the waves fit perfectly into the system that contains them, they can create a resonance. To determine what wavelengths match this system size condition you need to consider the Boundary Conditions (BC). Consider a wave sent down a taught string that reflects off the fixed end. Such a system is great for generating standing waves because the reflections at the end points ensure there are waves traveling in opposite directions, a requirement for standing waves. If the endpoints are fixed, the displacement must be zero there. So, conceptually, the longest wavelength that would fit in that system, is if the wavelength is twice the length of the string.
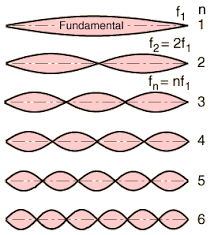
The fundamental mode shown above is the one with the longest wavelength. We represent the standing wave in this form with two lines weaving back and forth, but it's important to realize this is just a static represnetation of the actual wave pattern, which is animated below for the 4th harmonic. The fundamental mode is the first harmonic, folled by the next longest wavelength that match the boundary counditions, which would be the second harmonic.

If the length of the system is a value $L$, than the wavelengths that match the boundary conditions are equal to $\frac{2L}{m}$, where $m$ is any integer $m=1, 2, 3, ...$. These are the equations for systems where the ends are both fixed, or both free, so long as they are Symmetric boundary conditions.
If the ends are the opposite of each other the system is considered to be Anti-symmetric. There is then different series that determines the resonant modes. A summary of the two types of boundary conditions is below where $v$ is the speed of the wave in the medium and $L$ is the length of the system.
Symmetric Boundary Conditions:
wavelength $\lambda_m = \frac{2L}{m}$, frequency $f_m=m \frac{v}{2L}=mf_1$, where m=1,2,3,...
$\Delta f=f_{m+1}-f_m=f_1$
Antisymmetric Boundary Conditions:
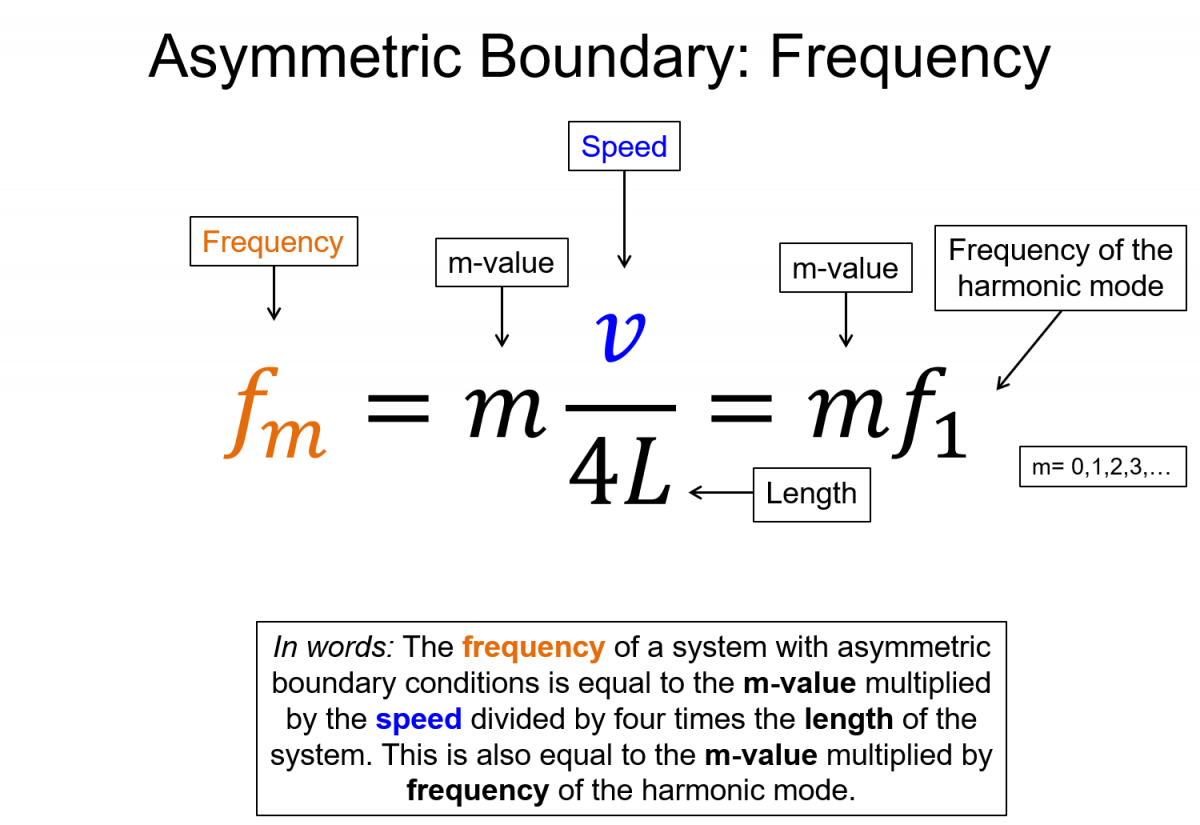
wavelength $\lambda_m = \frac{4L}{m}$, frequency $f_m=m \frac{v}{4L}=mf_1$, where m=1,3,5,...
$\Delta f=f_{m+2}-f_m=2f_1$
Some important features of these solutions are that for the symmetric BC, the difference in the frequency between adjacent modes is the fundamental frequency. For the anti-symmetric BC the difference is twice the fundamental. Also notice that in the anti-symmetric case you only use odd integers, which means the harmonic mode is not the same as the m-value. For example the 2nd resonance mode has an m-value of 3. In the symmetric case the harmonic and the m-value are the same.
Key Equations and Infographics
Now, take a look at the pre-lecture reading and videos below.
BoxSand Videos
Required Videos
Superposition - Constructive and Destructive Interference(5min)
Superposition - Standing waves(15min)
Superposition - Boundarys, Standing wave resonance(5min)
Superposition - Standing waves strings, fixed-fixed B.C.(14min)
Superposition - Standing waves strings, antisymmetric B.C.(9min)
Suggested Supplemental Videos
OpenStax Reading
Fundamental examples
1. A $1.5 \, m$ long string that is pinned down to a wall at both ends vibrates with a standing wave pattern that has $3$ antinodes.
(a) Which harmonic is this?
(b) What is the wavelength of this wave?
2. A soda bottle of length $26 \, cm$ can be modeled as an open-closed tube. While blowing air across the opening of the bottle, it is determined that the standing wave pattern inside has $3 \, antinodes.
(a) Which harmonic is this?
(b) What is the wavelength of this wave?
3. Human ear canal’s are roughly $2.4 \, cm$ long and can be modeled as an open-closed tube.
(a) What is the fundamental frequency and wavelength of an ear canal?
(b) What is the frequency and wavelength of an ear canal’s $2^{nd}$ harmonic?
4. An open-open tube of air supports standing waves at frequencies of $816 \, Hz$ and $1224 \, Hz$, and at no frequencies between these two. Which of the following are also resonant frequencies of the same tube?
(a) $204 \, Hz$
(b) $408 \, Hz$
(c) $612 \, Hz$
(d) $1428 \, Hz$
(e) $1632 \, Hz$
Click HERE for solutions.
Short foundation building questions, often used as clicker questions, can be found in the clicker questions repository for this subject.
Post-Lecture Study Resources
Use the supplemental resources below to support your post-lecture study.
Practice Problems
Conceptual problems
BoxSand's multiple select problems
BoxSand's quantitative problems
Recommended example practice problems
- Openstax has a few practice problems for standing wave resonance, Link
For additional practice problems and worked examples, visit the link below. If you've found example problems that you've used please help us out and submit them to the student contributed content section.
Additional Boxsand Study Resources
Additional BoxSand Study Resources
Learning Objectives
Summary
Summary
Atomistic Goals
Students will be able to...
YouTube Videos
This video shows Doc Schuster discussing standing waves in strings and tubes.
Other Resources
This link will take you to the repository of other content related resources .
Simulations
This animation shows how a pair of traveling waves on a string can create a standing wave. play with the button at the bottom to see how different standing wave patterns can be formed.
For additional simulations on this subject, visit the simulations repository.
Demos
Standing wave resonance, beat frequency, and a rad example of superposition of waves.
Standing waves in water and bonus rogue wave.
For additional demos involving this subject, visit the demo repository
History
Oh no, we haven't been able to write up a history overview for this topic. If you'd like to contribute, contact the director of BoxSand, KC Walsh (walshke@oregonstate.edu).
Physics Fun
Acoustic resonant modes of a levitating water droplet.
Standing waves inside a barrel create a train horn.
All you need to measure the speed of light is some Peeps, a microwave oven, and a little physics ingenuity.
Play the 2v4, why not what have you.
How to break a wine glass with a megaphone.
Other Resources
This PDF covers standings waves, in a fairly compact manner,
Hyperphysics standing wave resonance
Boston University covering standing wave resonance through analysing stringged instruments,
IsaacPhysics section on standing waves,
Other Resources
This link will take you to the repository of other content related resources .
Resource Repository
This link will take you to the repository of other content related resources.
Problem Solving Guide
Use the Tips and Tricks below to support your post-lecture study.
Assumptions
Resonances are natural physical phenomena, and exist in virtually everything. In this exploration, we will limit our study to symmetric and anti-symmetric conditions to make the math easier.
Basically, these resonances are how we can predict where the waves bouncing around our system will sync up to create constructive interference using just the geometry of our system, and so we can oftentimes reduce the wave analysis to simply the wavelength and then compare that wavelength to the geometry of the system to determine where and how many resonances exist in a particular system.
Checklist
These problems are mostly a series of choices and then using the equations given based on those choices. Let's cover them below:
Is the physical situation:
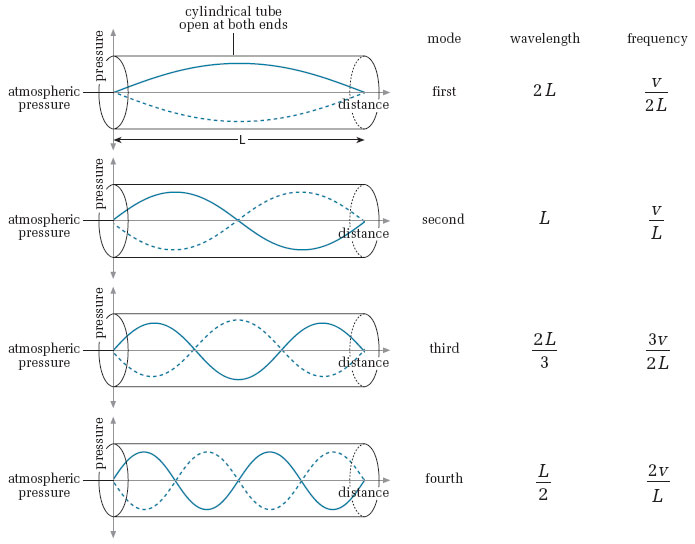
Open-open/closed-closed? and Therefore symmetric? Then use: $\lambda_m = \frac{2L}{m}, m = 1,2,3,4,5,...$
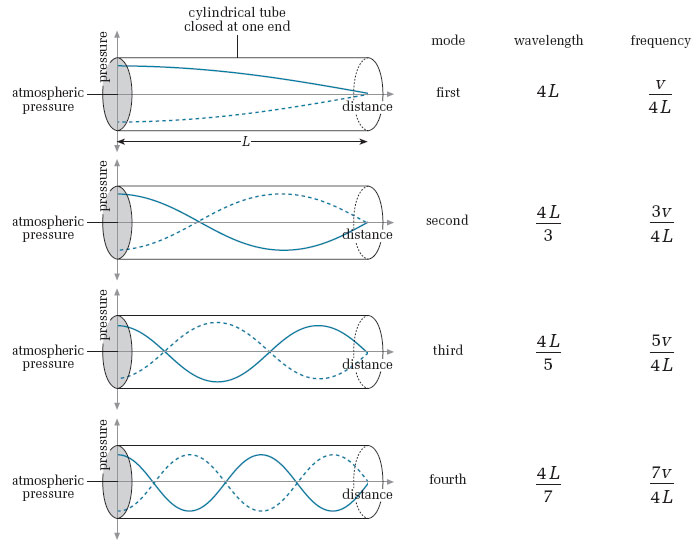
Open-closed/closed-open? And therefore anti-symmetric? Then use: $\lambda_m = \frac{4L}{m}, m = 1,3,5,7,9,...$
Visualizing what these geometric conditions mean is difficult without pictures, take a look at the graphical representations in the multiple representations below!
Misconceptions & Mistakes
- Graphs of pressure or position in a sound tube portray longitudinal oscillations, not transverse oscillations like in a string.
- The speed of sound is not what you use for the speed of a wave on a string. The wavespeed through a string is dictated by physical parameters of the string - its mass density and tension.
Pro Tips
- It's all about the boundary conditions. Make sure you understand how symmetric versus anti-symmetric boundary conditions change the resonant modes in a system. This is another section where there are very few variables to be manipulated in the "main equation" - mostly $L$, $v$, $m$, and $f$ or $\lambda$ - so there will be many qualitative questions about the nature of resonant modes. Spend some time reading the textbook section about creating standing waves on a string - this will help you develop intuition about how the physics of a node creates the mathematical boundary conditions.
- Common questions in this section involve identifying which resonant mode is active in a sytem given a snapshot of the system. Find a mnemonic device to help you identify resonant modes and become comfortable sketching out resonant modes on a string.
- Pay close attention to the medium in which your wave is propogating. The wavespeed $v$ is only equal to $343 \frac{m}{s}$ for sound waves traveling through air. All other media have different wavespeeds. Be extra careful about strings - their wavespeed is not something you can look up in a table, it is dictated by physical properties of the string and will change in every scenario.
- protip4life: if you ever have squeeky chalk, break it in half! That awful chalk + chalkboard squeel is due to a resonance phenomenon in the chalk: as you drag the chalk across the board, it drives a resonant oscillation down the length of the chalk. And, as we have studied in this section, if you change the size of a resonator, the resonant modes change. And luckily enough, it just so happens that short pieces of chalk are not the correct length to contain the resonant mode that makes that awful noise!
Multiple Representations
Multiple Representations is the concept that a physical phenomena can be expressed in different ways.
Physical
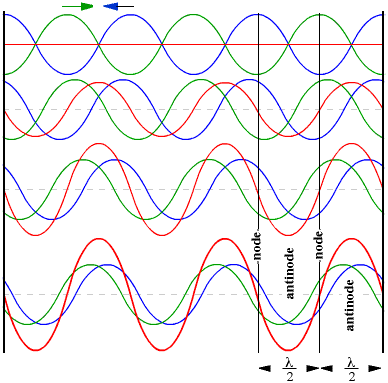
When two waves with equal frequency and magnitude travel in opposite directions they create standing waves. Below is a figure with several snapshots with a green wave traveling left and a blue wave traveling to the right, where the red line is the sum of the two traveling waves. As the waves propogate they add in a such a way to produce a standing wave.
Mathematical
Symetric boundary conditions,
$\lambda_m = \frac{2L}{m}, m = 1,2,3,4,5,...$
Antisymetric boundary conditions,
$\lambda_m = \frac{4L}{m}, m = 1,3,5,7,9,...$
$f_{m} = \frac{\nu}{\lambda_{m}}$
Wavelength ($\lambda$), Velocity ($\nu$), Integer ($m$)


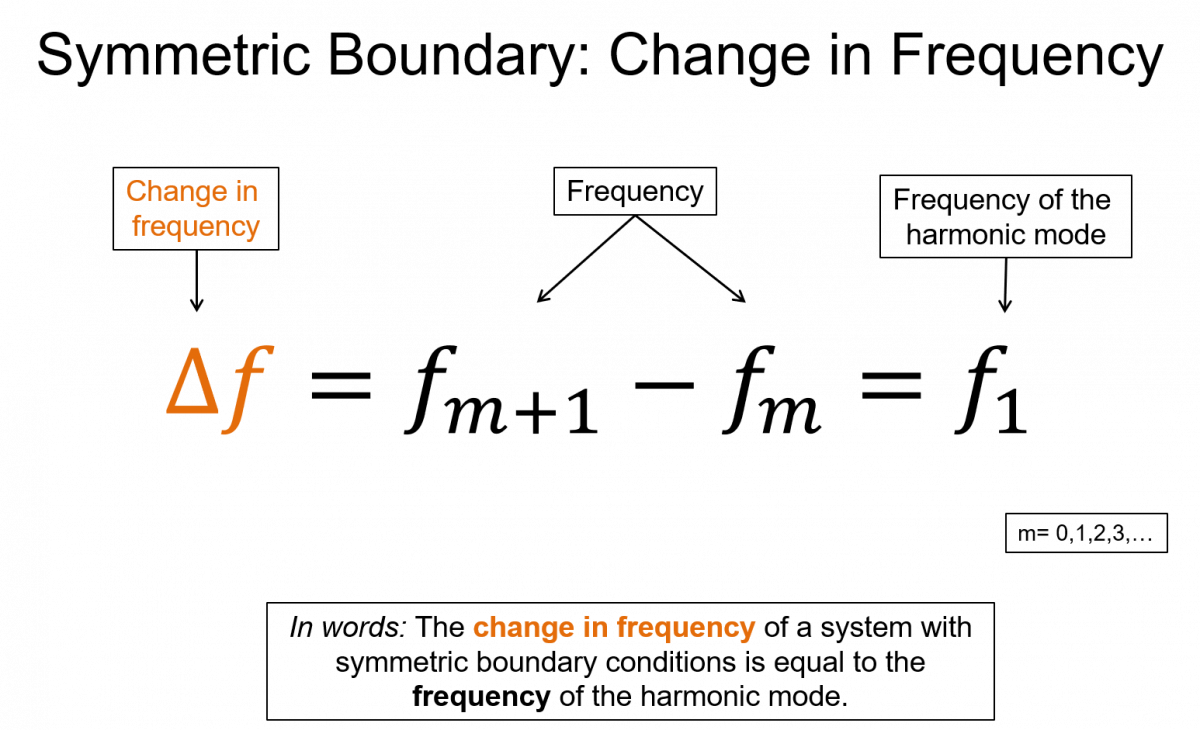


Graphical
Symetric boundary conditions.
Antisymetric boundary conditions
Descriptive
Standing waves are created by waves with the same frequency, wavelength, and ideally amplitude which are traveling in opposite directions. They add in such a way that it looks like the wave is just occilating up and down. However, the waves are still moving back and forth, but the contructive and destuctive interference of the two waves occur at fixed positions relative to the geometry of the system.
Experimental
Attach a rope so that one end is fixed, or have two people at each end of a rope. Now, move you hand up and down and find the correct frequency oscillation of your hand to create a standing wave. In the following video observe the motion of the persons hand as he creates several resonant standing waves. The first 2 minutes is important, otherwise please ignore the commentary as they use terminology that is not recommended.