Many of the empirical observation within the field of fluid mechanics lead to equations or laws that are dependent on the mass of the fluid or object being observed. Often times we cannot directly measure the mass but know information about the volume of the fluid or object. Thus we can use the material property called mass density to determine the mass of a given volume of material. The mathematical definition of mass density is...
$\rho = \frac{m}{V}$
In other words, mass density is mass per unit volume, and it is a material property (i.e. it is a constant for a given material).
*Note: There are other types of density (e.g. energy density, charge density, number density, area density, etc…). Since we will be working with mass density in fluid mechanics, we often drop the mass and just call it density.
Check out this video by Mark Drollinger highlighting 5 facts about density. Hopefully, this short video will demonstrate the importance of understanding mass density.
When a body of fluid is near a massive object such as the Earth, a pressure gradient within the fluid is formed. In this section we will quantify these pressure gradients by finding an expression for pressure at some depth below the surface of an incompressible fluid. We will also explore applications of Pascal’s law which tells us how a change in pressure within a an incompressible fluid is transmitted to other locations within the fluid.
The Science Nuts explain hydrostatics with a few quick everday examples, enjoy!
Pre-lecture Study Resources
Watch the pre-lecture videos and read through the OpenStax text before doing the pre-lecture homework or attending class.
BoxSand Introduction
Fluid Statics | Pressure
Consider comparing the differences between gold and Styrofoam (polystyrene foam). Perhaps you wish to compare the weight of two materials. Well, you can obtain one pound of gold and one pound of Styrofoam, so perhaps weight is not a good quantity when trying to compare the two materials. But now that you have a pound of each material, you notice that pound of gold takes up much less volume than the pound of Styrofoam. Cleverly, you define a new quantity called mass density, which is the mass per unit volume of each material. Mathematically this is written as…
$\rho = \frac{m}{V}$
It turns out, that the density is a material property. One pound of gold has the same density 2 pounds, 1,000 pounds, 1/100th of a pound, etc..
We must be a little bit more careful though. Consider water, if we place a container of water under enough pressure, we can slightly change the density. Likewise, if we change the temperature of a container of water, the density also slightly changes. Thus, the density of any material is dependent on temperature and pressure. However, for solids and liquids, the density is very nearly constant for a wide range of temperatures and pressure, thus throughout our fluid mechanics studies, we will ignore these small density variations due to temperature and pressure changes. Another way to state this approximation is to say that we will assume fluids are incompressible (i.e. their densities are constant for any temperature or pressure).
While standing on a horizontal patch of ice, the normal force that you apply on the ice is equal to the force of gravity from the earth on you ($m \, g$). The ice supports this normal force no matter how you stand on the ice (e.g. lay down or stand with high heels on). However, you might already known that you would feel much more comfortable lying down on thin ice than standing with high heels on. Even though the ice is supporting the same weight ($m \, g$), the ice is more likely to break if you wear the high heels, thus we must introduce a new quantity to differentiate between these two scenarios. The new quantity introduced is called pressure. Pressure is defined as the perpendicular component of force divided by the area that the force is applied to. Mathematically this is written as…
$P = \frac{F_{\perp}}{A}$
Notice how it is only the perpendicular component of force. Since area is a scalar and the perpendicular component of force is a scalar, then pressure must also be a scalar.
The SI unit for pressure is $\frac{N}{m^2}$, which is given a special name called a Pascal (Pa).
$1 Pa = 1 \frac{N}{m^2}$
*NOTE: Pressure is often written as $P = \frac{F}{A}$, where it is implied that the force is only the perpendicular component.
Pressure plays an important role in fluid mechanics because pressure differences cause an associated net force.
$pressure \, difference \Longrightarrow \sum{\vec{F}}$
As we will see in the hydrostatics section, there exists a pressure gradient within a fluid near a massive object like the Earth - the pressure increases the deeper you go in the fluid. So pressure and the associated net force due to pressure differences are the foundations upon which we will build our fluid mechanics models.
Atmospheric pressure ($P_{atm}$)
We live in a mixture of gasses (the atmosphere) that surrounds us in all directions. Consider a column of atmosphere directly above us. This column of atmosphere has an associated weight, and just like our ice example, this atmospheric weight is supported by the surface of the Earth, or our heads as we stand on the Earth’s surface. Thus if we consider the force that this column of atmosphere applies over the area of the column, we can define a pressure due to the atmosphere near the Earth’s surface. The actual atmosphereic pressure is complicated, depending on temperature, height, humidity, etc… However, at sea level in standard conditions according to the International Standard Atmosphere model (ISA), the standard atmosphereic pressure is $101.325 \, kPa$. This value is also defined as 1 atmosphere ($atm$).
$1 \, atm = 101.325 \, kPa$
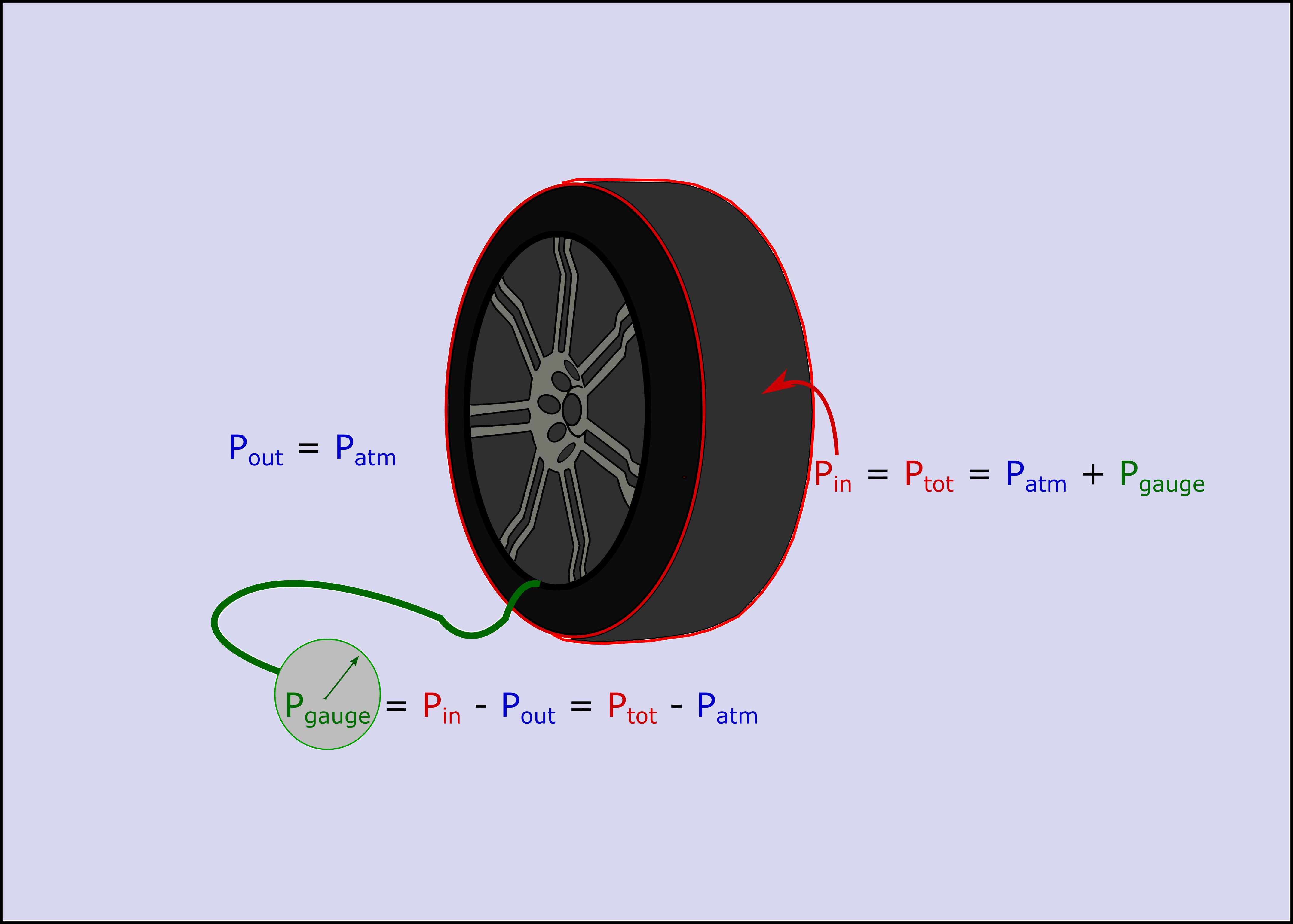
Gauge pressure ($P_{g}$)
The devices we use to measure pressure within a closed container often measure the pressure difference between the inside of a container and the outside. For example, if you use a tire pressure gauge to measure the pressure in your car tires, you are really measuring the difference between the outside atmosphereic pressure and the total pressure inside the tire (as seen in the figure below).
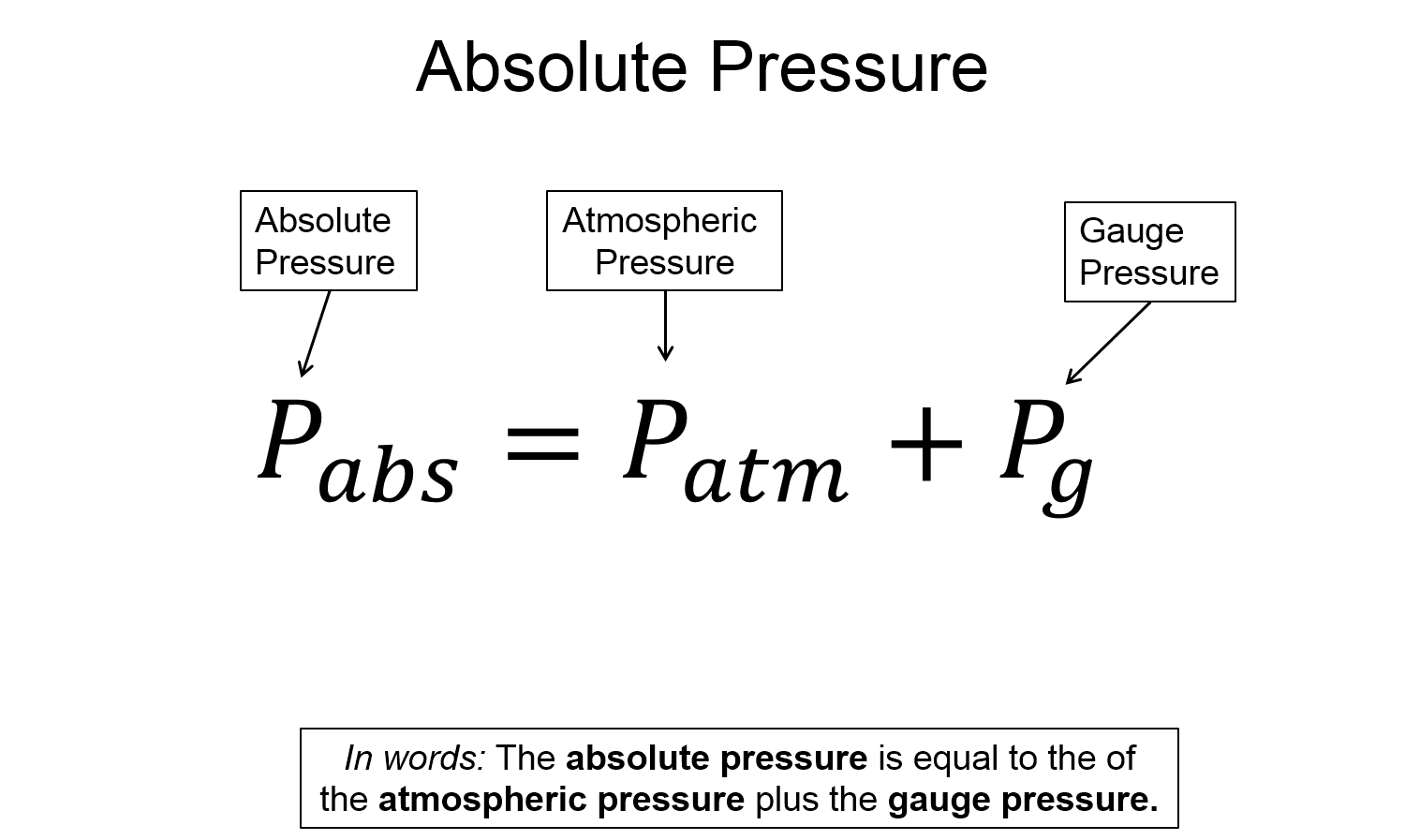
Absolute pressure ($P_{abs}$)
The absolute pressure is then the sum of the atmospheric pressure and gauge pressure.
$P_{abs} = P_{atm} + P_{g}$
Pressure at a depth
Have you ever gone swimming in a really deep body of water? If so, you are probably familiar with the sensation you get when diving down to very deep depths below the surface of the water. This sensation is a result of your inner ears letting you know the pressure of the water around you is increasing. How can we mathematically show this pressure increase as we go deeper into the water, also referred to as “pressure at a depth”?
Consider a container of water open to the atmosphere at the top as shown in the figure below.
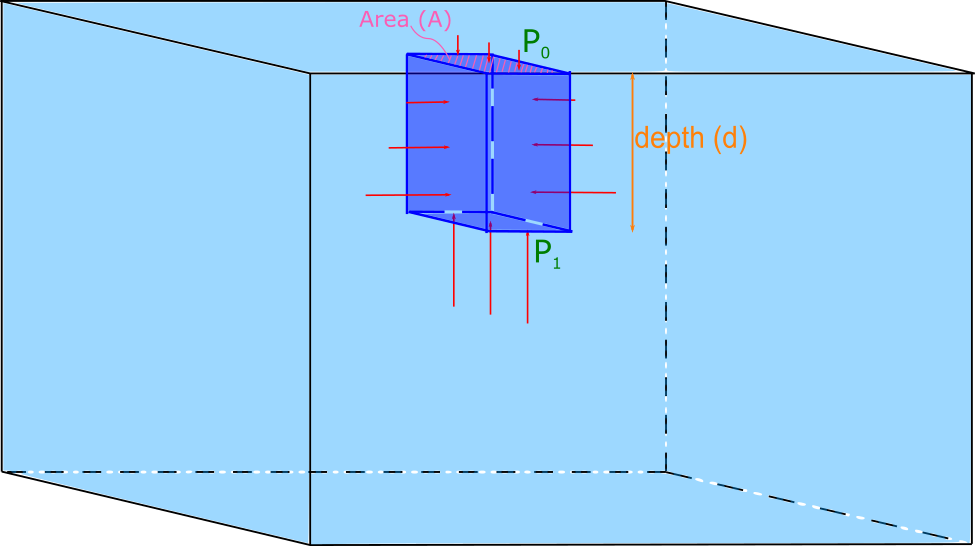
Let the density of the water be $\rho_f$. Now imagine a smaller rectangular volume element of water in the container as indicated by slightly darker blue. The downward force on this volume element of water at the top of the surface is due to the atmospheric pressure $P_0$ multiplied by the area $A$ of the top of the volume element. Since this volume of water is stationary, (i.e. it is not accelerating), we know that there must be an upward force at the bottom of the volume element which is greater than the top force because it must also support the weight of the volume element. This statement is analgous to the following situation: 5 books are stacked on top of each other, the top book has a normal force acting on it upwards from the second from the top equal to the weight of the top book only, while the book on the bottom of the stack has a normal force acting on it upwards from a table equal to the combined weight of all 5 books. There are also forces from the pressure on either side (left, and right) of the volume element which must be equal to each other because the volume element is not accelerating in either direction. The descriptive representation of this scenario is nicely visualized with an accompanying FBD for the volume element of water as shown below. (The horizontal forces are not shown since they all cancel out.)
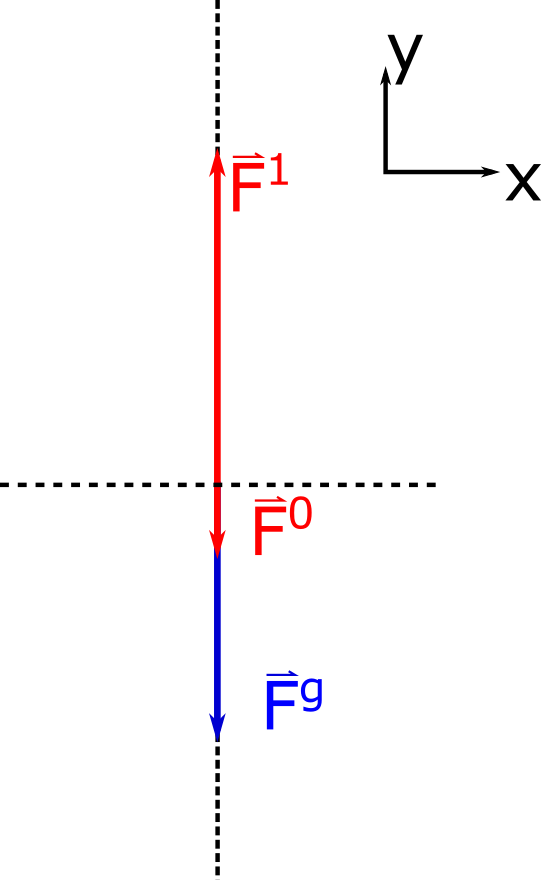
Using Newton's second law we can translate our physical representation (FBD) into a mathematical representation as shown below.
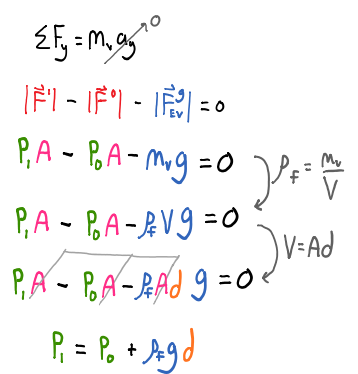
Notice the end result for the pressure at the bottom of the volume element is not dependent on the area or volume, it only depends on the depth below the surface $d$, the density of the fluid $\rho_f$, the acceleration due to gravity caused by the planet the body of fluid is near $g$, and the pressure above the surface of the fluid $P_0$.
*NOTE: Our analysis of pressure at a depth used the assumption that the fluid is incompressible (i.e. the fluid has a constant density). This is a good assumption for liquids like water that do not compress much. In contrast, the atmosphere is still considered a fluid, but it is a gas which is easily compressible, thus our pressure at a depth analysis is only valid for very small depths.
Pascal's law
Pascal's law is formally stated as follows, "for an incompressible and enclosed fluid, a change in pressure at one location results in the same change in pressure, without a diminish in magnitude, at all locations within the enclosed fluid and walls".
Key Equations and Infographics
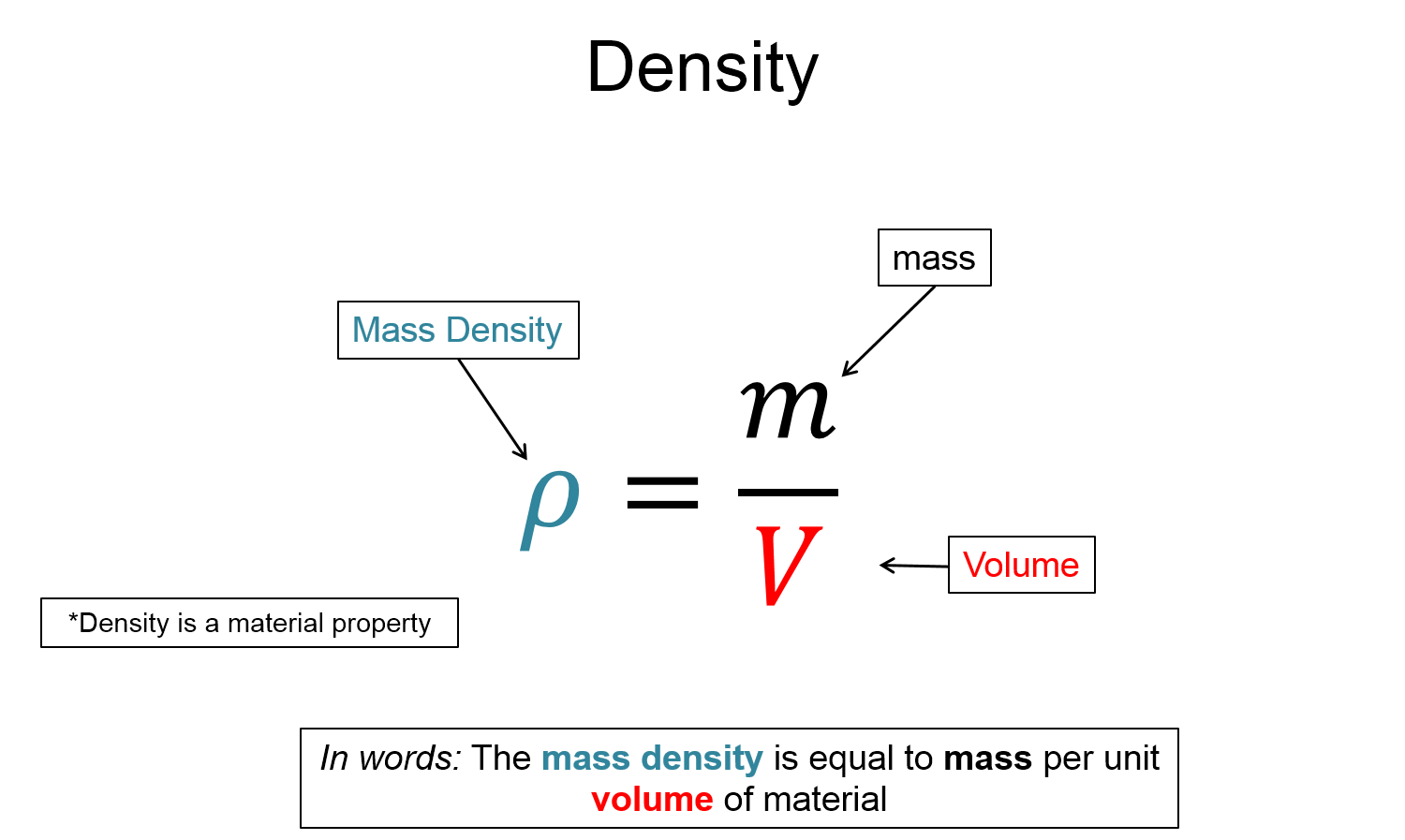


Now, take a look at the pre-lecture reading and videos below.
BoxSand Videos
Required Videos
definitions, pressure, density(2min)
Atmosphere ... needs density gradient explanation with thermo..... (5min)
Suggested Supplemental Videos
OpenStax Reading
OpenStax Section 11.1 | What is a Fluid?
OpenStax Section 11.2 | Density
OpenStax Section 11.3 | Pressure
OpenStax Section 11.4 | Variation of Pressure with Depth
OpenStax Section 11.5 | Pascal's Principle
OpenStax Section 11.6 | Gauge Pressure, Absolute Pressure, and Pressure Measurement
Fundamental examples
1. The largest gold bar easily available for an individual to purchase has dimensions of about $3.15$ inches by $1.58$ inches by $0.71$ inches ( length x width x height). What is the mass of this gold bar? The density of gold is about $19,320 \, kg / m^3$.
2. Your goal is to make 12 gauge copper speaker wire (cylindrical cable with a diameter of about $2.05232 \, mm$. What is the length of wire you can produce if you start with $0.5 \, kg$ of copper?
CLICK HERE for solutions.
Short foundation building questions, often used as clicker questions, can be found in the clicker questions repository for this subject.
1. Estimate the pressure you exert on a horizontal surface while standing still.
2. If the pressure inside a tire at sea level in standard conditions is $335.747 \, kPa$, what is the value a tire pressure gauge would read?
3. Consider a closed container with a $10 \, kg$ piston of diameter $8 cm$ which is free to move vertically as shown in the image below. (a) If the piston is stationary, and the outside is at standard atmospheric pressure, what must the pressure inside the container be? (b) If you used a pressure gauge, what what the gauge read?

CLICK HERE for solutions.
Short foundation building questions, often used as clicker questions, can be found in the clicker questions repository for this subject.
Post-Lecture Study Resources
Use the supplemental resources below to support your post-lecture study.
Practice Problems
BoxSand Practice Problems (SOLUTIONS)
Conceptual problems
BoxSand's multiple select problems
BoxSand's quantitative problems
Recommended example practice problems
- Openstax section on density has practice problems at the bottom, Website Link
- 8 problems, strictly density, PDF Link
For additional practice problems and worked examples, visit the link below. If you've found example problems that you've used please help us out and submit them to the student contributed content section.
BoxSand practice problems
Conceptual problems
BoxSand's multiple select problems
BoxSand's quantitative problems
Recommended example practice problems
- Openstax section on pressure has practice problems at the bottom, Link
- 6 Questions, strictly pressure, PDF Link
- 4 Questions, pressure and Pascal's Principle, PDF Link
For additional practice problems and worked examples, visit the link below. If you've found example problems that you've used please help us out and submit them to the student contributed content section.
Additional Boxsand Study Resources
Additional BoxSand Study Resources
Learning Objectives
Summary
Summary
Atomistic Goals
Students will be able to...
YouTube Videos
The Boundless text section on Pressure.
Hyperphysics covering pressure
Other Resources
This link will take you to the repository of other content related resources .
Clear and easy to understand video describing pressure
https://www.youtube.com/embed/7m7J5T7c6ig?rel=0
Doc Schuster lecture on pressure
https://www.youtube.com/embed/bmEwTaJpRh8?rel=0
AP Physics lecture on Pressure and Pascal's Principle, includes basic examples throughout
https://www.youtube.com/embed/MK_cG85iOO4?rel=0
Other Resources
This link will take you to the repository of other content related resources .
Simulations
This PhET simulation allows you to play around with different materials in a puddle, seeing how their density effects their ability to stay afloat.
If you are on a Windows PC you should download and run this simulation, which allows you to mix fluids of different densities and then float balloons filled with different fluids in your stack of fluids
For additional simulations on this subject, visit the simulations repository.
Use the Colorado PhET pressure simulation below to learn more about how pressure works.
For additional simulations on this subject, visit the simulations repository.
Demos
What happens to water flowing from a container that is put into free-fall?
For additional demos involving this subject, visit the demo repository
For additional demos involving this subject, visit the demo repository
History
Oh no, we haven't been able to write up a history overview for this topic. If you'd like to contribute, contact the director of BoxSand, KC Walsh (walshke@oregonstate.edu).
Physics Fun
The Weather Channel uses density to demonstrate the movement of cold air.
Pressure difference drawing up the fluid

Other Resources
Resource Repository
Page by the United States Geological Survey on Density
The HyperPhysics reference for density is short sweet and too the point.
This website seems to be centered around geoscience and gives a great one page coverage of density
Other Resources
This link will take you to the repository of other content related resources for impulse.
The Boundless text section on Pressure.
Hyperphysics covering pressure
Other Resources
This link will take you to the repository of other content related resources .
This link will take you to the repository of other content related resources.
Problem Solving Guide
Use the Tips and Tricks below to support your post-lecture study.
Assumptions
When working we fluids, we typically assume incompressibility, which means that the fluid doesn't compress at all under pressure. This is a good approximation for many fluids, including water. A consequence of this is that if pressure is exerted on a fluid (say with a piston) it will push in every direction with equal pressure to that exerted on it.
As also assume the fluid has no internal resistance to movement (viscosity), the molecules have no interaction with each other, and neglect many aspects that typically concern practice applications of fluids like surface tension, eddy currents, energy and force lost to rotating liquid molecules. The study of fluid mechanics is highly complicated because there are a lot of different and not easily defined properties to fluids that aren't as much of a problem when studying gases or solids.
Most aspects of fluid dynamics are beyond the scope of this course and fully realized descriptions of how fluids move and work in the real world can usually only be approximated through computer simulations given that their movement is highly non-ideal and difficult to do regular calculations with. With this in mind, we restrict our discussion of fluids to focus on macro aspects of fluids, such as volume and pressure, and make idealizing assumptions, that turn out to be pretty accurate for most fluids, freely that make them analytical. While this aspect is true for most areas of physics we have studied, for fluids it is more true than ever.
Checklist
1. Read and re-read the whole problem carefully.
2. Visualize the scenario. Mentally try to understand what the problem is asking (think about the geometry, such as cylinders, cubes, spheres, etc.. that the problem might be asking about).
3. Draw a physical representation of the scenario, this may include a picture of an object with labeled dimensions.
4. Identify all the knowns and unknowns.
5.a. Start with the definition of mass density $\rho = \frac{m}{V}$. OR
5.b. Start with the definition of pressure $P = \frac{F_{\perp}}{A}$.
a. Identify which quantities you know and don't know.
b. Use the geometry of the object and subsitute the definition of volume for that specific shape if necessary.
6. Carry out the algebraic process of solving the equation.
7. Evaluate your answer, make sure the units are correct and the results are within reason.
Misconceptions & Mistakes
- Densities are often given in terms of $g/cm^3$. Be careful when looking up these values. It is recommended to always use SI units ($kg, m, s$).
- The density of materials can change, but solids and liquids change by vary small amounts thus we ignore these changes and assume that the densities are constant for a wide range of pressures and temperatures.
- Since we only use the perpendicular component of force, pressure is a scalar. Be sure to only use the perpendicular component of force.
- Absolute pressure can not be negative, but gauge pressure can be negative.
- The net force due to a pressure gradient is not the overall net force of an object, there may be other forces acting on the object you must account for.
Pro Tips
- When trying to find the volume, mass, or density of an object, draw a picture of that object and label all dimensions. This will help you visualize the geometry of the problem.
- When trying to find the volume, mass, or density of an object, draw a picture of that object and label all dimensions. This will help you visualize the geometry of the problem.
Multiple Representations
Multiple Representations is the concept that a physical phenomena can be expressed in different ways.
Physical
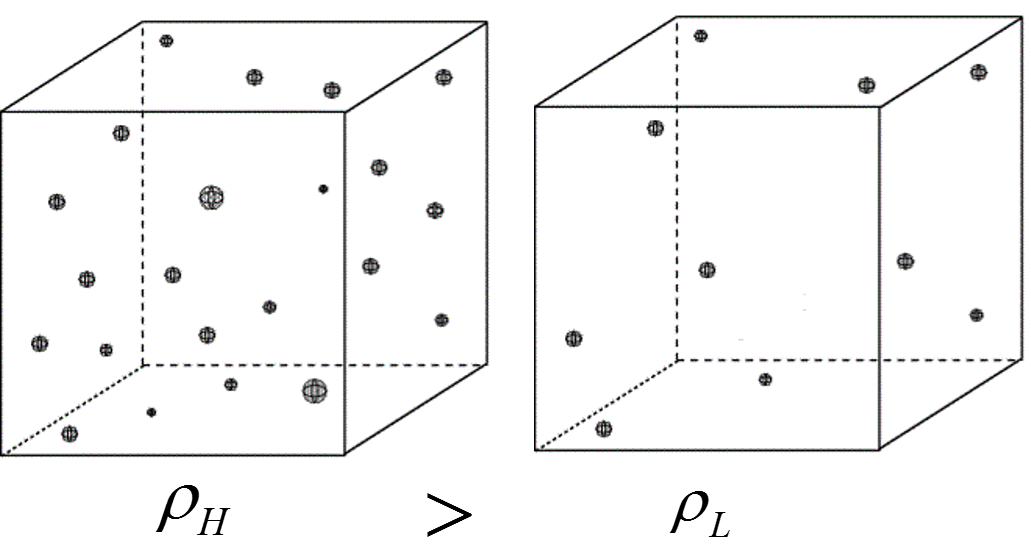
Since there are more particles in the left box, the density inside the left box is higher.
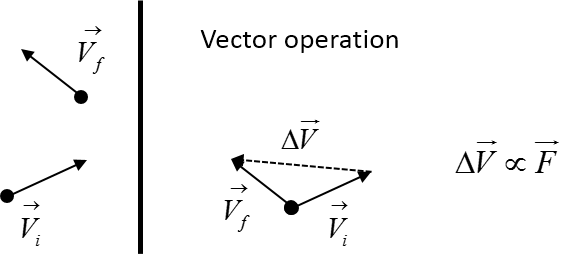
The change in velocity is of a particle is directly proportional to the force. We have a partilce that collides with a wall. The force on the particle due to the impact is equal and opposite. Imagine the wall bleow is part of a container, the higher the velocity of the impacting particle the greater the force. In turn this means a higher pressure inside the container.
Mathematical
$\rho = \frac{m}{V}$
Volume mass density ($\rho$), Mass ($m$), Volume ($V$)
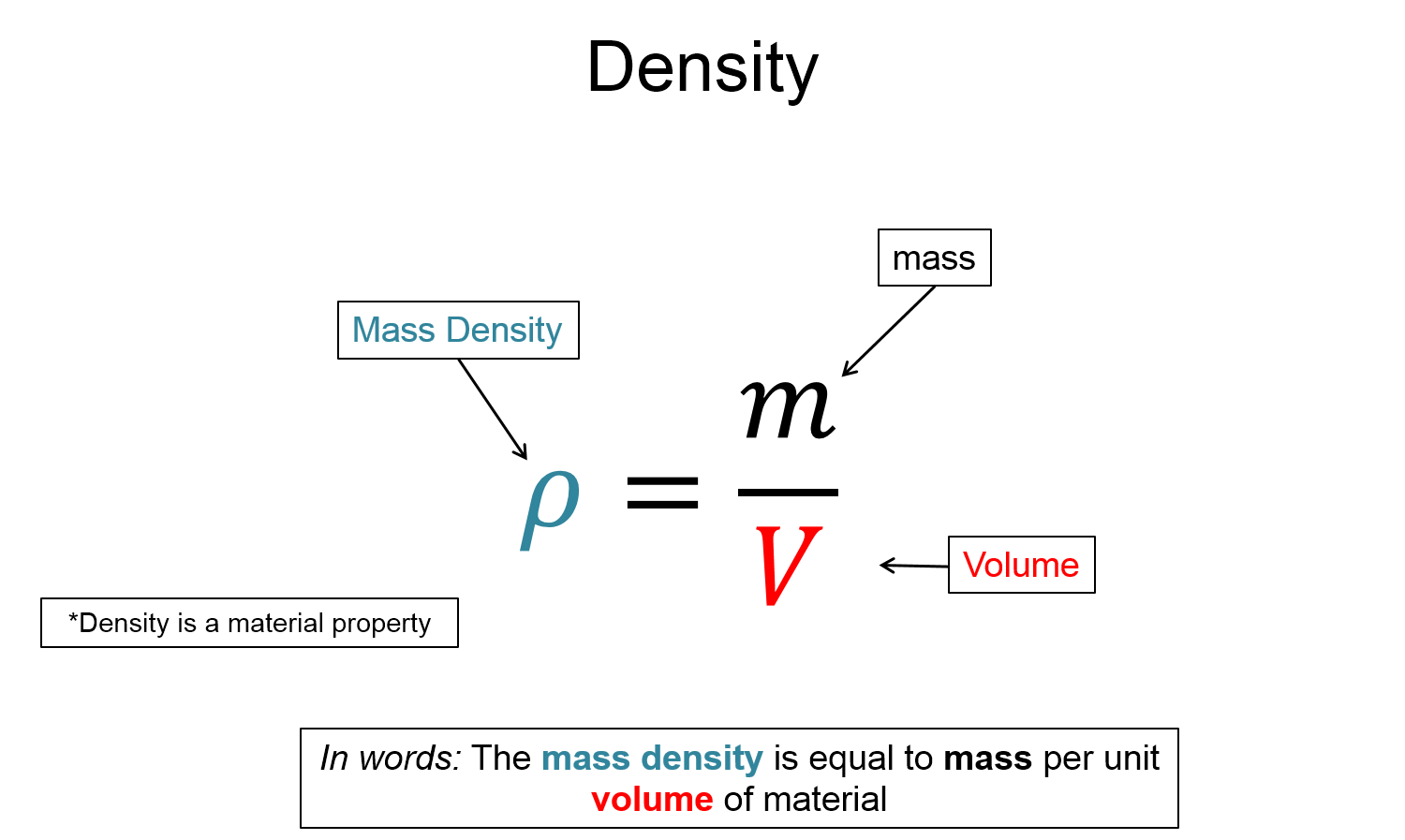
$P = \frac{F}{A}$
Pressure (P), Force (F), Area (A)

Graphical
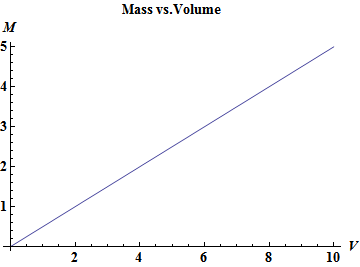
The following plots the mass vs the volume where the slope of the line is the density $\rho$.
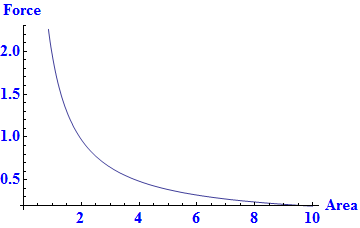
Pressure is force per area. The plot below describes pressure relative to force and area.
Descriptive
The density of a material is dependent on the ratio of the total mass of the material and the volume of the material.
Pressure is the total force (F) per area (A).
Experimental
The following video is a layering density experiment where various objects and liquids are poured in to a column to demonstrate varying densities.
If we submerge and empty water bottle into a bath of hot water the bottle will expand. This is due to the increased pressure inside of the bottle. The air molecules are excited due to the increased temperature of the internal temperature of the bottle thus increasing the kinetic energy of the air molecules which collide with the walls of the water bottle at a higher velocity, thus increasing the amount of force applied to the inner surface area of the bottle.