Matter comes in three main states, solids, liquids, and gases. The kinetic theory of gases models a gas as a collection of seldom interacting particles, flying around in random directions. The molecules of the gas have a range of speeds, due to their occasional interaction. For a complete energy analysis this motion of the particles of the gas needs to be accounted for. Thermal energy is what we call the summation of all the individual kinetic energies of the molecules of the gas. As the kinetic energy increases, the temperature increases. The kinetic theory connects the average speed of the particles with the temperature and kinetic energy.
Check out this quick introduction to kinetic theory from Doodle Science.
Pre-lecture Study Resources
Watch the pre-lecture videos and read through the OpenStax text before doing the pre-lecture homework or attending class.
BoxSand Introduction
Thermodynamics | Kinetic Theory of Gasses
The Kinetic Theory of Gases is an important model that paves the way for connecting a very microscopic view of matter to the very macroscopic measurements we make. The model treats a gas as a collection of microscopic particles traveling with a distribution (Maxwell-Boltzman) of speeds, all moving in random directions, bouncing off each other and the walls of the container holding the gas. The distribution of speeds is specific to a given macroscopic temperature.
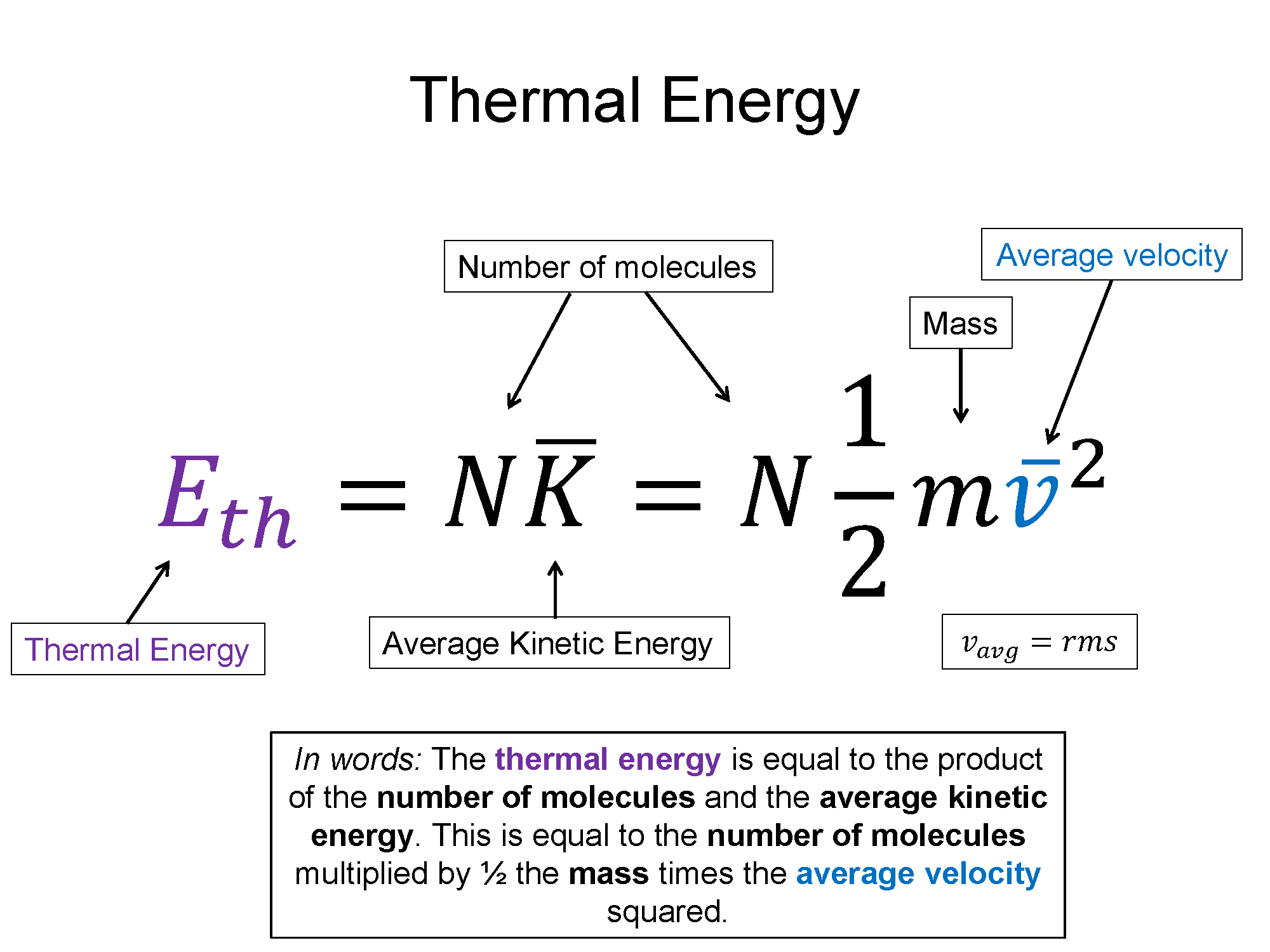
Each of these particles possess kinetic energy ($\frac{1}{2}m v^2$) and if you add up the total kinetic energy of each particle you get a new form of energy, thermal energy ($E_{th}$). Since accounting for 1026 particles all with different speeds is impossible, we will instead employ the use of averages. In the equation below $\overline{K}$ is the average kinetic energy per particle.
$\overline{K} = \frac{1}{2}m^*v_{rms}^2$, where $m^*$ and $v_{rms}$ are the average mass and speed per particle
Technically $v_{rms}$, where the rms stands for root mean square, is a more complicated statistical average, but for the sake of this discussion you can simply think of it as an average speed. From here down I'll just write it as m and v, but realize they are the average of those quantities. If you have N number of particles then you have a total thermal energy of:
$E_{th}=N\overline{K}=N \frac{1}{2}mv^2$
All of this is well and good but we still haven't made any connection to the macroscopic world and real measurable - after all we can't shrink down to the size of a molecule and start using our radar gun to measure a bunch of particle speeds. That's where a bold postulate was formed by a physicist named Boltzman where he imagined each degree of freedom the particles have contribute $\frac{1}{2}k_B T$ to the total energy. Here $k_B$ is Boltzman's constant (the real heart of the micro/macro connection) and T is temperature measured in Kelvins. Degrees of freedom are related to the ways a particle can move. For a mono-atomic gas (bunch of individuals "balls") the particles can move in x, y, and z, but do not have any appreciable rotation or vibration. So for a mono-atomic gas the degrees of freedom (D) is equal to 3. Contrast this to a diatomic gas, where I picture two balls connected by a spring, so they collection can still move in x, y, and z, but they can also rotate about each other and vibrate towards then away from each other. This means they would have a degree of freedom higher than 3, most likely near 5. More complex molecules will have higher degrees of freedom which results in more ways to store energy without changing linear kinetic energy of the molecule. For this discussion though we will stick to mono-atomic gases. So, thermal energy can be written in the following way:
$E_{th}=N D \frac{1}{2} k_B T$
which for a mono-atomic gas with D = 3, is $E_{th}=N\frac{3}{2}k_B T$
Combine the microscopic view of particle speeds above with Boltzman's view of a macroscopic observable like temperature, and you get a fundamental connection between the two views.
$E_{th}=N\frac{1}{2}m v^2 = N \frac{3}{2}k_B T$, mono-atomic gas
Equilibrium: If there is a different average kinetic energy in one part of the container than in the another, the system will not be in equilibrium and will drive towards a constant average kinetic energy throughout the container. Once equilibrium has been obtained, average kinetic energy is constant, and thus temperature is also constant. It's important to think in terms of energy gradients cause systems to want to change. In this case the measurable that drives towards being constant is temperature.
Key Equations and Infographics


Now, take a look at the pre-lecture reading and videos below.
BoxSand Videos
Required Videos
Microscope View of States of Matter (10 min)
Thermo State Variables (2 min)
State Variable: Pressure (5 min)
State Variable: Volume (1 min)
State Variable: Number (1 min)
Suggested Supplemental Videos
OpenStax Reading
OpenStax Section 13.1 | Temperature
OpenStax Section 13.4 | Kinetic Theory: Atomic and MOlecular Explanation of Pressure and Temperature
Fundamental examples
1. A given atom in a gas of monatomic helium atoms has an average kinetic energy $\bar{K} = 2.07 \times 10^{-21}J$. (a) What is the $v_{rms}$ of these atoms? (b) What is the temperature of this system?
2. Which contains more moles: $100 \hspace{0.1cm} g$ of Hydrogen gas or $400 g$ of water?
3. Imagine you have an insulated box with a semi-permeable membrane in the middle. The membrane allows heat transfer across it, but does not allow particles to pass through it. You have a probe that tells you that particles on the right-hand side of the box happen to have an average kinetic energy of $\bar{K_1} =4*10^{-21}$ Joules, while particles on the left-hand side have an average kinetic energy of $\bar{K_2} = 8*10^{-21}$ Joules. There are $10^{10}$ monatomic particles in each half of the box. Calculate the thermal energy in the left side and right side of the box $E_{th,l}$ and $ E_{th,r}$. How will $E{th,l}$ and $E_{th,r}$ change as the system tends toward equilibrium?
4 (synthesis problem, slightly more challenging). You have a monatomic gas with $N=10^{23}$ particles and an initial thermal energy of $E_{th,i} = 1 kJ$. (a) What is the initial temperature of the gas? (b) You have an engine that converts chemical energy (ie. the energy found in food) into heat with 100% efficiency. You want to raise the temperature of your gas, so you hook this engine up to your monatomic gas and feed it a delicious 800-Calorie lamb gyro. What is the new temperature of the gas?
Short foundation building questions, often used as clicker questions, can be found in the clicker questions repository for this subject.
Post-Lecture Study Resources
Use the supplemental resources below to support your post-lecture study.
Practice Problems
BoxSand's multiple select problems
BoxSand's quantitative problems
Recommended example practice problems
- Openstax, bottom of the page, 10 questions (including the conceptual question) Website Link
- Good set of problems which includes a bit a review at the top, PDF Link
(Contains only answers, no solutions)
For additional practice problems and worked examples, visit the link below. If you've found example problems that you've used please help us out and submit them to the student contributed content section.
Additional Boxsand Study Resources
Additional BoxSand Study Resources
Learning Objectives
Summary
Summary
Atomistic Goals
Students will be able to...
Microscopic view of matter
- (UPMF) Construct a microscopic model of a solid using an analogy of particle masses connected by springs.
- Construct a microscopic model of a liquid as a collection of loosely bonded masses able to roll around each other.
- Construct a microscopic model of a gas consisting of a set of rarely interacting particles.
- (UPMF) Construct a model of microscopic particle interactions arising from electromagnetic forces.
Macroscopic view of matter
- Employ the fact that solids retain their shape unless deformed by a relatively large force.
- Employ the fact that a liquid in a gravitational field will take the shape of a container when poured into it.
- Employ the fact that a gas expands to distribute itself in the container it occupies.
- Distinguish between the density of solids, liquids, and gasses.
- Define pressure as a perpendicular force component per area.
- Define volume as having dimensions of length cubed.
- Explain how density and compressibility are related.
- Distinguish between the compressibility of solids, liquids, and gasses.
- Identify when the constant density and compressibility approximation breaks down (e.g. water at the bottom of the ocean).
Connecting Microscopic and Macroscopic views of matter
Kinetic theory of monatomic gases
Equations of state and state variables
Ideal gas law
- Demonstrate that the macroscopic state of the system arises from a microscopic ensemble of particles.
- Construct a model where an ensemble of microscopic particles' kinetic energy results in a macroscopic overall temperature.
- Construct a model of pressure arising from an ensemble of microscopic particle collisions, where momentum in transferred, resulting in a macroscopic force per area.
- Demonstrate that the average microscopic kinetic energy of a particle is a function of the average mass and average (root mean squared) speed.
- Demonstrate that the total thermal energy of a system is the sum of the microscopic translational kinetic energy of all the particles.
- Identify three modes of microscopic kinetic energy: translational, vibrational, and rotational.
- Show that a monatomic gas only possess the translational mode of kinetic energy.
- Apply the Boltzmann postulate to connect the microscopic translational kinetic energy to macroscopic observable of temperature.
- Show that the total thermal energy is a function of total number of particles and temperature of the gas.
- Convert between number of particles and number of moles using Avogadro's number.
- Convert between number of particles and number of moles using the gas constant R and Boltzmann's constant kB.
- Differentiate between open, closed, and isolated systems, and how they apply to the exchange of energy and particle number between systems.
- Explain that state variables are quantities that characterize the thermodynamic state of a system and are used to construct the equation of state.
- Explain that an equation of state is a function that relates state variables and defines the state of the system in equilibrium.
- Differentiate between extrinsic and intrinsic state variables, where extrinsic scales with the number of particles and intrinsic does not.
- Define pressure, volume, number of particles, and temperature as state variables.
- Explain that there are other state variables including thermal energy, chemical potential, entropy, magnetization, degrees of freedom(?), … etc.
- Identify that the ideal gas law is an equation of state that contains the state variables, pressure, volume, temperature, and number of particles.
- Define a system as an ideal gas if (i) it has particles that do not interact with each other or (ii) all interactions are elastic collisions.
- Recognize an ideal gas is an assumption not always relevant.
- Identify when a system can be approximated as an ideal gas by justifying the density as sufficiently low so collisions are rare, or the particles making up the gas are not easily deformed.
- Recognize that there are more sophisticated equations of state to account for increasingly complicated intrasystem interactions, such as the Van der Waals equation of state that accounts for particle size and polar interactions.
- Apply proportional reasoning using the ideal gas law.
- Describe the features of an inverse relationship, i.e. pressure and volume at constant number of particles and temperature.
PV-diagrams
- Interpret a plot of pressure vs. volume where each point on the plot represents a different equilibrium state of the system.
- Construct and interpret a PV-diagram for a given equilibrium state of a system, or changes in the state of the system between two equilibrium points.
YouTube Videos
Pre-Academy does a great job of introducing the subject of kinetic theory.
Khan Academy discusses the kinetic moelcular theory of gases.
PBS Crash Course physics tackles kinetic theory and phase changes.
This video gives a good overview of Kinetic Theory of gases as well as an example.
Doc Schuster covers the kinetic theory of gases.
Other Resources
This link will take you to the repository of other content related resources.
Simulations
This shows the distribution of velocities for a gas comprised of different molecules.
This is a interactive simulation showing how pressure increases kinetic interaction. Be sure to click all boxes on the lower left hand corner of the applet.
For additional simulations on this subject, visit the simulations repository.
Demos
Check out these experiments involing the kinetic molelcular thoery of gases.
For additional demos involving this subject, visit the demo repository
History
Oh no, we haven't been able to write up a history overview for this topic. If you'd like to contribute, contact the director of BoxSand, KC Walsh (walshke@oregonstate.edu).
Physics Fun
Other Resources
Hyperphysics provides a useful reference for kinetic theory
Theses slides cover kinetic theory of gases quite well with examples problems,
Another textbook covering of kinetic theory.
Resource Repository
This link will take you to the repository of other content related resources.
Problem Solving Guide
Use the Tips and Tricks below to support your post-lecture study.
Assumptions
While often forgotten while solving problems, the kinetic theory requires the assumptions of a large number of gas particles at relatively low pressures and high temperatures. This hits on the concept of what an "ideal gas" is. Basically, if you put a gas under too much pressure, it starts to become like a liquid because the particles are forced closer together due to high pressure, eventually becoming solid-like if the pressure gets high enough. Likewise, if you lower its temperature too much, it will phase change into a liquid as well from loss of energy. Therefore, ideal gases, i.e. the gases for which the kinetic theory of gases is valid, depend on the assumptions that the gases are at sufficently low pressure and high temperature. We also assume that the particles themselves have neglibible volume (or we'd have to subtract out the volume of these particles) and that they will not interact with each other, only with the walls of their container! If you're interested in what we do to account for these in more percise physics, look up the Van Der Waals equation, it is the ideal gas law that considers these effects! Although, in practice, you can assume ideal gases for all of our problems in this class!
Checklist
General Summary:
Problems in the Kinetic Theory of Gases typically involve systems coming to thermal equilibrium. That means it is important to keep the main qualitative concepts of this section in mind when solving a problem:
- Temperature is a measure of the average kinetic energy of a group of atoms ($\bar{K} \propto T$)
- The thermal energy of a gas of atoms is proportional to the average kinetic energy ($ E_{th} \propto \bar{K}$)
- Therefore Temperature is a value that represents the thermal energy of an ensemble of particles (in this case a gas of atoms) ($T \propto E_{th}$
Two systems with different temperatures that come into thermal contact with each other will approach thermal equilibrium. This means energy will flow down a thermal energy gradient from regions of higher temperature to regions of lower temperature until all regions that are in thermal contact with one another have the same temperature.
The speed of a particle can be approximated by finding the rms velocity $v_{rms}$. Since thermal energy is proportional to kinetic energy and kinetic energy is proportional to $v_{rms}^2$, the $v_{rms}$ tells you something about the temperature of a particle.
Solving Problems
1. We only make use of a handful of variables in this section (mostly $\bar{K}$, $T$, $E_{th}$, $m$ and $N$ (or $n$)), so try to keep a careful inventory of those values. Likewise, at this point we only really have a handful of equations at our disposal, the following being the main two:
$E_{th} = D \frac{1}{2}N k_B T = D \frac{1}{2} nRT$ (1)
$E_{th} = N\bar{K} = N \frac{1}{2} mv^2$ (2)
Most problems in this section will focus on questions that can be answered with a single calculation if you have taken an inventory of your variables
2. Because there are so few variables/equations, questions in this section tend to be more qualitatively challenging. This means you need to read every problem very carefully to find hints about things like whether the gas is monatomic or diatomic, or if two systems are in thermal contact with one another.
3. Most problems in this section focus on systems coming to thermal equilibrium, or properties of gasses that are in thermal equilibrium with their surrounding, so it is imperative to understand the implications of thermal equilibrium (i.e. systems in thermal equilibrium share a temperature and no heat flows between them).
Misconceptions & Mistakes
Pay attention to pressure gauges and gauge pressures. Usually, they will subtract off atmospheric pressure, because practically for things like car tires, we only car about the pressure difference between the air inside the tire and the air outside (the air inside the tire being at higher pressure than the atmosphere allows the tire to remain tout and inflated). To get the absolute pressure (the P that shows up in most of our equations), you need to take the gauge pressure and ADD the pressure of the atmosphere onto that pressure. The pressure of the atmophere is approximately 101,300 Pa at sea level (we assume we're near sea level typically).
Temperature is a measure of the thermal energy of an ensemble of particles. Temperature and Heat are not synonymous. Temperature is a global property of a gas, since it reflects energy of many particles, an entire system can be associated with a temperature. Heat is a form of energy that we use to show the transfer of thermal energy between different parts of a thermodynamic system. In short, temperature is a property of a system that corresponds to the total thermal energy in that system, heat is a type of energy that transfers between thermodynamic systems.
Pro Tips
- The degrees of freedom of an atom or a molecule is an important concept. $D$ essentially tells you how much energy an atom or molecule can hold at any particular temperature. This means that if you are considering two molecules at the same temperature, one monatomic and one diatomic, the diatomic one will have more energy just by virtue of having additional degrees of freedom.
- If you're asked about the "speed of a particle," you are really being asked for the root-mean-squared (rms) speed: $v_{rms} = \sqrt{\frac{3k_B T}{m}}$
- Near STP, most gasses you encounter will behave according to the kinetic theory of gasses. It is only once you get to very exotic temperatures, pressures, concentrations, and charges that the kinetic theory of gasses starts to lose its predictive value and you need to start considering other physics (like statistical mechanics or quantum mechanics).
- Average kinetic energy comes from the statistical definition of the mean. This means that if you select a particle at random and measure it with your Magical Kinetic Energy Measurer Probe, it will not necessarily have the average kinetic energy. But, if you made many measurements of many particles, you will find a standard distribution of velocities centered on the mean value.
Multiple Representations
Multiple Representations is the concept that a physical phenomena can be expressed in different ways.
Physical
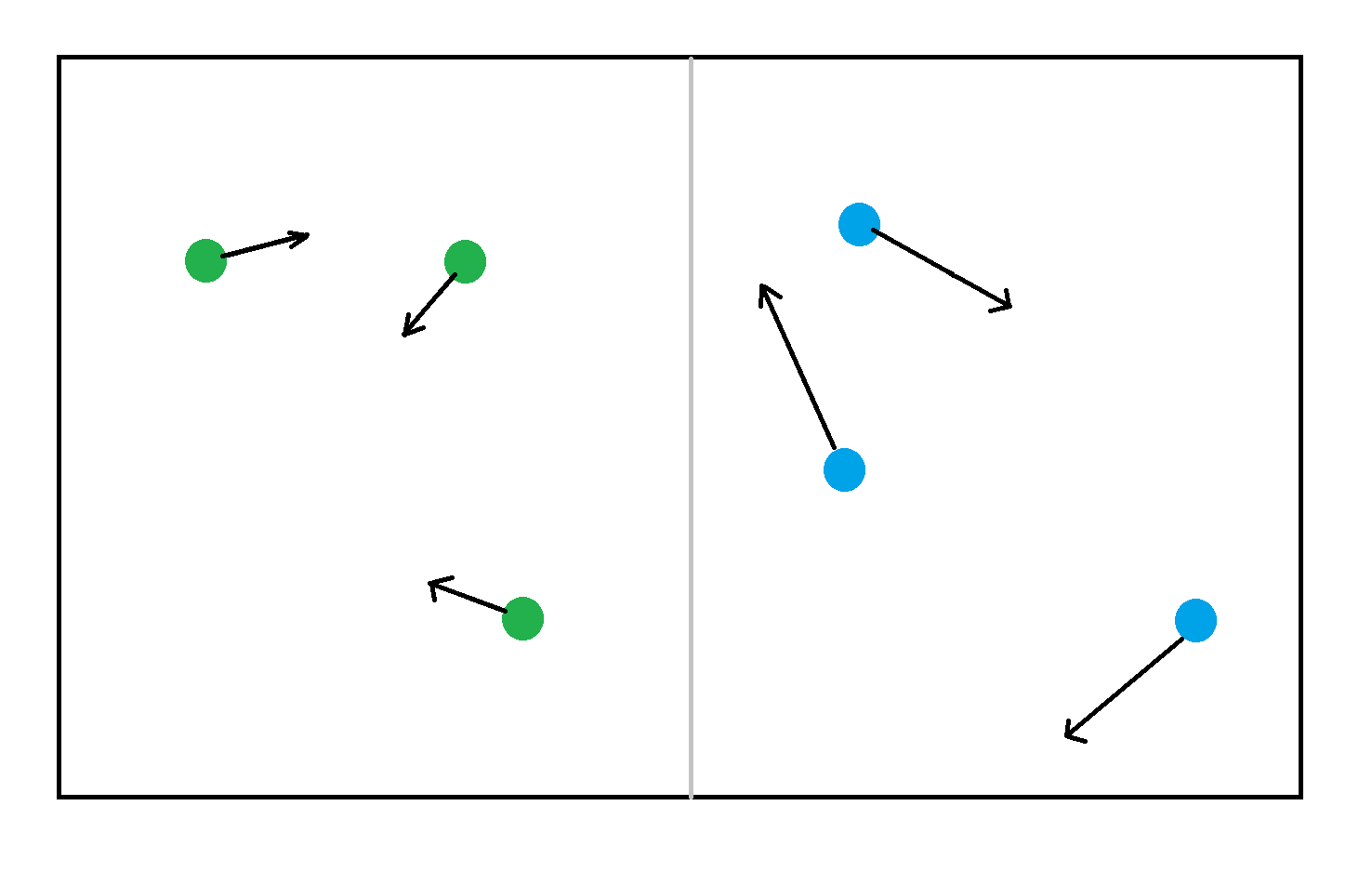
Consider two gasses, blue gas, and green gas, both gasses occupy the same volume, with the same number of particles, but the green gas particles are moving slower than the blue. The blue gas has more kinetic energy than the green gas.
Mathematical
$E_{therm} = N \frac{3}{2} k_{b} T= \frac{1}{2} N m V^{2}_{rms}$
$Nk_{b} = nR$
Thermal energy ($E_{therm}$}, Number of particles ($N$), Boltzman Constant ($k_{b}$), Temperature ($T$), Mass of particle ($m$), Velocity root mean square ($V_{rms}$), Number of mols ($n$), Rydberg constant ($R$).



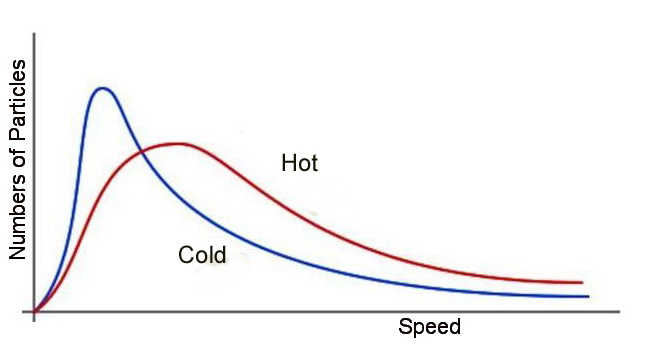
Graphical
The Maxwell distribution below describes the relationship between the probablity density and the velocity of particles relative to a temperature curve that informs us the range of velocities that the particles may have.
.
Descriptive
The thermal energy of the particles in a system is directly proportional to temperature, which applies to an ideal gas. As a consequence, the temperature of an ideal gas is also directly proportional to the average kinetic energy per atom.
Experimental
Since we know the temperature of an ideal gas is directly proportional to the average kinetic energy, we can design an experiment to lower the temperature of a gas and physically see the average kinetic energy of the gas molecules decrease. In the following video, air filled balloons are lowered into liquid nitrogen, which significantly lowers the temperature of the air inside the balloons. Therefore, as the kinetic energy of the gas molecules decreases, there are less and less air molecules colliding with the walls of the balloon and the balloon will shrink back to its original size.