Check out the equipotential surfaces of a bunch of charges dancing around each other.
Pre-lecture Study Resources
Watch the pre-lecture videos and read through the OpenStax text before doing the pre-lecture homework or attending class.
BoxSand Introduction
Electric Potential | Charges in a Field and the Total Energy of a System of Charges
Positive charges feel a force and speed up in the direction of decreased electric potential.
It's because that decreases the electric potential energy. All particles feel a force in the direction of decreased potential energy, but be careful, for a negative charge, it feels a force toward increased electric potential because that actually decreases the electric potential energy. The minus sign on the charge accounts for the difference between the positive charge moving towards decreased potential while the negative charge moves towards increased potential. Both do so to decrease the potential energy.
This example also illustrates the power of the field concept. Once we have found the electric potential field from a charge distribution, we can perform an infinite number of theoretical experiments on how much energy is converted between kinetic and potential for of any charge moving between locations in space. To make it more tangible, lets connect to the analogy of the gravitational field and gravitational potential energy. Recall that gravitational potential energy $U^g = mgh$. The gravitational field is equal to $gh$ and when multiplied by the mass you get the gravitational potential energy $mgh$. Since $g$ is a constant, the field really only depends on your height (or elevation). A topographical map is essentially a gravitational potential map.
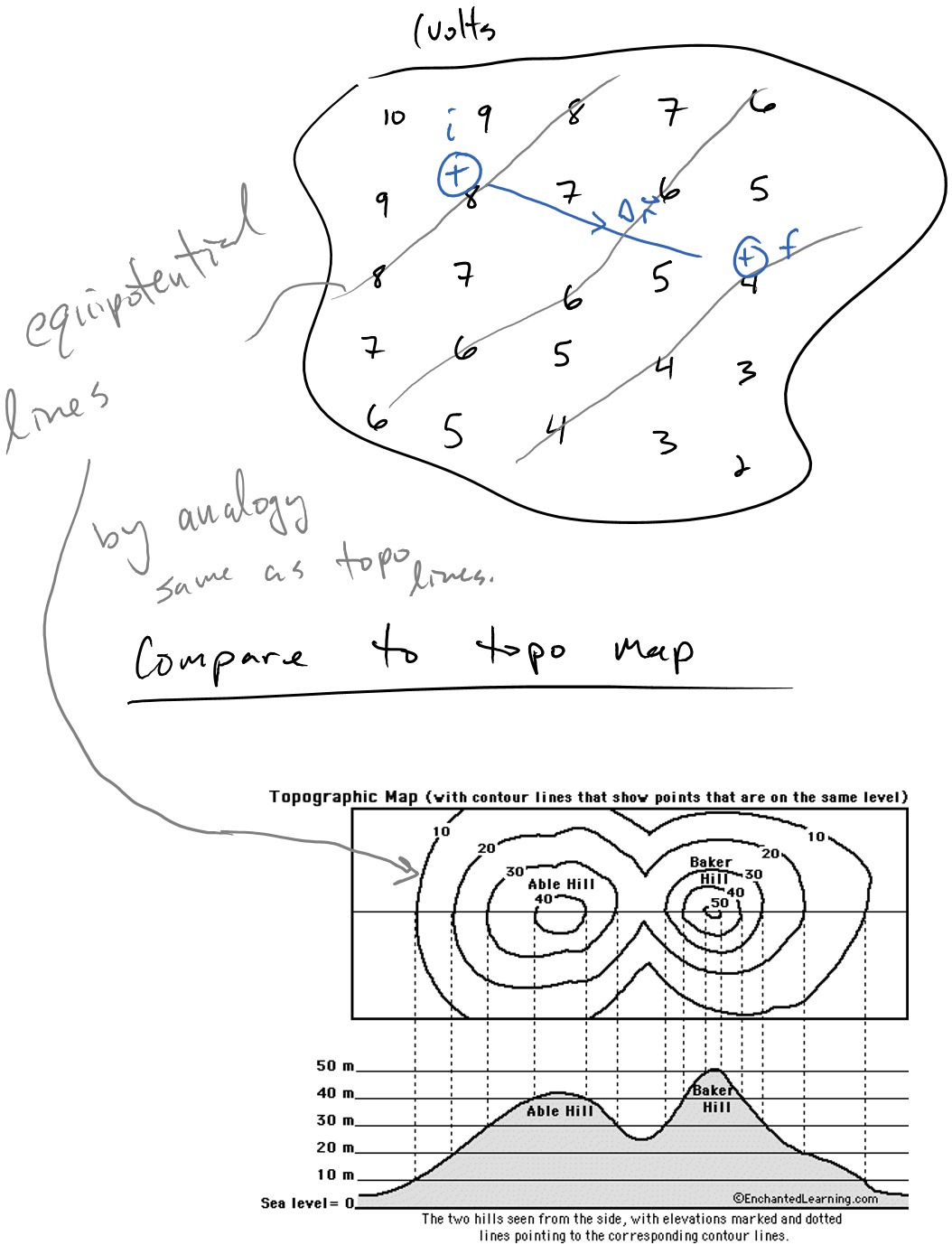
Lines (or really surfaces) called equipotentials can be used to describe places that have a constant potential and thus energy. Masses feel a force that make them want to move down the equipotentials, analogous to the positive charge above feeling a force towards decreased electric potential. In both cases (charges and masses) the systems move towards decreased potential energy. This is one of the most fundamental statements that can be made in physics - systems drive towards decreased potential energy. This is why water runs downhill.
Total Potential Energy of a Collection of Particles
One question that often arises is what is the total electric potential energy of a collection of particles. Imagine a single positive charge fixed in space. To bring a second charge close to the first, you'd have to do work to overcome the repelling force. If you did overcome that work and brought them next to each other, if they were released, they would fly away with kinetic energy. That kinetic energy comes originally from the work of bringing them together, which is converted into potential energy when they are close together. That potential energy can be thought of as the energy of the system. If you where to bring in more charges, you'd have to figure out the potential energy of all the combinations particles. The total potential energy for a system of three particles is described below.
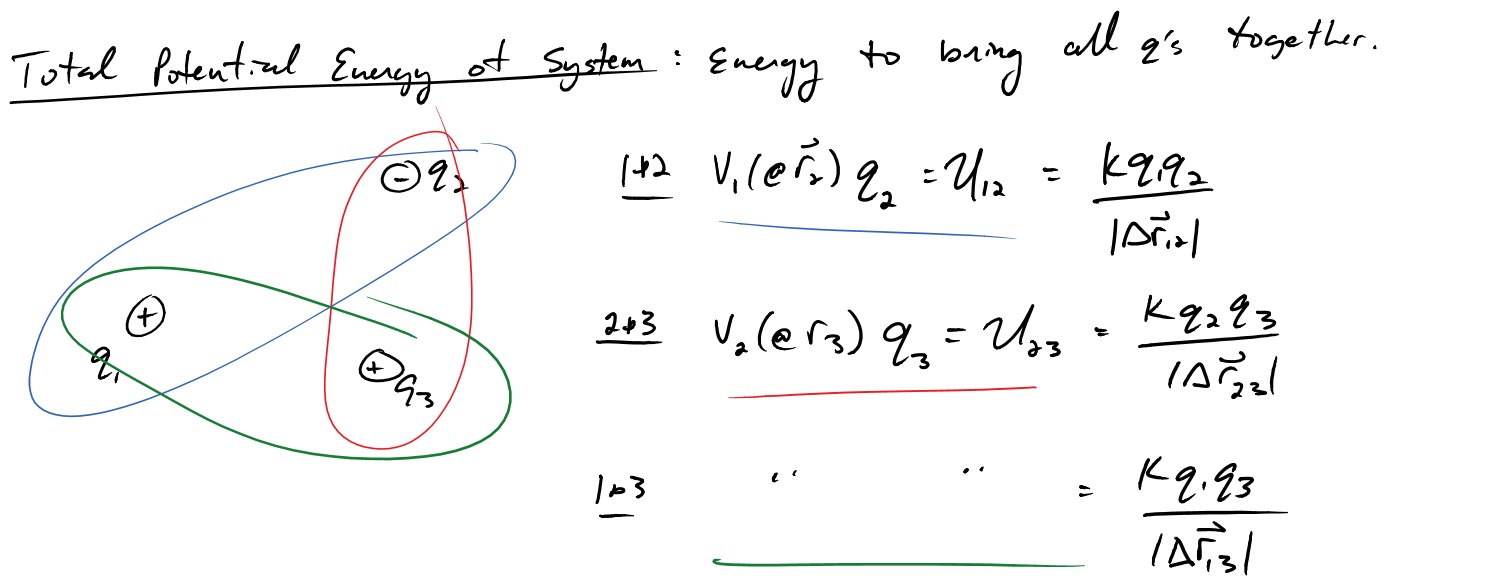
The total potential energy of the system of three particles is just summation of all the combinations. *Warning* don't over count interactions, $U_{12}$ is the total energy of the 1 and 2 system, meaning if you were to also include $U_{21}$, you'd be double counting. So it's only the unique pairs and the ordering of the subscripts does not matter.
$U_{total}=U_{12} + U_{23} +U_{13}$ ... + all combinations if there are more particles
This is how much energy would be released into kinetic energy if the system was released from rest. Notice that if there were negative charges present you could have a negative total potential energy. Systems with a negative potential energy are said to be bound systems as the particles have a net attraction to one another. They want to clump together as opposed to fly apart.
Key Equations and Infographics
Now, take a look at the pre-lecture reading and videos below.
BoxSand Videos
Required Videos
E-potential energy of a system of charges(8min)
Suggested Supplemental Videos
OpenStax Reading
Fundamental examples
1. Two plates of metal with uniform charge distribution are held a distance d apart from each other as shown in the figure below. The metal plate on the left side is positively charged while the metal plate on the right is negatively charged.
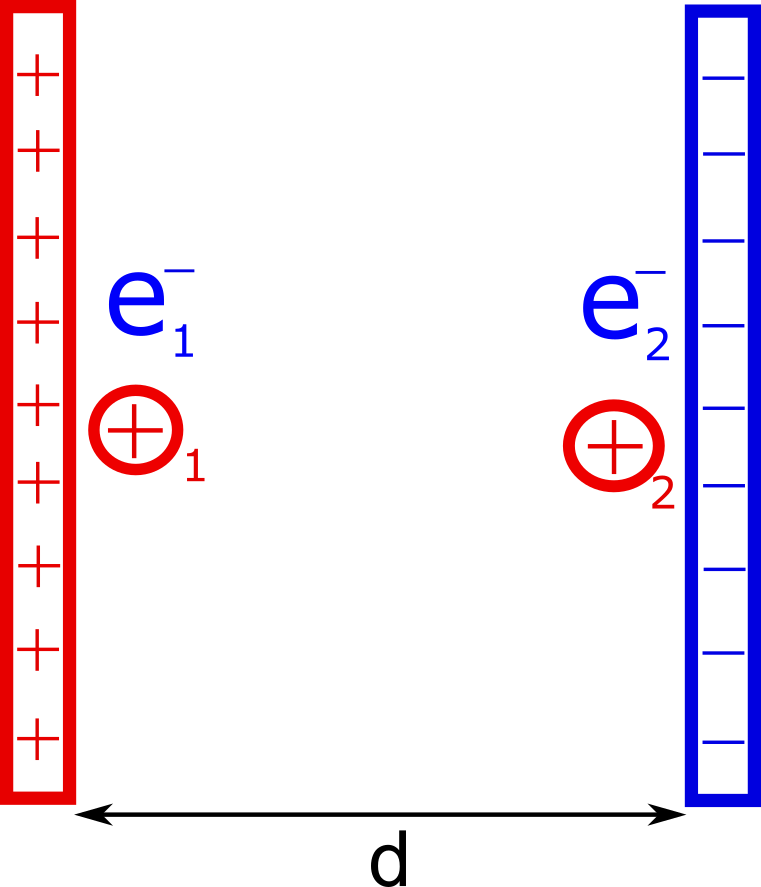
a. Which plate is considered to be at a higher potential ($V$)?
b. The electron labeled $1$ is placed in-between the two sheets as shown. Does this electron have a high or low electric potential energy? Ignore the other charges in-between the plates.
c. The electron labeled $2$ is placed in-between the two sheets as shown. Does this electron have a high or low electric potential energy? Ignore the other charges in-between the plates.
d. The proton labeled $1$ is placed in-between the two sheets as shown. Does this proton have a high or low electric potential energy? Ignore the other charges in-between the plates.
e. The proton labeled $2$ is placed in-between the two sheets as shown. Does this proton have a high or low electric potential energy? Ignore the other charges in-between the plates.
2. Two parallel plates are held $20.0 \, mm$ apart and the potential difference between the plates is $110 \, V$.
a. What is the magnitude of the electric field between the two parallel plates?
b. Which direction does the electric field point if the plate on the left has a uniform negative charge distribution and the plate on the right has a uniform positive charge distribution?
c. Sketch a physical representation of this problem. Include a few equipotential lines between the two parallel plates.
3. Two uniformly charged parallel plates are held some distance “$d$” apart from each other with an electric potential of $300 \, V$ between them. An electron is placed at rest near the negative charged plate. Calculate the speed at which the electron will hit the positive plate.
4. The figure below shows a charge distribution made up of $3$ point charges. The charges are fixed in space and cannot move. Let $q = 1 \, \mu C$ and $L = 1.0 \, cm$.
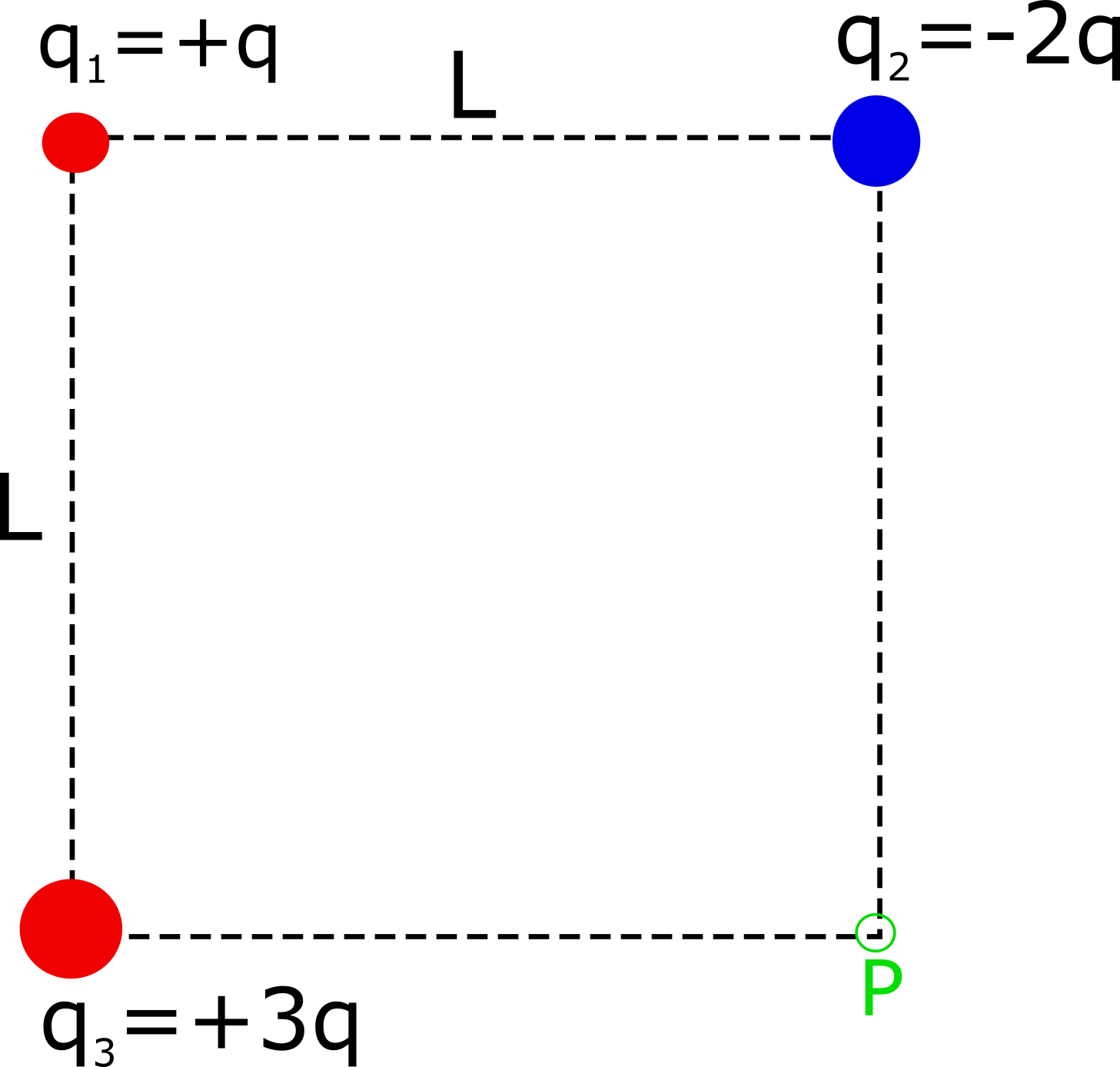
a. Find the electric potential energy of this charge distribution.
b. Find the electric potential at point P.
CLICK HERE for solutions.
Short foundation building questions, often used as clicker questions, can be found in the clicker questions repository for this subject.
Post-Lecture Study Resources
Use the supplemental resources below to support your post-lecture study.
Practice Problems
BoxSand practice problems - Answers
BoxSand's multiple select problems
BoxSand's quantitative problems
Recommended example practice problems
- OpenStax and it's 4 related sections. Problems at bottom of page,
- Electric Potential Energy, Website Link
- Electric Potential in a Uniform Electric Field, Website Link
- Electric Potential Due to a Point Charge, Website Link
- Equipotential Lines, Website Link
- Physics-Prep
- Electric Potential, Website Link
- Electric Potential Due to Point Charges, Website Link
- Equipotential Surfaces, Website Link
For additional practice problems and worked examples, visit the link below. If you've found example problems that you've used please help us out and submit them to the student contributed content section.
Additional Boxsand Study Resources
Additional BoxSand Study Resources
Learning Objectives
Summary
Summary
Atomistic Goals
Students will be able to...
YouTube Videos
Pre-Med Academy has a lot of videos about the Electric Field and Force, too many to list here. We really recommend checking out the content repository for this section and check out the rest of their videos Here are just a few on Work and Potential Energy, Electric Potential Difference, and Potential of a Point Charge
Youtube: Pre-Med Academy - Potential of a point charge
Step By Step Science has a bunch of practice problems having to do with electric potential and we suggest you check out your content repository for this section to see a list of relevant videos from them. Here are a few on work done moving a point charge through a potential difference, calculating potential difference between two points, and work to bring in a charge from infinity.
Other Resources
This link will take you to the repository of other content related resources .
Simulations
This flashphysics applet lets you create charge distributions from point charges and plot the corresponding equipotential lines. Try placing test charges in the region of space to watch possible trajectories!
This PhET interactive combines electric fields, electric potential and charge (known collectively as electrostatics). Place charges around and observe the resulting electric and potential fields.
For additional simulations on this subject, visit the simulations repository.
Demos
History
Oh no, we haven't been able to write up a history overview for this topic. If you'd like to contribute, contact the director of BoxSand, KC Walsh (walshke@oregonstate.edu).
Physics Fun
Other Resources
Resource Repository
The Physics Classroom has two sections for us, one on electric potential and the other on electric potential difference.
| Electric Potential | Electric Potential Difference |
Boston University's Page on electric potential is a neat reference with a couple of example problems
PPLATO is a complete resource with a lot of information, and several practice questions per subject. This webpage covers electric charge, the electric field, and electric potential, we've already covered charge, and the electric field, so now it's time to focus on electric potential!
Isaac Physics' section on the electric field is a good short resource. This page contains previously studied material on electric fields as well as information on electric potential, and the connection between electric field and electric potential.
Other Resources
This link will take you to the repository of other content related resources .
This link will take you to the repository of other content related resources.
Problem Solving Guide
Use the Tips and Tricks below to support your post-lecture study.
Assumptions
Checklist
Misconceptions & Mistakes
- The electric potential from a point charge is proportional to $\frac{1}{r}$, not $\frac{1}{r^2}$.
Pro Tips
Multiple Representations
Multiple Representations is the concept that a physical phenomena can be expressed in different ways.
Physical
Mathematical
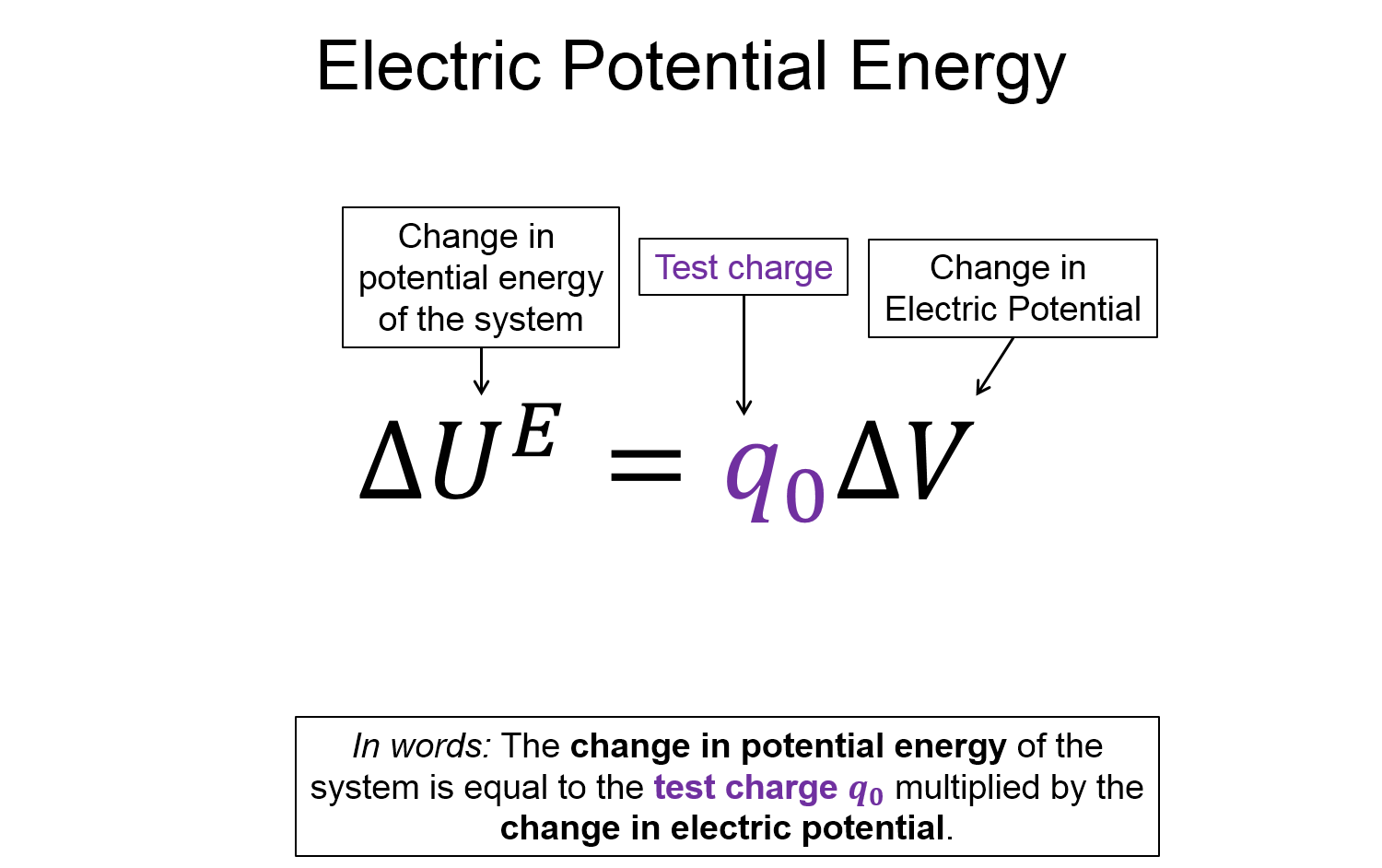
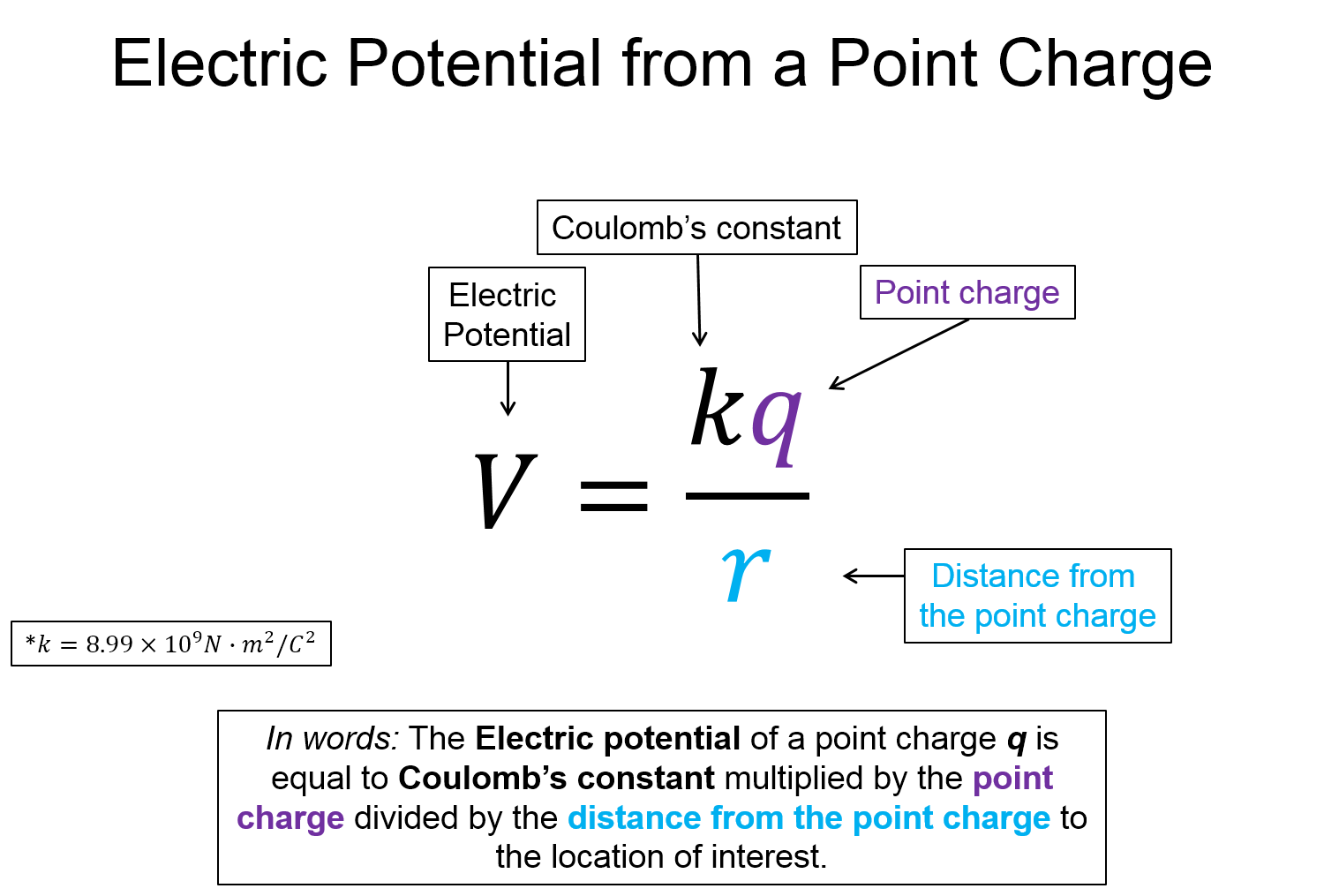


Graphical
Descriptive
Experimental