A vector is a mathematical object with both direction and magnitude. Vectors are visualized by an arrow, where the arrow's point represents the direction and its length represents the magnitude. Vectors can be added to other vectors and multiplied (or scaled) by numbers, known as scalars.
Why use these mathematical objects, and how might you have seen them before? Any time you give someone directions you are describing a vector, ie, "go southeast (direction) 50 steps (magnitude)". In physics, you will see vectors used to describe motion, gravity, electricity, magnitism, and much more.
Now, check out Vector's description of a vector (from Despicable Me).
Pre-lecture Study Resources
Read the BoxSand Introduction and watch the pre-lecture videos before doing the pre-lecture homework or attending class. If you have time, or would like more preparation, please read the OpenStax textbook and/or try the fundamental examples provided below.
BoxSand Introduction
Review and Vectors | Vector Operations
Vectors can be used to represent anything that has a direction and magnitude, such as velocity, acceleration, forces, displacement, or electric and magnetic fields.
Scalars are just a number, and can represent speed (magnitude of velocity), time, temperature, and distance (magnitude of displacement.
Here are some ways to represent vectors:
Cartesian (component): $\overrightarrow{A} = \langle A_x, A_y, A_z \rangle$
Image of cartesian
Polar: magnitude and (angular) direction $(|\overrightarrow{A}|,\theta)$
We have focused so much on creating introductions to the physics content we haven't had time to create text that reviews vectors. We do however have good videos on what you'll need to know starting this class. Check them out below in the drop down called BoxSand Videos. You can also check out the vectors sections of the OpenStax Textbook in the drop down below.
BoxSand Videos
Required Videos
Suggested Supplemental Videos
OpenStax Reading
Section 3.2 of the OpenStax text book provides additional understanding of graphical methods of vector operations.
Section 3.3 of the OpenStax text book covers analytical methods of vector component decomposition and vector operations like addition and subtraction.
Post-Lecture Study Resources
Use the supplemental resources below to support your post-lecture study.
Practice Problems
Check out the step by step Vector Review Worksheet below. There are questions intermixed with the review material. Try and work the problems before checking out the solutions.
Vector Review Worksheet ======> Click HERE
Vector Review Solutions ======> Click HERE *** NOTE: question 1 has some missing minus signs ***
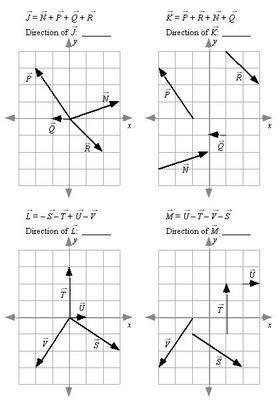
MR-VEC-1 Which of the following vector equations correctly describes the relationship among the vectors shown in the figure?
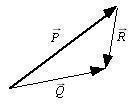
1. P + Q = R
2. P = Q + R
3. P + R = Q
4. P + Q + R =0
5. None of equations A - D is correct
MR-VEC-2 Start at the corner of a cube, of side length 1 m, and find the distance to the furthest point that still resides on the cube.
Note: the magnitude of a vector in three dimensions is the square root of the summation of the square of all three components of the vector.
Note: your answer should include units.
MR-VEC-3 You take off from La Guardia airport in a little airplane. First you fly NW for 5 miles. At the George Washington bridge, you turn SSW for 10 miles. Above the Statue of Liberty, you turn S toward the Verazzano Narrows bridge, 5 miles ahead. Over the bridge you turn ENE for a landing at JFK airport, 10 miles ahead.
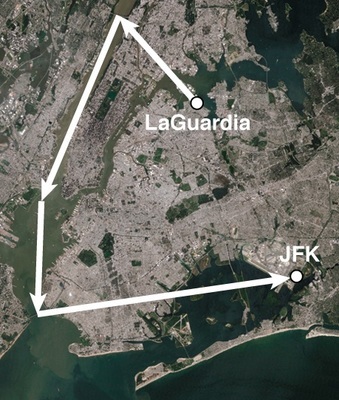
Suppose that instead of flying NW-SSW-S-ENE, you had followed the same "vectors" in a different sequence: SSW-NW-ENE-S. Mark on the map where this path would have led you.
MR-VEC-4 Three vectors, labeled P, Q, and R, are shown. The length of each vector is given in arbitrary units.
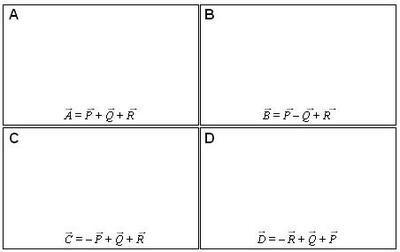
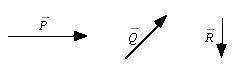
In each space provided above, construct a drawing of the indicated combinations of the vectors P, Q, and R, and then rank the magnitude of these resultant vectors.
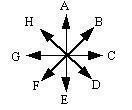
MR-VEC-5 For each situation below, combine the vectors as indicated and determine the direction of the resultant vector. Then select the closest direction to the resultant from the direction rosette.
*** The questions from here down involve applying vector operations to positition, velocity, and acceleration ***
MR-VEC-6a Estimate the position vector to the location in the room defined as point A. Set the origin at the front, bottom, right side of the room (as seen by the students). Consider left to right as the positive x direction, bottom to top as positive y direction, and front to back as the positive z direction.
Answer in whole numbers of meters with the following format: <x,y,z> m. An example might look like: <4,1,7> m.
Estimate the position vector to the location in the room defined as point B.
Using the class average for position vectors A and B, find the displacement vector from point A to B. Answer in whole numbers of meters with the following format: <Δx,Δy,Δz>. An example might look like: <4,1,7> m.
MR-VEC-6b New Origin
Estimate the position vector to the locations in the room defined as point A and point B.
This time set the origin at the front, top, left side of the room (as seen by the students). Consider left to right as the positive x direction, bottom to top as positive y direction, and front to back as the positive z direction.
Answer in whole numbers of meters with the following format: <xA,yA,zA> m, <xB,yB,zB> m. An example might look like: <4,1,7> m, <-2,3,6> m.
Using the class average for position vectors A and B from the new origin, find the displacement vector from point A to B.
Answer in whole numbers of meters with the following format: <Δx,Δy,Δz>. An example might look like: <4,1,7> m.
MR-VEC-7 Deserted on a deserted Island you spot a slightly exposed tin can under a tree. Upon opening it you find instructions to a buried treasure. It reads: “Ten paces from this very tree in a direction twenty degrees south of west lies the first location. Ten paces from this very tree in a direction sixty degrees north of east lies the second location. Walk from this tree exactly the distance and direction you would walk from the first location to the second location and you will find ye treasure. Yar” Sketch a physical representation of this situation on the grid provided. A physical representation for this type of problem should include the two position vectors, the change in the position vector, and the location of the treasure. Use the center of the grid as the tree location and scale appropriately to fit on the grid.
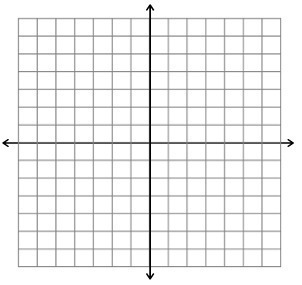
What are the coordinates of treasure?
MR-VEC-8 Upon waking from being hit in the head with a shovel you find yourself in the woods, next to a unfilled grave. You start running from this nightmare in a direction 51.34 degree from the negative y direction towards the negative x direction. Your acute direction senses surprise you but this is no time to contemplate a new super-power. You run along that line for 6.403 miles until you run into a police officer located at a location <-2, -3> miles from the police station. What are the coordinates of the grave you were presumably destined for?
1. <1, 8> mi
2. <4, -5> mi
3. <-2, 3> mi
4. <-1, -1> mi
5. <3, 1> mi
Additional Boxsand Study Resources
Additional BoxSand Study Resources
Learning Objectives
Summary
The objective is to introduce vector mathematics in multiple representations through the use of physical quantities such as position, displacement, average velocity, and average acceleration.
Atomistic Goals
Students will be able to...
- Identify if a physical quantity is a vector or a scalar.
- Describe a vector using the descriptive, physical, and mathematical representation.
- Convert between polar (magnitude and direction) and Cartesian coordinates (x & y).
- Represent vectors using many standard notational representations, e.g. $\langle x, y \rangle$; $\hat{x} + \hat{y}$; and $\hat{i} + \hat{j}$.
- Translate between the descriptive and physical representations of a vector.
- Translate between the physical and mathematical representations of vector.
- Multiply a vector by a scalar in the mathematical and physical representations.
- Add vectors using the physical representation with the head-to-tail method or parallelogram method when tail-to-tail.
- Add vectors using the mathematical representation.
- Subtract vectors with the tools of vector addition.
- Subtract vectors using the physical representation with the tail-to-tail method.
- Subtract vectors using the mathematical representation.
- Determine the summation (net) of a set of more than two vectors.
- Manipulate vector equations using the rules of algebra.
- (UPMF) Select between using vector algebra and geometrical methods when finding distances.
- Recognize that multiplication and division of two vectors are not possible operations - advanced operations of dot and cross products will be presented when the physical situation warrants it.
YouTube Videos
Here are some Khan Academy on vector operations, namely scalar multiplication and addition of vectors.
Here is an example of adding and subtracting vectors.
Simulations
1. Check out the PhET simulation that helps you visualize adding vectors.
For additional simulations on this subject, visit the simulations repository.
Demos
History
Oh no, we haven't been able to write up a history overview for this topic. If you'd like to contribute, contact the director of BoxSand, KC Walsh (walshke@oregonstate.edu).
Physics Fun
Other Resources
Check out the Physics Classroom's quick intro to Vectors vs. Scalars. Take the Check your Understanding quiz!
Resource Repository
This link will take you to the repository of other content on this topic.
Problem Solving Guide
Use the Tips and Tricks below to support your post-lecture study.
Assumptions
- Vectors always have 2 things: Magnitude and direction or x and y components. Never write out a vector quantity (position, velocity, acceleration, etc.) without BOTH elements of the vector present.
- All vectors corresponding to the same quantity can be added tip-to-tail (one leading into the other) to get a single resultant vector corresponding to both added together.
- Vectors with negative signs in front means they have flipped direction.
- A scaler (just a number, with or without units, or magnitude) multiplied onto a vector alters its length (or changes it to the opposite direction if it is negative).
Checklist
1. Read and re-read the whole problem carefully.
2. Visualize the scenario. Mentally try to understand what the object is doing.
a. Motion or vector diagrams are a great tool here for visual cues as to what the motion of an object looks like.
3. Draw a physical representation of the scenario; include any vectors or length values and note the scaler values (like time) to the side of the diagram.
4. Define a coordinate system; place the origin on the physical representation where you want the zero location of the x and y components of position.
5. Identify and write down the knowns and unknowns.
6. Write out the mathematical representation for the physical representation you drew in step (3).
7. Carry out the algebraic process of solving the equation(s).
a. If simple, desired unknown can be directly solved for.
b. May have to solve for intermediate unknown to solve for desired known.
c. May have to solve multiple equations and multiple unknowns.
d. May have to refer to the geometry to create another equation.
8. Evaluate your answer, make sure units are correct and the results are within reason.
Misconceptions & Mistakes
- Differentiate between scaler and vector quantites, the difference is the addition of directional information in vectors.
- When adding vectors, components of two adding vectors can cancel out if they are in opposite directions.
- Constants (such as g) never contain inharent directional information, they are scalers, meaning they are or are part of the magnitude.
- Learn to work with visual representations of vectors as well as mathematical ones. When you make an error doing one way, and can usually catch it with the other.
Pro Tips
- Always ask yourself if the questions is asking for a vector or a scalar quantity.
- Always ask yourself it the information given is a vector or scalar quantity.
- Always ask if your units work after you have done some manipulation of an equation, this simple trick can catch most errors in algebra.
- Draw a physical representation for the situation. Often this includes vector operation diagram.
- Always think about your coordinate system and which way your defining as positive and negative, the choice is arbitrary unless given in a problem, but you MUST be consistant in your description of all vector quantities in reference to that coordinate system throughout the problem.
- Ask if your answer makes sense in the end. Does the number seem reasonable? If it is a vector, is it pointing in the direction you would predict it would? Is the sign right? Do the units in your equation work? These are always great questions to ask, but use them as your first line of defense if you don't get the right answer or something feels off.
Multiple Representations
Multiple Representations is the concept that a physical phenomena can be expressed in different ways.
Physical
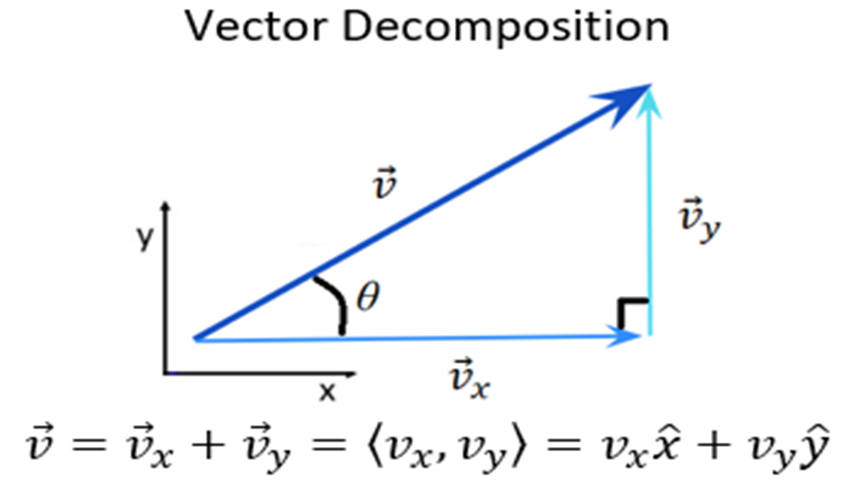
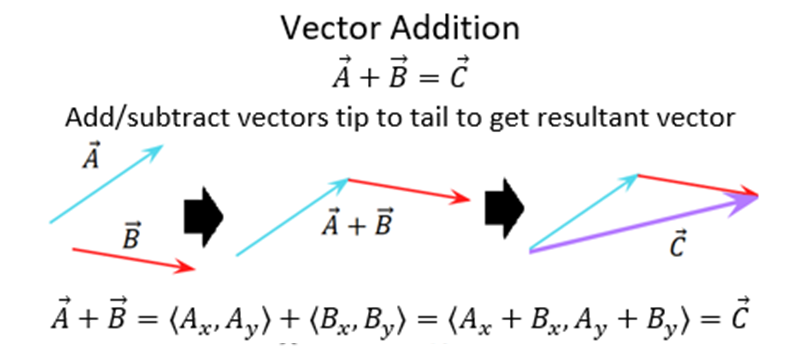
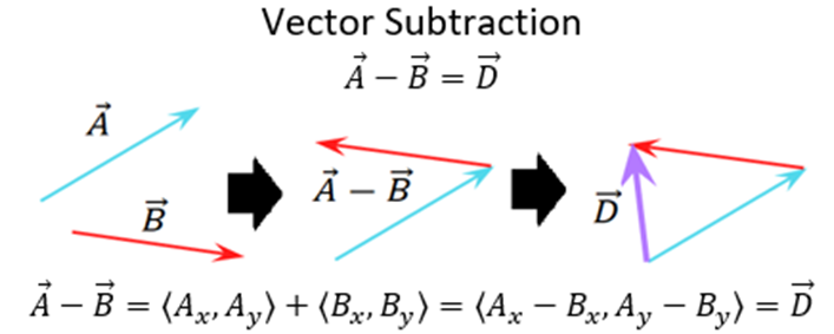
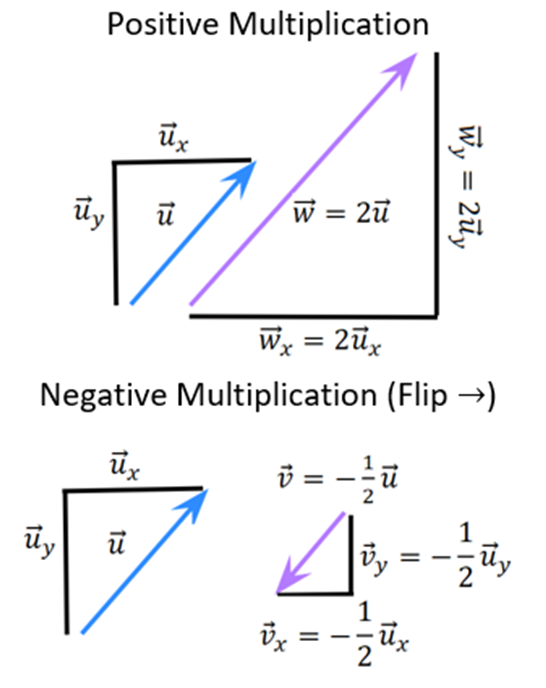
Mathematical

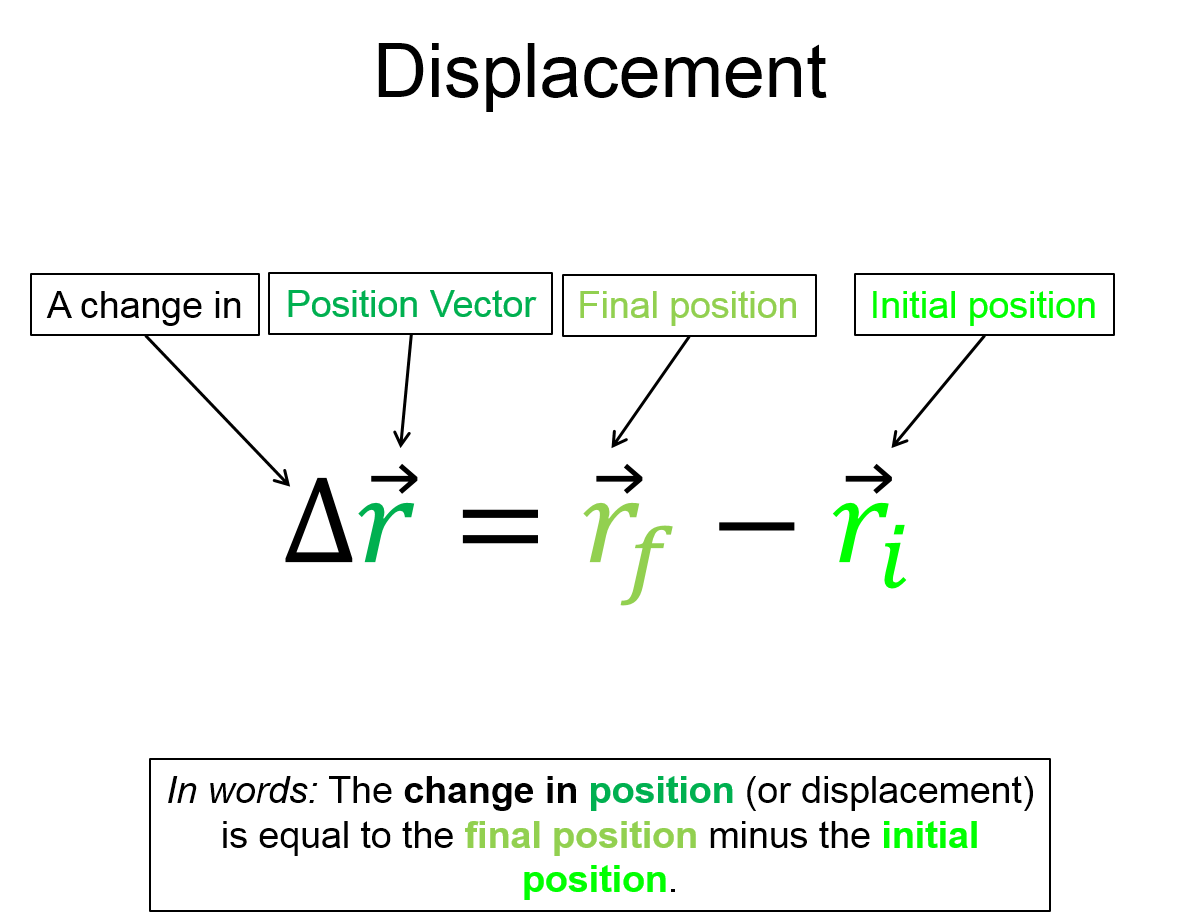
Graphical
Below is a graph with position on the vertical axis and time on the horizontal. The curve shows a tangent line, or slope, representing in instantaneous velocity at one point. There is also a representation of the average slope and thus velocity between two points.

Descriptive
Experimental
We could go out to an ordinary city block and time how long it takes to walk from one corner of the block to the exact opposite corner. In this way, we could walk around the outside of the block and measure the distance traveled on foot around the block. Each side of the block would represent a position vector. From the mathematical representation section we would certainly know what to do with the rest information. Therefore, we can easily calculate the the average velocity.