Smarter Every Day explains the workings of a perfect example of a thermodynamics system, an engine.
Pre-lecture Study Resources
Watch the pre-lecture videos and read through the OpenStax text before doing the pre-lecture homework or attending class.
BoxSand Introduction
Thermo | Ideal Gas Cycles and Efficiency
Thermodynamic cycles of gases are used everywhere in modern society to do our bidding. From diesel engines to refrigerators, we use expansions and contractions of gases, along with work and heat exchanges and the 1st law, to solve problems with thermodynamic machines. What is also nice about studying thermo cycles is that they are an ideal place to put almost all the thermo we have learned into one problem.
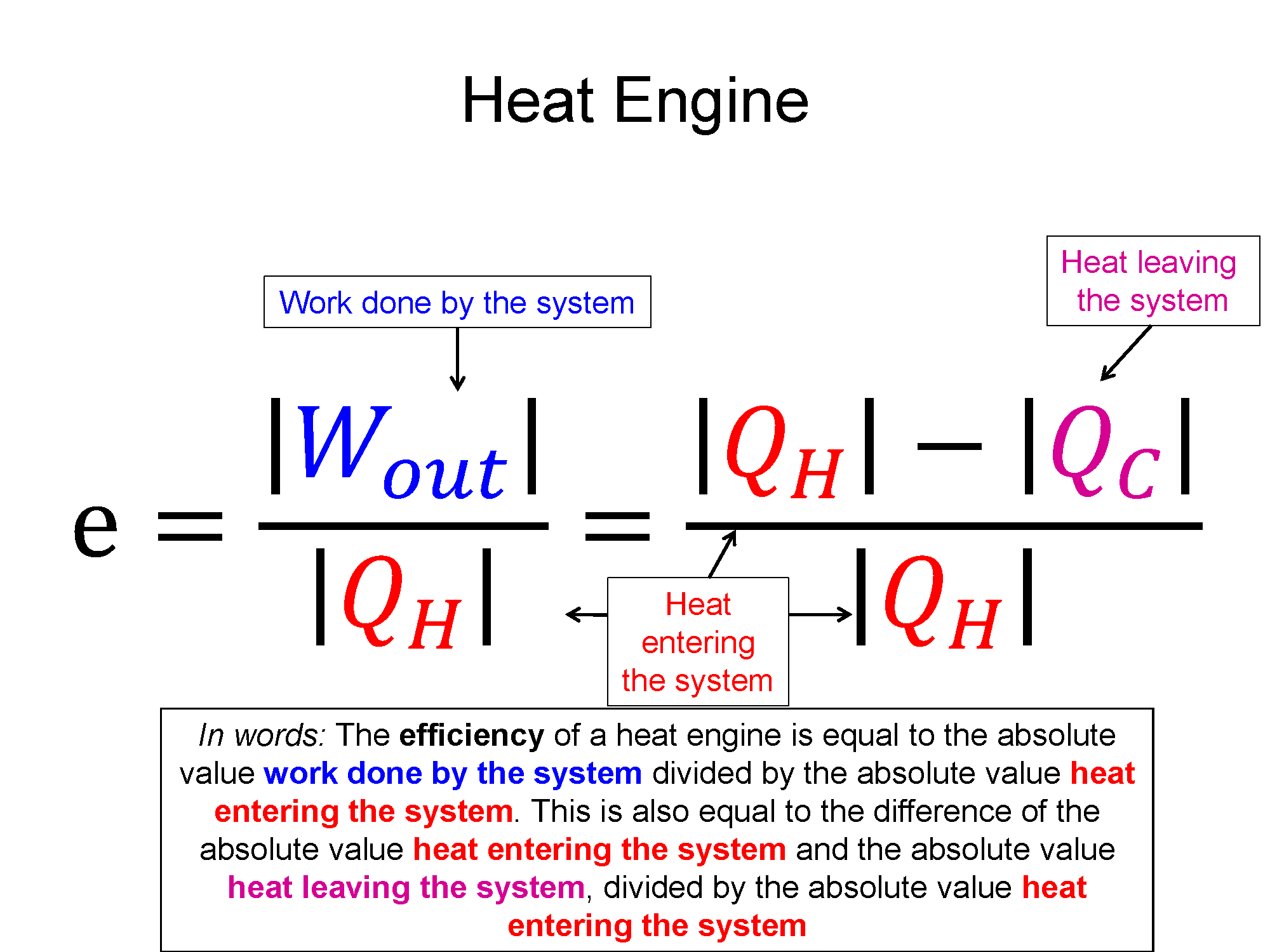
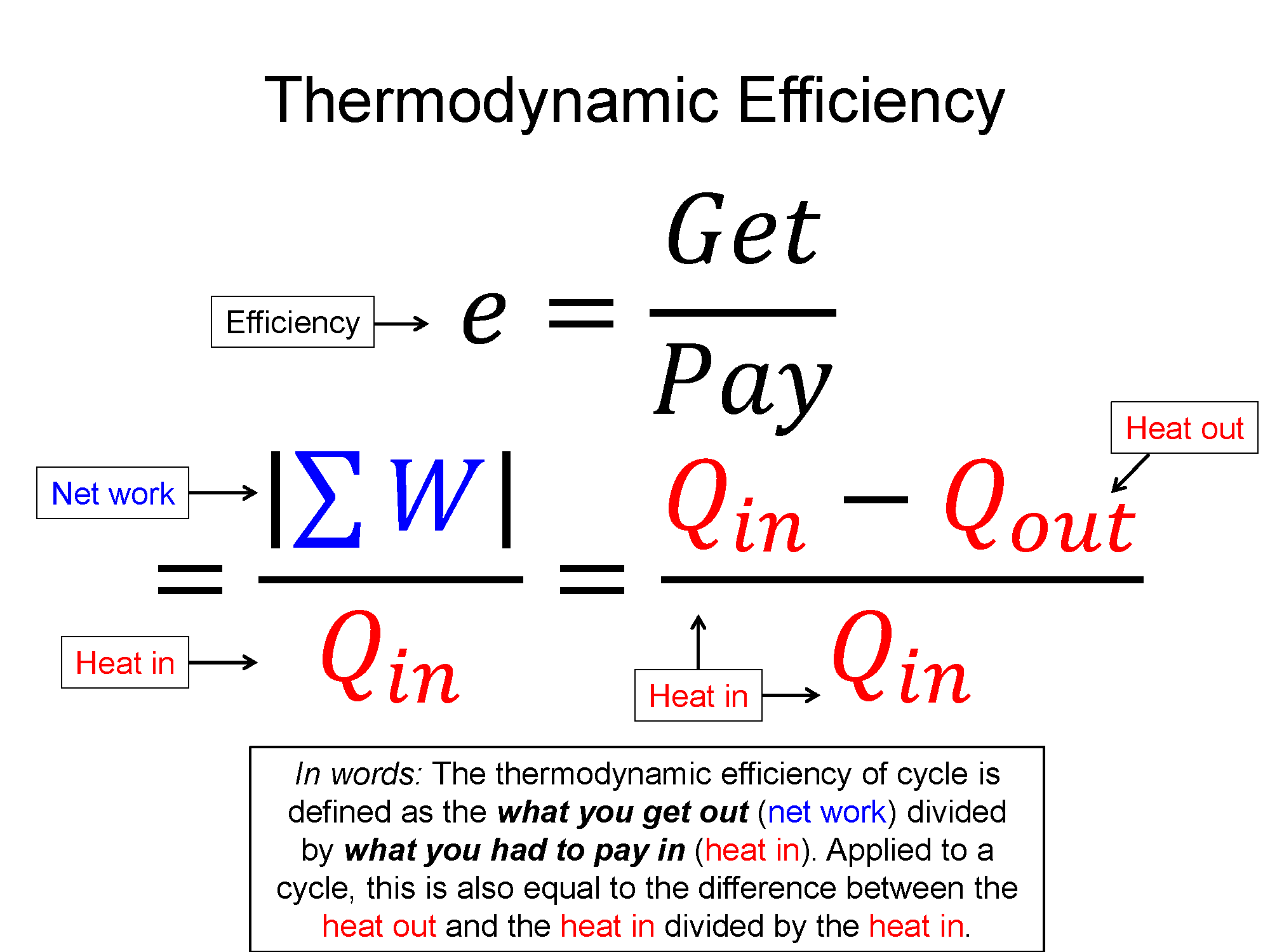
One type of cyclical process is a heat engine, sometimes called a power cycle. These are cycles where there is a net work out of the system, a steam engine being an example. One of important quantities in this case is the thermodynamic efficiency. In the example of the steam engine, you take stored chemical potential energy in the coal/wood and using a thermodynamic process of heat transfer (burning) you are able to get useful work out (train starts moving). The thermodynamic efficiency of cycle is defined as the what you get out (net work) divided by what you had to pay in (heat in).
$e = \frac{what-you-get-out}{what-you-pay-in}=\frac{|\sum W|}{\sum Q_{in}}$, where $Q_{in}$ is all the positive Q's
using the 1st law $\Delta E_{th}=Q+W$, the efficiency can also be written as $e=\frac{Q_{in} - Q_{out}}{Q_{in}}$
An example of a heat engine is shown in the PV-diagram below. Since there is more work done on the expansion stage (B=>C) of the cycle then the compression (D=>A), this has a net work out.

If the cycle was able to be run in reverse, there would be a net work into the system and it would be considered a refrigeration cycle. In those cases, efficiency is not used to describe the process but rather something called the coefficient of performance. We have chosen to focus on heat engines and not refrigeration cycles here. What you should also note about the above diagram is that after one complete cycle, A to B, B to C ... and back to A, the system is back to its original state. That means that after one complete cycle the change in temperature is equal to zero. If that was not the case and each cycle the temperature increased or decreased, the system would not be in steady state and would continue to change its temperature until it melted or froze. With $\Delta T$ equal to zero, the total $\Delta E_{th}$ must also be zero. For a cycle the overall change in thermal energy is zero but the overall net work and heat are not.
One way to visualize a heat engine is to use a Sankey diagram where arrows represent the energy transfers.
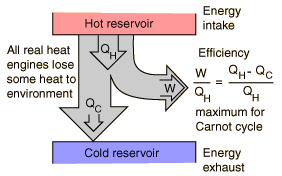
All heat engines ultimately operate between a hot and cold reservoir. As heat flows from the hot to the cold reservoir, useful work is extracted. Some energy though always has to be exhausted to the cold temperature reservoir, entropy is the driver of this feature. The 2nd law of thermo drives this process and forces there to never be a perfectly efficient process - heat cannot be 100% converted into work. One way to accept this fact is to imagine the diagram above flowing all the heat from the hot reservoir out to work. If that was the case the system would no longer be in contact with the cold temp reservoir and then what would be driving the heat transfer?
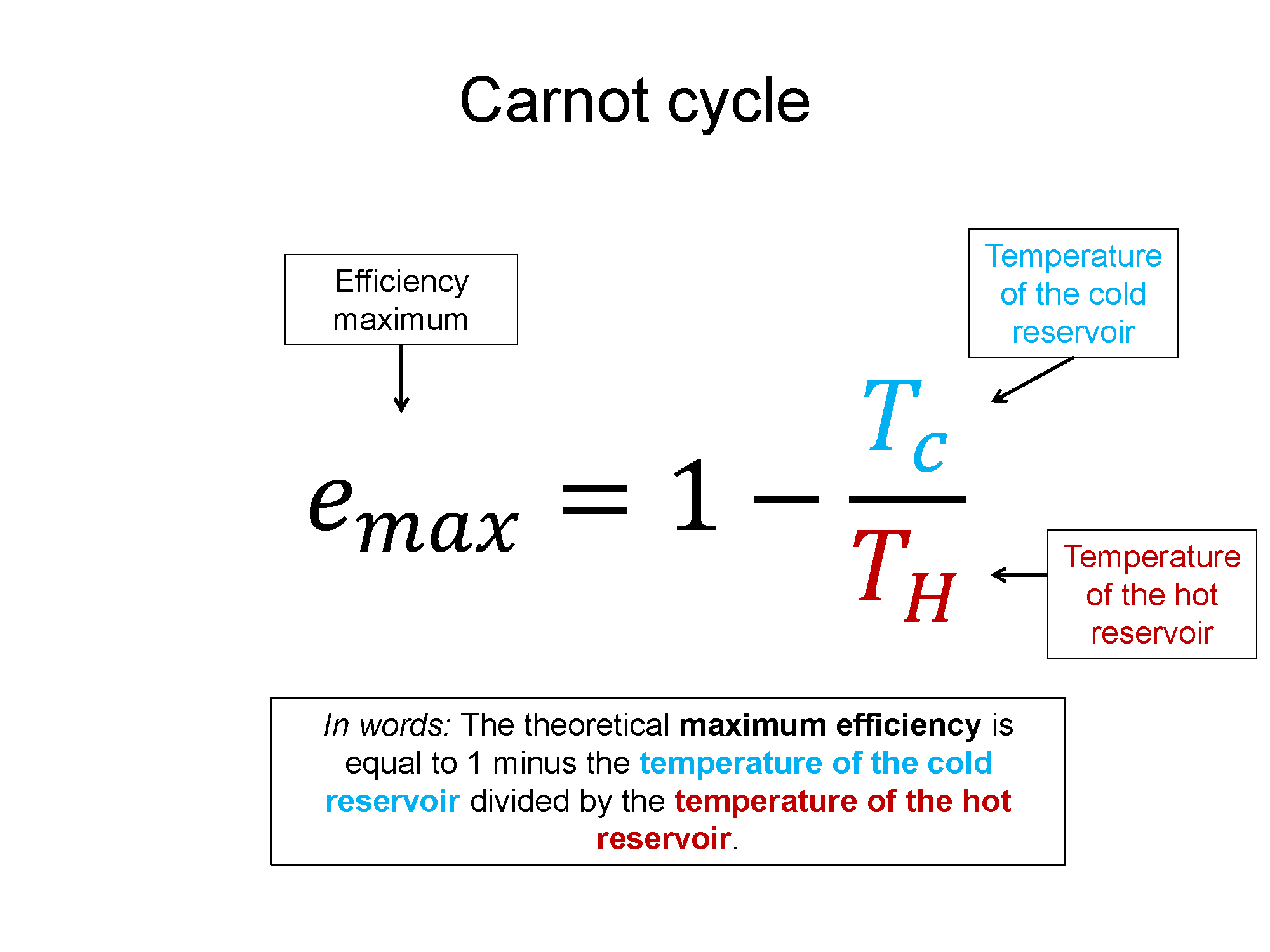
There is such a thing as a theoretically maximum efficient cycle. That cycle is called a Carnot cycle and the max efficiency can be written in terms of the temperature of the hot and cold reservoirs.
$e_{max} = 1-\frac{T_C}{T_H}$
Thermodynamic cycles often involve what I like to call a murder mystery exercise. You are given some of the state variables and/or some of the energy transfers for a complete cycle. Then you have use the first law of thermo, the ideal gas law, and sometimes even the kinetic theory of gases to find the rest of the quantities. Drawing PV-diagrams and making tables are useful tools in these exercises.
Key Equations and Infographics
BoxSand Videos
Required Videos
Suggested Supplemental Videos
OpenStax Reading
OpenStax Section: none
Openstax has three sections relevant to thermodynamic cycles.
| Second Law and Heat Engines | The Carnot Heat Engine | Heat Pumps and Refrigerators |
Fundamental examples
Short foundation building questions, often used as clicker questions, can be found in the clicker questions repository for this subject.
Post-Lecture Study Resources
Use the supplemental resources below to support your post-lecture study.
Practice Problems
BoxSand's quantitative problems
Recommended example practice problems
- There are three sections from the openstax textbook which all have large sets of practice problems related to thermodynamic cycles. The practice exercises are located at the bottom of the pages.
- 15.3 Second Law and Heat Engines, Website Link
- 15.4 The Carnot Heat Engine Website Link
- 15.5 Heat Pumps and Refridgerators Website Link
For additional practice problems and worked examples, visit the link below. If you've found example problems that you've used please help us out and submit them to the student contributed content section.
Additional Boxsand Study Resources
Additional BoxSand Study Resources
Learning Objectives
Summary
Summary
Atomistic Goals
Students will be able to...
YouTube Videos
Heat Engines explained
Other Resources
This link will take you to the repository of other content related resources .
Simulations
This simulation allows you to explore a thermodynamic cycle with a PV Diagram. You can move any/all the points or sides of the cycle and see the impact on the Work, Energy, and Energy:
For additional simulations on this subject, visit the simulations repository.
Demos
A 4-stroke engine is a perfect example of using a thermodynamics cycle to get useful work.
For additional demos involving this subject, visit the demo repository
History
Oh no, we haven't been able to write up a history overview for this topic. If you'd like to contribute, contact the director of BoxSand, KC Walsh (walshke@oregonstate.edu).
Physics Fun
Other Resources
Here is a HyperPhysics page talking about PV-Diagrams and their ability to explore/explain engines:
Boston University's page on thermodynamic cycles,
Resource Repository
This link will take you to the repository of other content related resources.
Problem Solving Guide
Use the Tips and Tricks below to support your post-lecture study.
Assumptions
Checklist
Begin filling in the table with "non-calculation" values - values you can read right off the plot.
Use proportional reasoning to find the Tempearture at the points in the cycle.
If actual numbers are given in the problem, calculate the numerical value of P, V, and T at the points on the cycle.
Make a First Law table.
Fill in zeroes during steps where there is no work - whenever $V$ is constant.
Calculate $\Delta E$ for each step by using the equipartition theorem $\Delta E = D\frac{1}{2}Nk_b \Delta T$ where D is the degrees of freedom for your substance - $D=3$ for a monatomic gas.
Use the First Law $\Delta E = Q + W$ to solve for the heat.
Recall that $ PV = nRT = Nk_B T$, so if you have the equipartition theorem that says $\frac{3}{2} Nk_B \Delta T = \Delta E$, you can relate that to $PV$, which makes adding up totals easier. Do not report Q totals as ex $3NRT - PV$, convert to the same state variables.
Fill in remaining spots on table and sum up totals.
*GOOD way to check your work: Make sure that total $\Delta E=0$.
Misconceptions & Mistakes
Pro Tips
Multiple Representations
Multiple Representations is the concept that a physical phenomena can be expressed in different ways.
Physical
The diagrams below describe the heat engine process.The heat engine, or system takes in energy from a hot source where the heat energy is extracted to do work and waste leaves the system as used energy to the cold resevoir.
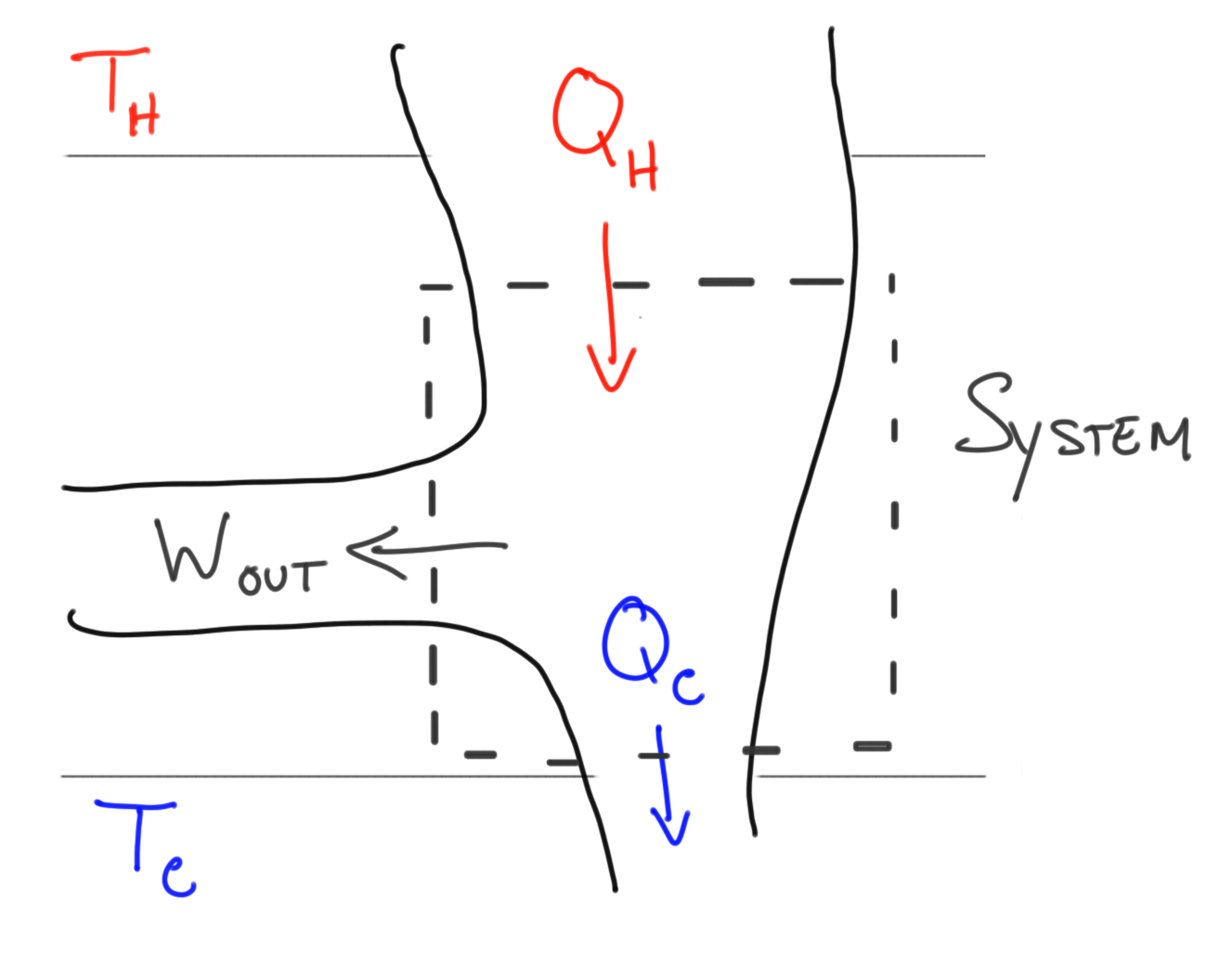
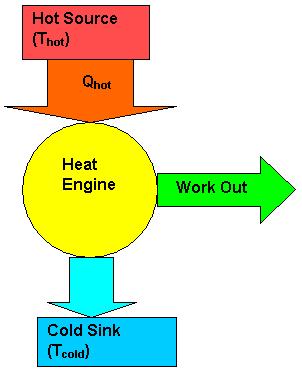
Mathematical
$\Delta E = Q+W$
$PV=NK_{b}T$
Efficiency: $ e = \frac{|\sum W|}{\sum Q_{in}}$
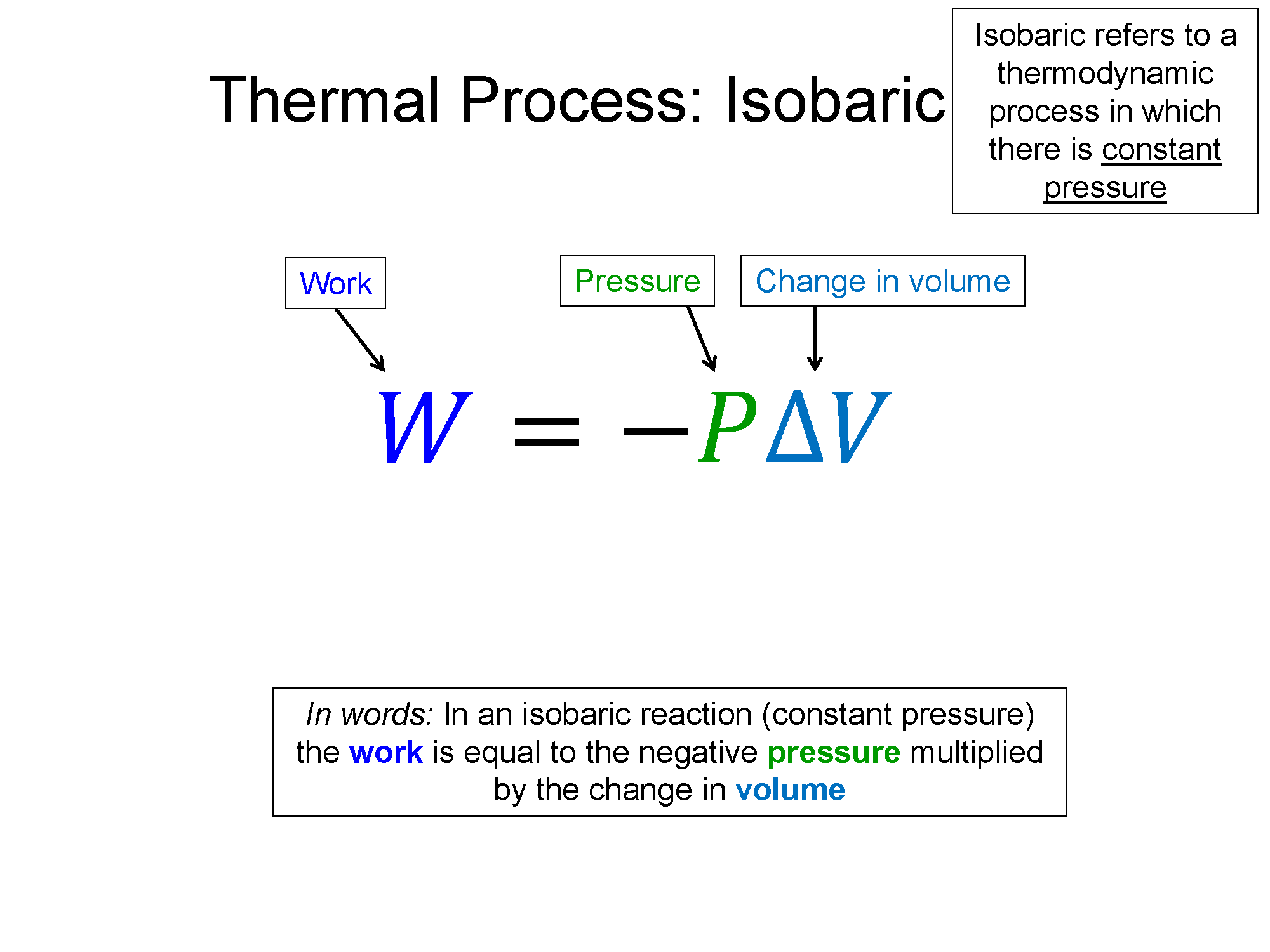
Isobaric
$\Delta P = 0$, then $\Delta V \propto \Delta t$
$W = P \Delta V$
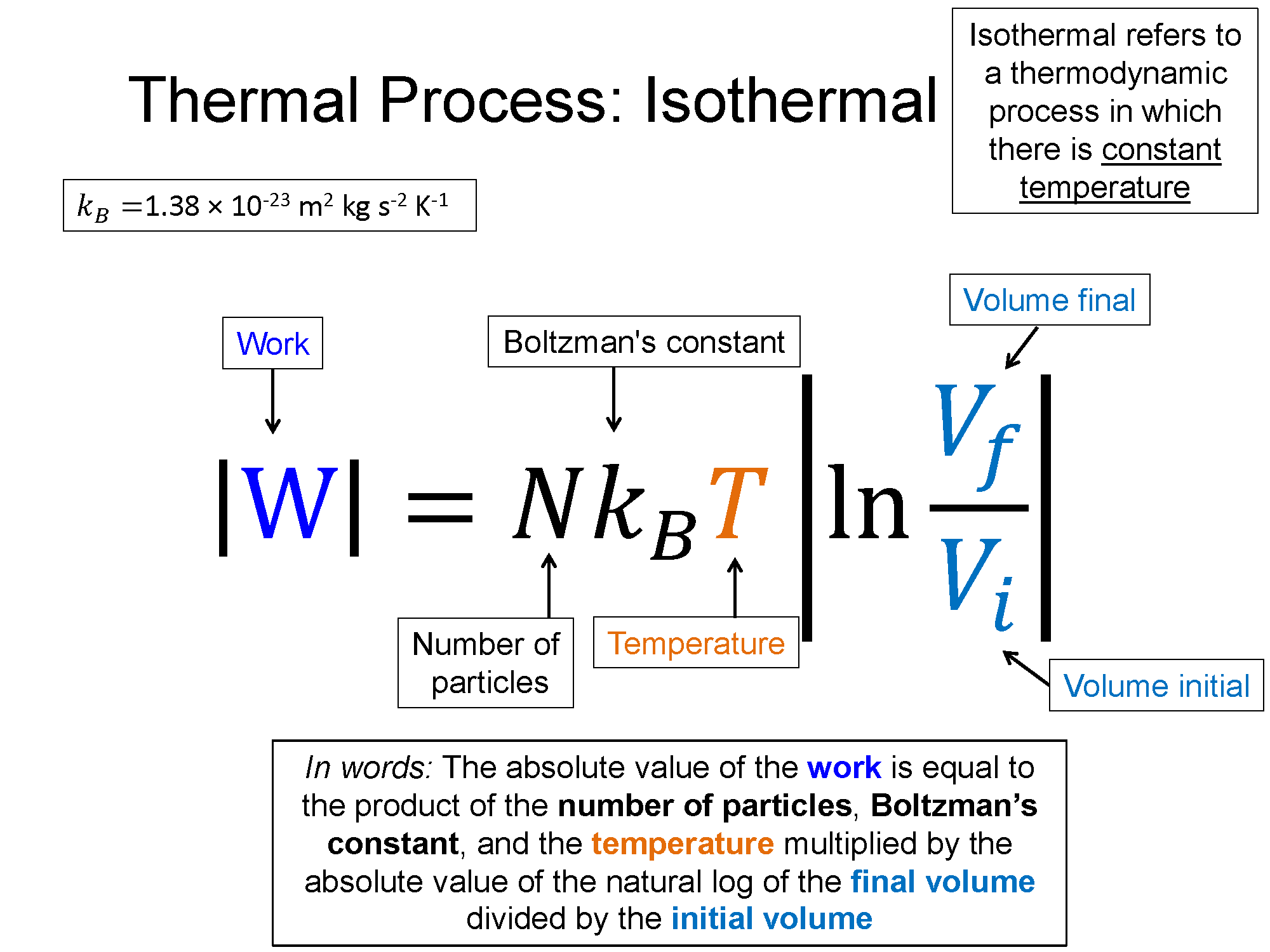
Isothermal
$\Delta T = 0$, then $P \propto \frac{1}{V}$
$W = \frac{3}{2}nT ln(\frac{V_{f}}{V_{i}}))$
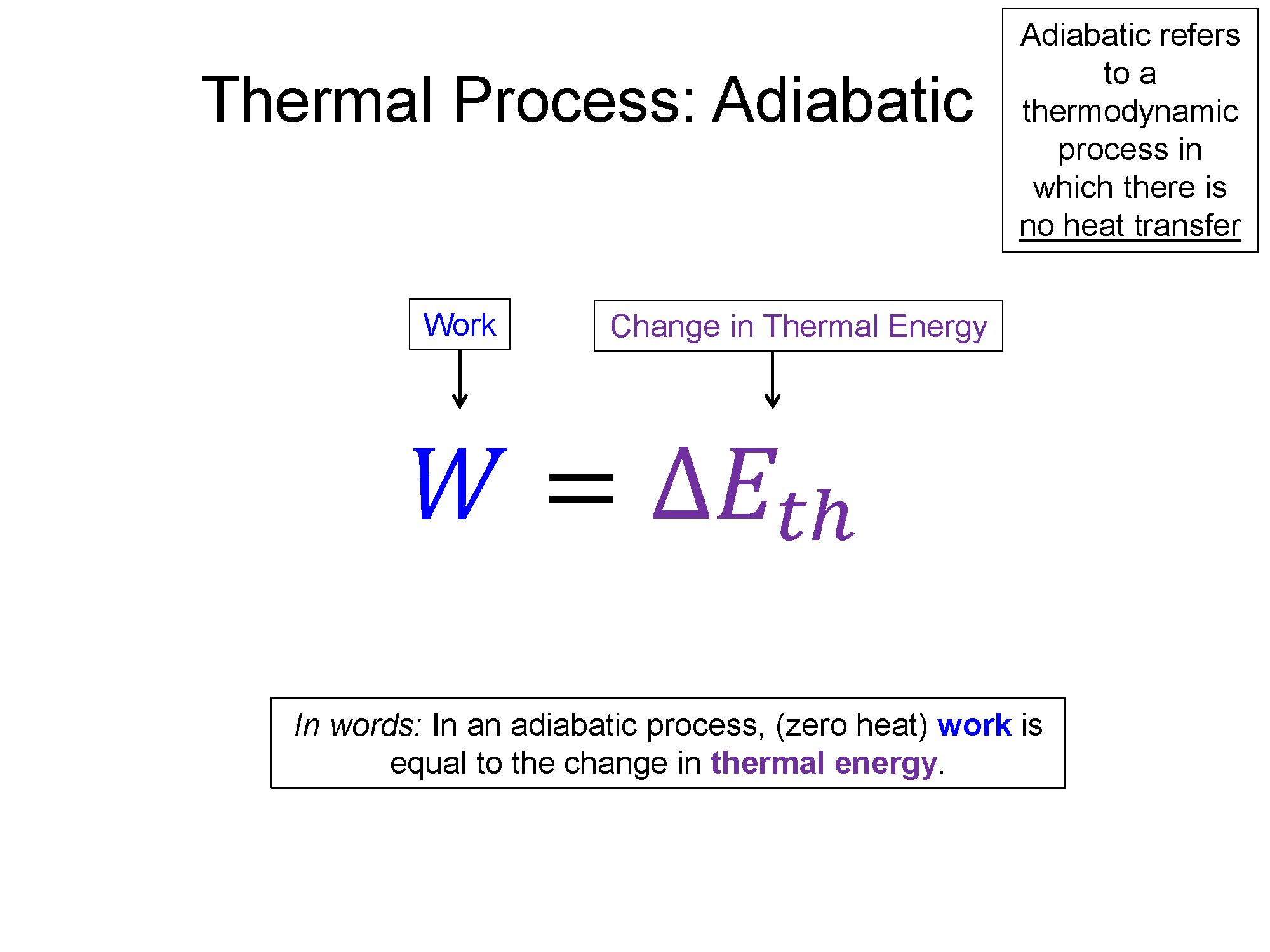
Adiabatic
$Q=0$, then $\Delta E = W$
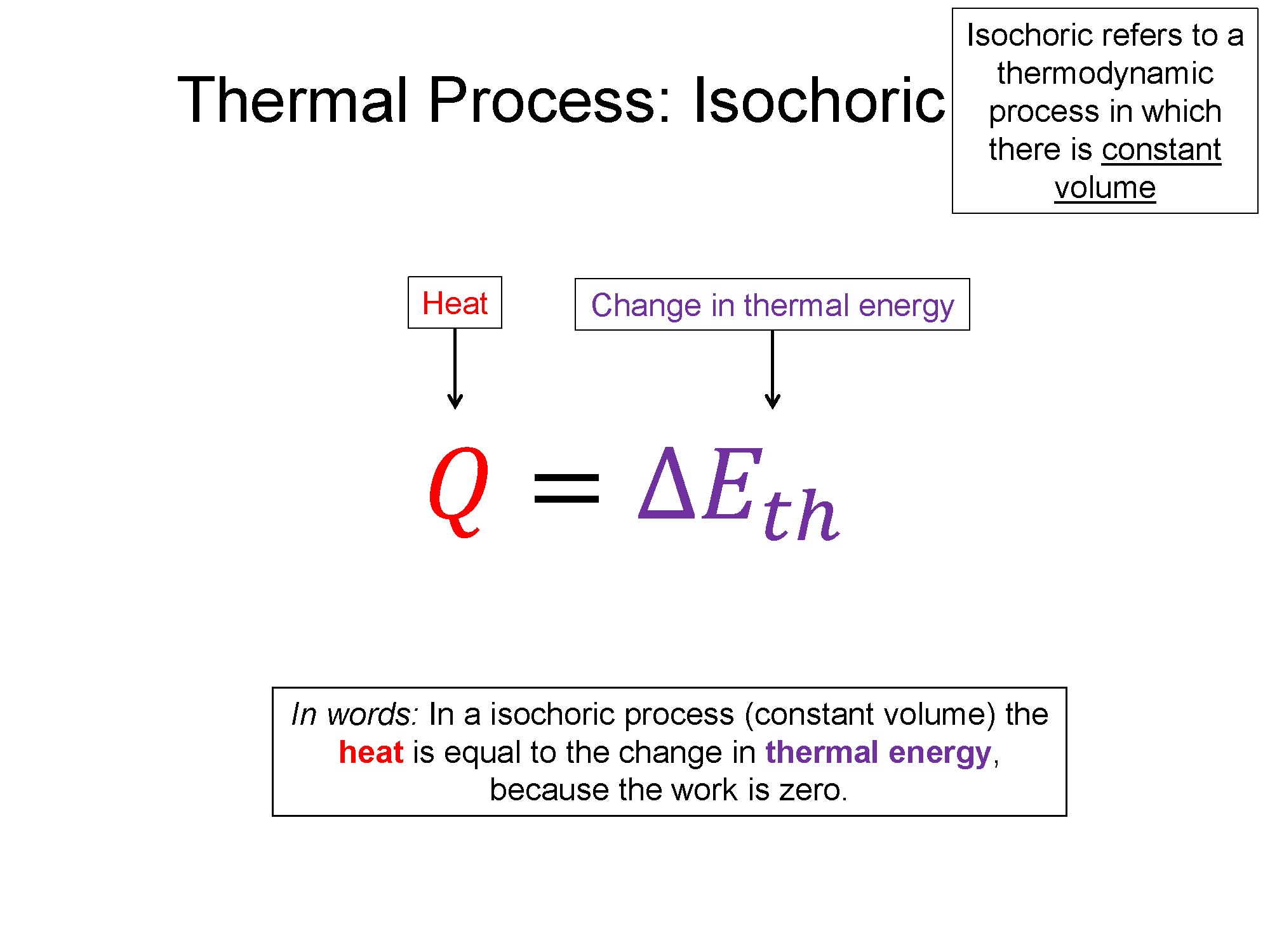
Isochoric
$\Delta V = 0$ and $W=0$
Totale energy ($E$), Heat ($Q$), Work ($W$), Efficiency ($e$), Pressure ($P$), Volume ($V$), Time ($t$), Temperature ($T$),
Number of moles ($n$)



Graphical
1-2 Isobaric, 2-3 Isothermal
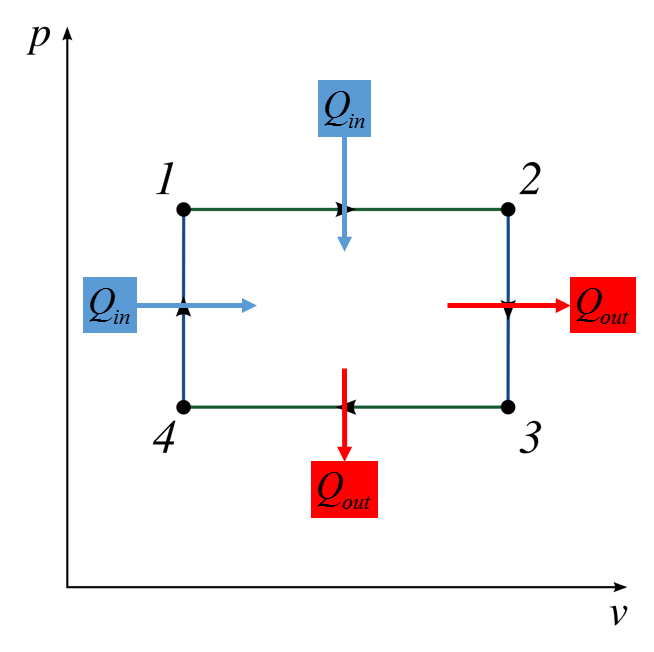
Descriptive
Here is a link to a description of the Carnot Cycle from Hyper Physics. This is an ideal description of a perfectly efficient cycle.
Experimental