The ideal gas law is a model that explains the observed relationships between thermodynamic quantities, such as temperature and pressure, of a lot of different gases. It was discovered experimentally, which is why it's called a law. For a gas to behave ideally, the particles the gas is comprised of must not interact, meaning they do not run into each other. This means that not all gases behave ideally and there is a degree to how ideal a gas is.
Thermodynamic state variables characterize the state of a thermodynamic system. The ideal gas law is a(n emperically derived) relationship between these variables.
This introduction to the ideal gas law from crash course chemistry is a great video to start this section.
Pre-lecture Study Resources
Watch the pre-lecture videos and read through the OpenStax text before doing the pre-lecture homework or attending class.
BoxSand Introduction
Thermodynamics | Ideal Gas Law
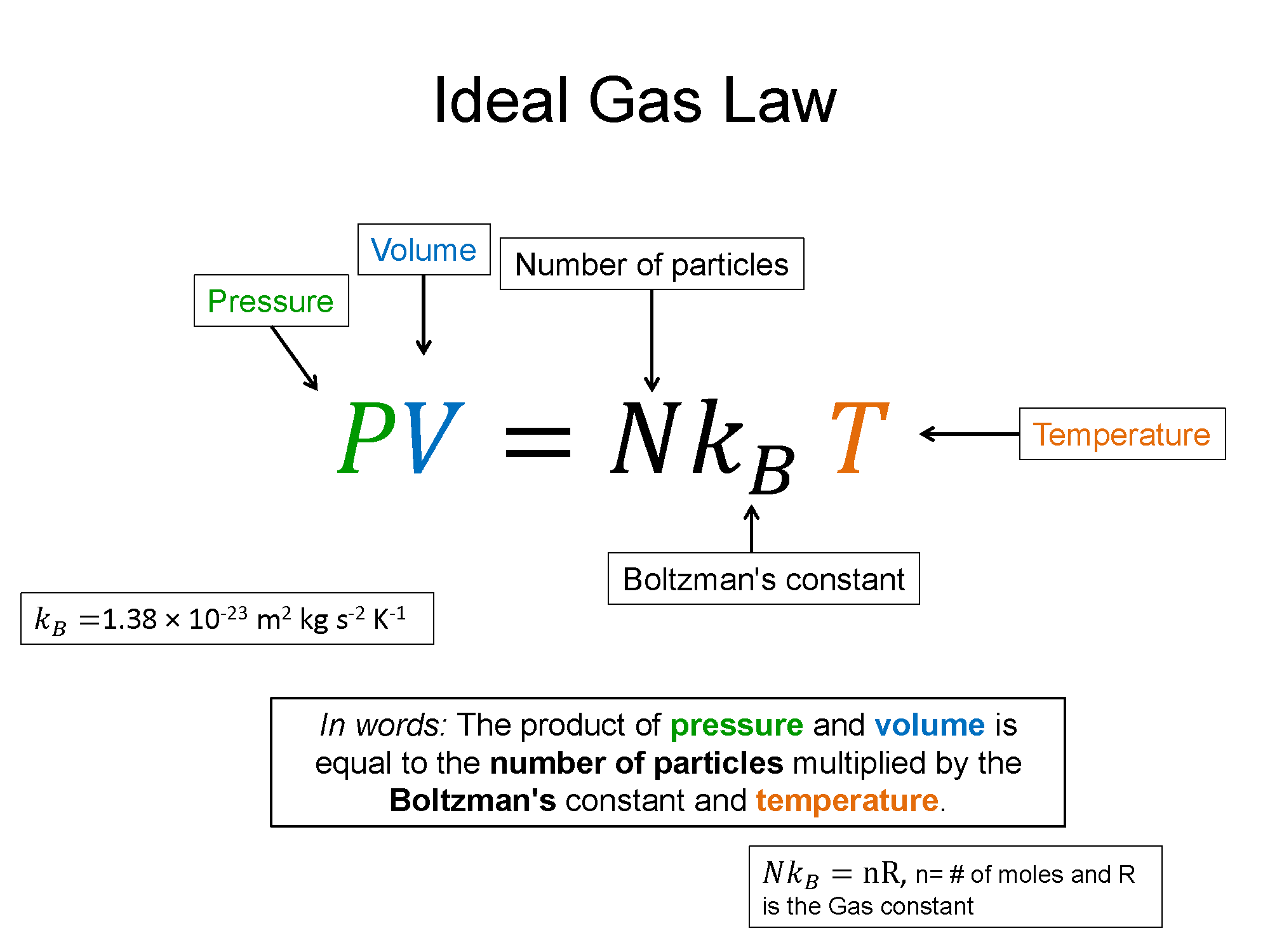
The Ideal Gas Law was first understand empirically through experimentation. It relates the thermodynamic state variables of temperature (T), pressure (P), volume (V), and number of particles (N). Since it is an equation comprised of variables that describe the state of the system, it is call an equation of state. Theoretically if a gas is truly ideal, that means the particles in the gas do not interact. There are other equations of state for gases that do not behave ideally. The ideal gas equation in physics is typically written as follows.
$PV=Nk_B T$, where kB is Boltzman's constant
Alternatively there is a form more typically seen in chemistry of $PV=nRT$. Here n represents the number of moles of particles in the gas and R is the Rydberg constant. Either form is valid and which one you use depends on what information is given. Either Way, since they are equivalent forms, then that must mean that $Nk_B = nR$, a useful relationship in other topics of thermo such as the kinetic theory of gases.
The graph is a 3D depiction of the ideal gas relationship with projections onto 2D surfaces.
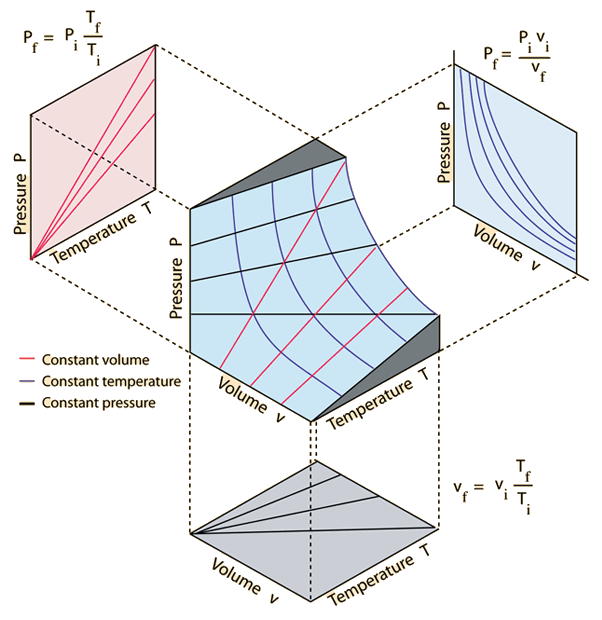
*Graphic by Hyperphysics
Key Equations and Infographics
Now, take a look at the pre-lecture reading and videos below.
BoxSand Videos
Required Videos
Suggested Supplemental Videos
OpenStax Reading
OpenStax Section 13.3 | The Ideal Gas Law
OpenStax Section 13.5 | Phase Changes
OpenStax Section 13.6 | Humidity, Evaporation, and Boiling
Fundamental examples
1. An ideal gas is sitting inside a container. (a) If the temperature of the gas is constant and the pressure of the gas quadruples, how does the volume change? (b) If the volume triples and the temperature is halved, what happens to the pressure?
2. 10 mol of helium are in a 15 L cylinder. The pressure gauge on the cylinder reads 65 psi. (a) What is the temperature of the gas in celsius? (b) What is the average kinetic energy of a helium atom?
3. A container holds an ideal gas at 20 degrees Celsius. The gas is composed of $10^{24}$ monatomic particles. (a) 1000J of thermal energy is added to the gas. What is the new temperature of the gas? (b) If, instead, the container holding the ideal gas expands to be double its original size and the pressure remains constant, what is the final temperature of the gas?
Short foundation building questions, often used as clicker questions, can be found in the clicker questions repository for this subject.
Post-Lecture Study Resources
Use the supplemental resources below to support your post-lecture study.
Practice Problems
BoxSand's multiple select problems
BoxSand's quantitative problems
Recommended example practice problems
- Openstax, many examples throughout, 3 conceptual questions, and 17 practice problems, Website Link
-
Good Worksheet of 5 questions pertaining to the Ideal Gas Law, PDF Link
-
8 problem worksheet on Gas Laws. PDF Link.
For additional practice problems and worked examples, visit the link below. If you've found example problems that you've used please help us out and submit them to the student contributed content section.
Additional Boxsand Study Resources
Additional BoxSand Study Resources
Learning Objectives
Summary
Summary
Atomistic Goals
Students will be able to...
Microscopic view of matter
- (UPMF) Construct a microscopic model of a solid using an analogy of particle masses connected by springs.
- Construct a microscopic model of a liquid as a collection of loosely bonded masses able to roll around each other.
- Construct a microscopic model of a gas consisting of a set of rarely interacting particles.
- (UPMF) Construct a model of microscopic particle interactions arising from electromagnetic forces.
Macroscopic view of matter
- Employ the fact that solids retain their shape unless deformed by a relatively large force.
- Employ the fact that a liquid in a gravitational field will take the shape of a container when poured into it.
- Employ the fact that a gas expands to distribute itself in the container it occupies.
- Distinguish between the density of solids, liquids, and gasses.
- Define pressure as a perpendicular force component per area.
- Define volume as having dimensions of length cubed.
- Explain how density and compressibility are related.
- Distinguish between the compressibility of solids, liquids, and gasses.
- Identify when the constant density and compressibility approximation breaks down (e.g. water at the bottom of the ocean).
Connecting Microscopic and Macroscopic views of matter
Kinetic theory of monatomic gases
Equations of state and state variables
Ideal gas law
- Demonstrate that the macroscopic state of the system arises from a microscopic ensemble of particles.
- Construct a model where an ensemble of microscopic particles' kinetic energy results in a macroscopic overall temperature.
- Construct a model of pressure arising from an ensemble of microscopic particle collisions, where momentum in transferred, resulting in a macroscopic force per area.
- Demonstrate that the average microscopic kinetic energy of a particle is a function of the average mass and average (root mean squared) speed.
- Demonstrate that the total thermal energy of a system is the sum of the microscopic translational kinetic energy of all the particles.
- Identify three modes of microscopic kinetic energy: translational, vibrational, and rotational.
- Show that a monatomic gas only possess the translational mode of kinetic energy.
- Apply the Boltzmann postulate to connect the microscopic translational kinetic energy to macroscopic observable of temperature.
- Show that the total thermal energy is a function of total number of particles and temperature of the gas.
- Convert between number of particles and number of moles using Avogadro's number.
- Convert between number of particles and number of moles using the gas constant R and Boltzmann's constant kB.
- Differentiate between open, closed, and isolated systems, and how they apply to the exchange of energy and particle number between systems.
- Explain that state variables are quantities that characterize the thermodynamic state of a system and are used to construct the equation of state.
- Explain that an equation of state is a function that relates state variables and defines the state of the system in equilibrium.
- Differentiate between extrinsic and intrinsic state variables, where extrinsic scales with the number of particles and intrinsic does not.
- Define pressure, volume, number of particles, and temperature as state variables.
- Explain that there are other state variables including thermal energy, chemical potential, entropy, magnetization, degrees of freedom(?), … etc.
- Identify that the ideal gas law is an equation of state that contains the state variables, pressure, volume, temperature, and number of particles.
- Define a system as an ideal gas if (i) it has particles that do not interact with each other or (ii) all interactions are elastic collisions.
- Recognize an ideal gas is an assumption not always relevant.
- Identify when a system can be approximated as an ideal gas by justifying the density as sufficiently low so collisions are rare, or the particles making up the gas are not easily deformed.
- Recognize that there are more sophisticated equations of state to account for increasingly complicated intrasystem interactions, such as the Van der Waals equation of state that accounts for particle size and polar interactions.
- Apply proportional reasoning using the ideal gas law.
- Describe the features of an inverse relationship, i.e. pressure and volume at constant number of particles and temperature.
PV-diagrams
- Interpret a plot of pressure vs. volume where each point on the plot represents a different equilibrium state of the system.
- Construct and interpret a PV-diagram for a given equilibrium state of a system, or changes in the state of the system between two equilibrium points.
YouTube Videos
The Pre-Med Academy introduces the ideal gas law in a straight forward way.
Professor Dave Explains the ideal gas law in a very clear manner. At the end of the video he will stop for a concept check. This is a good opportunity for practice! Pause the video and give the problems a try before he gives the answers.
Doc Schuster gives a good introduction to the Ideal Gas Law.
Crash Course has a strategy video for solving Ideal Gas Law problems.
https://www.youtube.com/watch?v=8SRAkXMu3d0
Tyler DeWitt works through some ideal gas problems.
Other Resources
This link will take you to the repository of other content related resources.
Simulations
Here is the PhET Simulation for exploring gas properties. While using the app, think about how the Ideal Gas Law can be used to describe what is happening. Even consider a situation first using the Ideal Gas Law, then try to confirm your predictions using the simulation.
This simulation brings together the ideal gas law in a fun easy way to understand.
For additional simulations on this subject, visit the simulations repository.
Demos
Here are several demonstrations with the ideal gas law.
For additional demos involving this subject, visit the demo repository
History
Oh no, we haven't been able to write up a history overview for this topic. If you'd like to contribute, contact the director of BoxSand, KC Walsh (walshke@oregonstate.edu).
Physics Fun
Other Resources
Resource Repository
Hyperphysics provides us with an interactive concept map for the Ideal Gas Law. All these bubbles will be relevent throughout the section, start at the top with "Ideal Gas Law"
Boston University's page on the ideal gas law is a quick read,
Other Resources
This link will take you to the repository of other content related resources.
Problem Solving Guide
Use the Tips and Tricks below to support your post-lecture study.
Assumptions
All T's written in all equations given in this class will assume the temperature is measured in Kelvin, and you NEED to use Kelvin typically, even when you will more often be given a temperature in Celsius. The only exception to this is when T has a Delta in front of it, in that case, you may use Kelvin or Celsius since the difference between temperatures in both systems will be the same (Celsius is just a linearly shifted version of Kelvin, and vice versa). However, you CANNOT use Fahrenheit still, the conversion to/from Fahrenheit isn't as simple as a shift, so it doesn't work the same way as the other two.
Checklist
Ideal Gas Law problems typically require you to do some or all of the following:
1. Proportional reasoning using the ideal gas law $PV=nRT$
2. Unit conversion
3. Relating changes in the thermodynamic variables in the ideal gas law to changes in the thermal energy $E_{th}$ of the system.
Identify which of the 3 tasks the problem is asking you to do (often the answer is all 3 of them). Proportional reasoning is something you should already be familiar with; employ your favorite tactic. If you are struggling with proportional reasoning, show up to office hours and ask a TA for help as soon as possible, they'll be happy to help!
For unit conversions, just take your time and make sure you have the correct definitions down. If you aren't sure, for example, how to convert $1 m^2$ into $cm$, just write it out: $1 m^2 = (1 m)(1 m) = (10^{-2} cm)(10^{-2} cm) = 10^{-4} cm$ which makes things more clear than trying to jump from $1 m^2 = 10^{-4} cm$
Misconceptions & Mistakes
The ideal gas law is an approximation. There is no such thing as an ideal gas (although some types of particles, such as noble gasses, come close). But it is a very good approximation for most particles, especially at standard temperature and pressure.
Pro Tips
- $Nk_{B} = nR$.
- Always convert temperatures to Kelvin. At the end of the problem you might be asked to report the answer in other units, but whenever you use the ideal gas law to make calculations you'll need to use temperatures in Kelvin, so you may as well be in the habit of converting right away so you don't make a calculator mistake.
- For lots of ideal gas problems, the trick is reading the problem carefully. You'll often be explicitly given the value of one thermodynamic variable, then something about the way the question is phrased should lead you to assume one of the other thermodynamic variables is constant. The problem then reduces to just doing algebra to solve for one of the variables in the Ideal Gas Law.
- Liters go with atmospheres; meters go with pascals. A helpful mnemonic is to remember that pascals are defined as a newton of force applied over a meter squared area, which gives you a pascal: $P = \frac{F}{N} = \frac{N}{m^2} = Pascals$. So meters and pascals are naturally associated in that way.
- Even if they are packaged differently, most problems in this question are best solved with proportional reasoning. Nearly every problem has some form of a couple thermodynamic variables staying constant and another changing, and asking what happens to the remaining ones (e.g. $P$ and $N$ are constant but $V$ increases; how does $T$ change?).
Multiple Representations
Multiple Representations is the concept that a physical phenomena can be expressed in different ways.
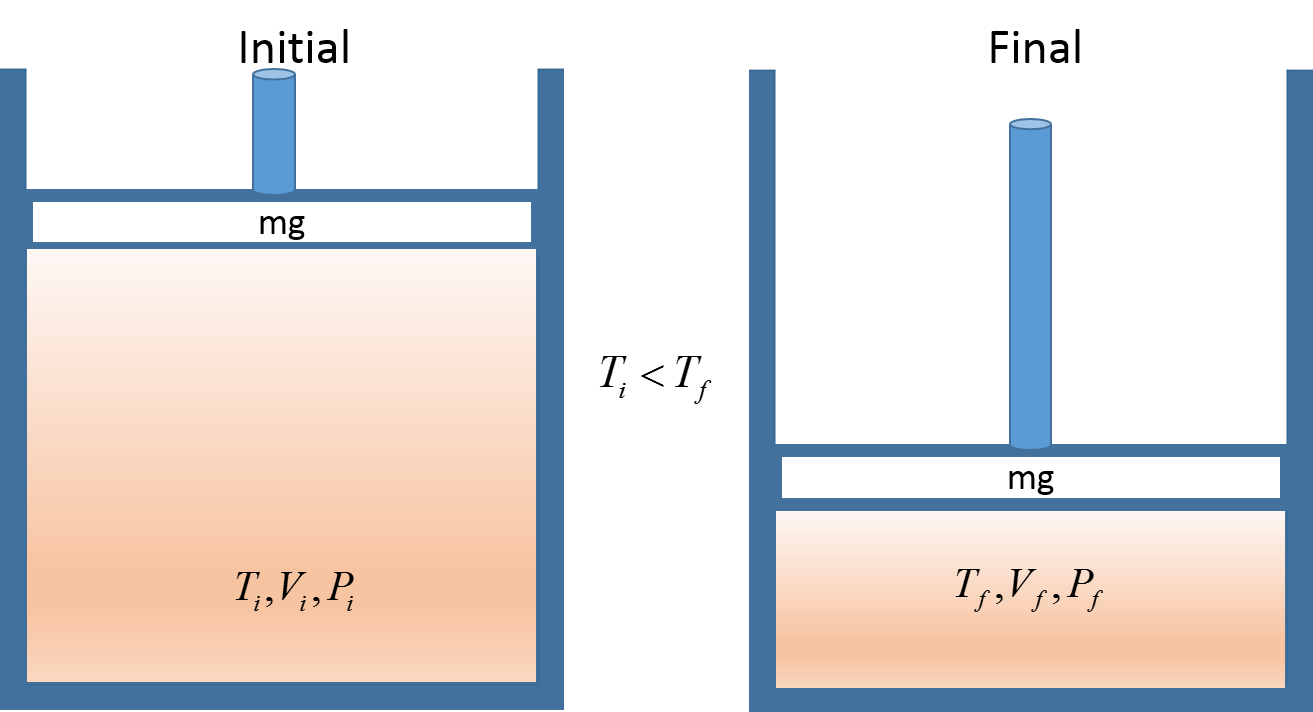
Physical
The initial and final states of two pistons where the pressure increases from intial to final thus increasing the final temperature. This is one physical representation we might use to solve an ideal gas law problem.
Mathematical
$PV=nRT = N K_b T$
Pressure ($P$), Volume ($V$), Numer of mols ($n$), Rydberg constant ($R$), Temperature ($T$), Numer of particles ($N$),
Boltzman constant ($K_{b}$)

Graphical
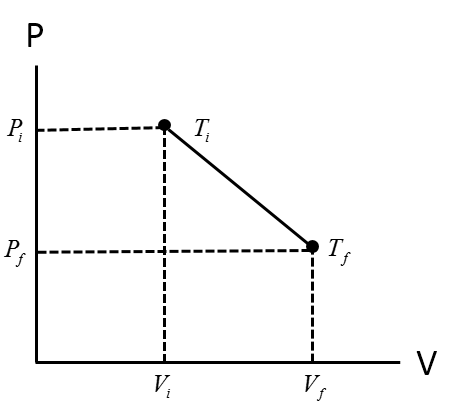
The following plot describes how the pressure and volume of a system respond to the state of the system temperature.
Descriptive
The ideal gas law describes the relationship between pressure (P), volume (V), and temperature (T). Namely, pressure and volume are inversely proportional to each other when the temperature is held constant. In addition, there is a direct relationship between pressure and temperature when the volume is held constant, or conversely there is a direct relationship between volume and temperature when the pressure is held constant.
Experimental
The ideal gas law was derived from three different laws: Boyle's law, Charle's law, and Avogadro's law. The following three videos give some insight into each law separately.
Boyle's law
Charle's law
Avogadro's law