Objects can possess energy in many forms but this section is only going to consider the energy from the translational motion of the system. This motional energy is called kinetic energy ($K = \frac{1}{2} m v^2$) and notice it is a scalar quantity. It is true that velocity is a vector quantity but when you square it, all direction is lost. Objects can also exchange energy with other objects through the concept of Work ($W$). The Work-Kinetic Energy theorem relates the change in kinetic energy of the system to the work performed on the system.
Check out this song about all the forms of energy.
Pre-lecture Study Resources
Read the BoxSand Introduction and watch the pre-lecture videos before doing the pre-lecture homework or attending class. If you have time, or would like more preparation, please read the OpenStax textbook and/or try the fundamental examples provided below.
BoxSand Introduction
Work and Energy| Work and Kinetic Energy Theorem
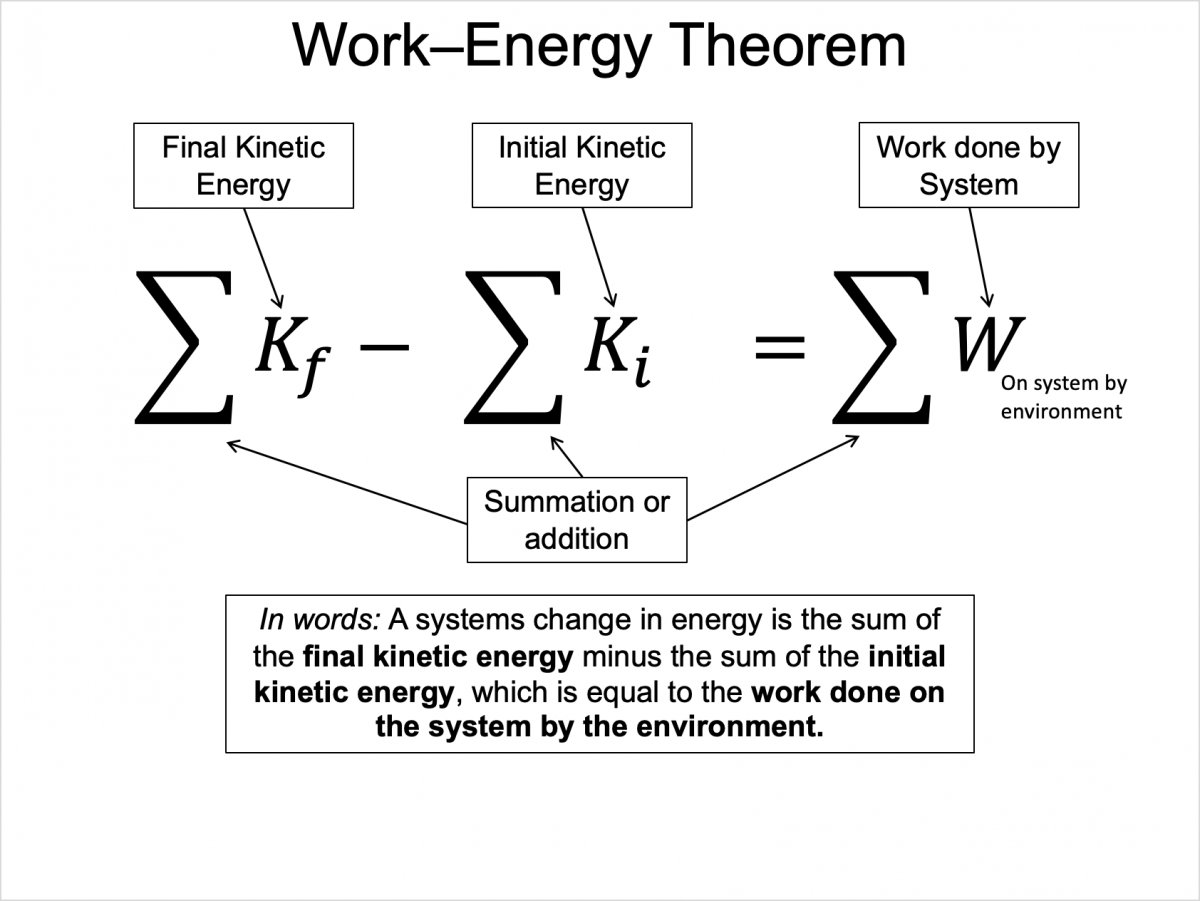
Consider the motion in 1D and the kinematics equation, $v_{fx}^2 = v_{ix}^2 + 2a_x \Delta x$, and Newton's 2nd Law with constant acceleration in one dimension, $\sum F_x = m a_x$. A simple substitution, and minor rearrangements, of the acceleration from the 2nd law into the kinematics equation yields:
$\frac{1}{2}m v_{fx}^2 - \frac{1}{2}m v_{ix}^2 = \sum F_x \Delta x$
It appears that forces acting over a distance changes the velocity of objects according to the equation above. As it turns out, this manipulation of equations will be of great benefit in analyzing the motion of objects, so we define new terms for the expressions shown in the above equation.
Linear Kinetic Energy (K): $\frac{1}{2}m v^2$.
Work (W): $F_x \Delta x$.
Using our newly defined terms, we now can write what we call, the Work-Kinetic Energy theorem as:
$K_f - K_i = \sum W$
This expression lets you see the heart of the Work-Kinetic Energy theorem, namely that a system's change in energy is due to work from external forces performed on the system. The theorem is often rearranged so that it can be interpreted as: take the initial kinetic energy of the system and add the net work acting on the system and this is equal to the final kinetic energy of the system.
$K_i + \sum W = K_f$
**Note: K and W are scalar quantities! The above arguments are shown in one dimension. Continue reading further in this section to learn how to generalize if our forces, displacements, or velocities are in more than one dimension.
Key Equations and Infographics


Now, take a look at the pre-lecture reading and videos below.
BoxSand Videos
Required Videos
Suggested Supplemental Videos
OpenStax Reading
OpenStax Section 7.1 | Work: The Scientific Definition
OpenStax Section 7.2 | Kinetic Energy and the Work-Kinetic Energy Theorem
Fundamental examples
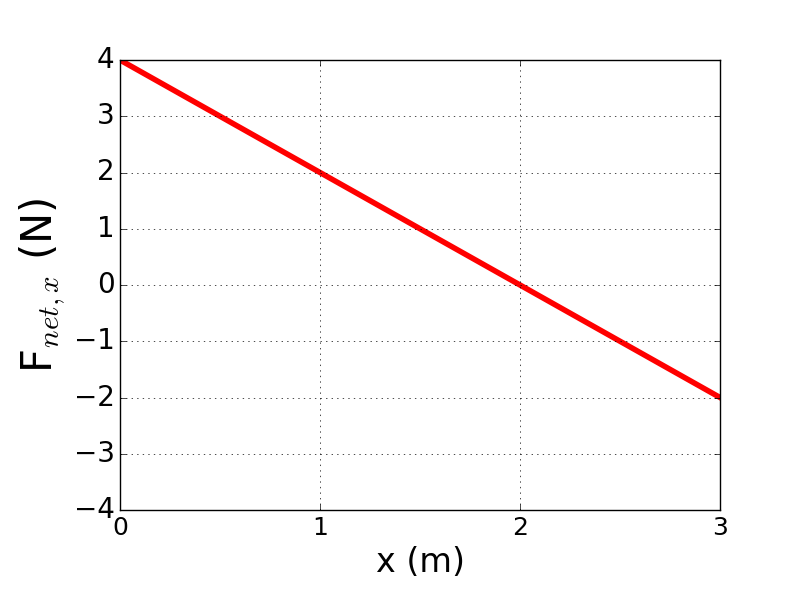
1. An object initially has a kinetic energy of $7 \, J$. A force is then applied on the object as described in the graph below. What is the final kinetic energy of this object after the force acts on the object over $3 $ meters?
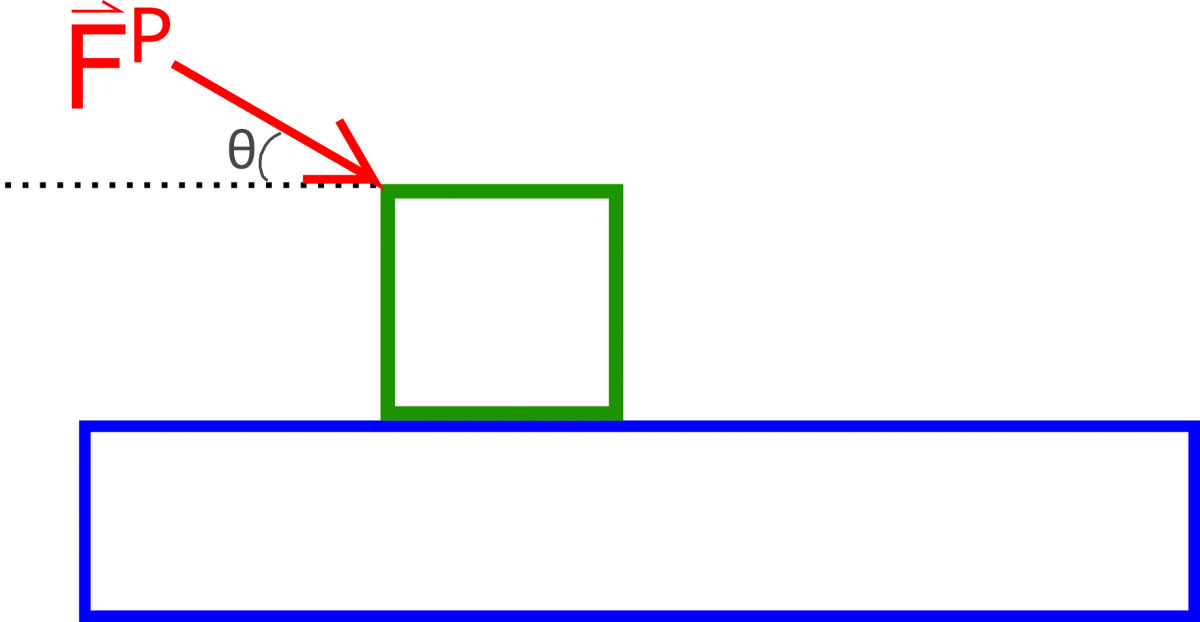
2. A box of mass $4 \, kg$ initially at rest sits on top of a frictionless table. A constant force of magnitude $3 \, N$ is then applied to the box as shown in the image below. What is the change in kinetic energy of the box if the force is applied over a distance of $5 \, m$?

3. A box of mass $4 \, kg$ initially at rest sits on top of a frictionless table. A constant force of magnitude $3 \, N$ is then applied to the box as shown in the image below. What is the change in kinetic energy of the box if the force is applied over a distance of $5 \, m$?
CLICK HERE for solutions.
Short foundation building questions, often used as clicker questions, can be found in the clicker questions repository for this subject.
Post-Lecture Study Resources
Use the supplemental resources below to support your post-lecture study.
Practice Problems
Recommended example practice problems
BoxSand's Quantitative Practice Problems
BoxSand's Multiple Select Problems
- BoxSand Practice Problems
- Openstax has practice problems toward the end of each section, Website Link
- Indiana University Physics: 3 basic problems, Website Link, their solutions, Website Link
- Physics Classroom 1,3,5,6,7,11,12, 18, Website Link
For additional practice problems and worked examples, visit the link below. If you've found example problems that you've used please help us out and submit them to the student contributed content section.
Additional Boxsand Study Resources
Additional BoxSand Study Resources
Learning Objectives
Summary
Students are introduced to the concept of kinetic energy and how work is a mechanism for systems to exchange energy. The goal is construct the work-energy theorem to analyze systems which requires knowledge of the dot product.
Atomistic Goals
Students will be able to...
- Find the kinetic energy for a system.
- Identify which quantities are scalars and which are vectors.
- Define the work-energy theorem and explain how work is a mechanism to transfer energy between systems.
- (UPMF) Differentiate between internal and external work.
- Demonstrate that energy involves forces applied over distances and momentum involves forces applied over time.
- (UPMF) Find the area under a net force vs displacement curve and set that equal to the work on the system.
- Identify that work is a dot product between the force and the change in position.
- Determine whether work is positive or negative based on forces and displacement.
- Determine whether (net) work is positive or negative based on the change in kinetic energy.
- Identify that a dot product depends on the magnitude of the two vectors and the smallest angle between them.
- Explain how a dot product shows how much one vector points in the same direction as another using the projection method.
- (UPMF) Use a vector operation diagram to visualize the dot product between two vectors.
- Calculate work by applying the dot product in the mathematical form via magnitudes and smallest angles.
- Calculate work by applying the dot product in the mathematical form of summation of products of components.
- Construct the work-energy theorem in the mathematical representation to analyze physical systems.
YouTube Videos
Simulations
Check out this interactive simulation on kinetic energy. Note that the external work in this case is due to friction if it is turned on.
Build your own roller coaster and test to see if it has enough initial energy to get through the entire track.
For additional simulations on this subject, visit the simulations repository.
Demos
Simple work enegry theorem demonstration with a toy car and motion detector,
For additional demos involving this subject, visit the demo repository
History
Physics Fun
Oh no, we haven't been able to post any fun stuff for this topic yet. If you have any fun physics videos or webpages for this topic, send them to the director of BoxSand, KC Walsh (walshke@oregonstate.edu).
Other Resources
This link introduces the concept of kinetic energy.
This link provides an introduction to the concept of work.
Other Resources
This link will take you to the repository of other content related resources.
Problem Solving Guide
Use the Tips and Tricks below to support your post-lecture study.
Assumptions
Checklist
1. Read and re-read the whole problem carefully.
2. Visualize the scenario. Mentally try to understand what the object(s) are doing and what forces are acting on them.
3. Identify the system you wish to analyze; This may include one or more objects if coupled to one another.
4. Write down all of your knowns and unknowns.
5. Identify all the forces acting on your object(s). Include a FBD to help keep track of all the forces.
a. If a force acting on an object is not constant, (i.e. it depends on position), then consult a force vs displacement graph to calculate the work.
6. Determine the displacement of the object.
7. Calculate the work done by each force.
a. For forces that are not parallel or perpendicular, draw a vector operation to help determine the angle between the force and displacement.
b. Double check you have the right sign of work.
8. Use the work-kinetic energy theorem $KE_i + \sum W = KE_f$ to solve for the relevant quantities.
9. Evaluate your answer; make sure units are correct and the results are within reason.
Misconceptions & Mistakes
Kinetic Energy
- Remember, kinetic energy is not related to size, only mass and velocity.
- Kinetic energy and work are both scalar quantities; do not attempt to split them up into components like vectors.
- Kinetic energy occurs whenever an object has a velocity, no matter the reason for the motion.
- You can't always assume that higher velocity (or larger mass) means larger kinetic energy. You must look at both the mass and the velocity of the object.
- A big misconception is that doubling the velocity doubles the kinetic energy. When you actually look at the equation: $KE=\frac{1}{2}mv^2$ you can see that the velocity is squared thus if you double the velocity you actually increase the kinetic energy by that squared factor.
Work
- Just because a large force is applied does not necessarily mean work was done. The object must move for to have been done.
- Work can be negative or positive- depending on whether the system is doing work (-) or whether work is being done on the system (+).
- Objects do not possess work; work is a mechanism for interacting objects to exchange kinetic energy.
- Think about whether it is being done on the system or by the system and use that to double check the sign of the work.
- If the force acting over a distance is not constant, you can not just use the maximum value of the force. You must consult a force vs distance graph and use the area under the curve to estimate the work done.
Pro Tips
- If given information about forces and displacements, start to think about work-kinetic energy.
- For forces that are not parallel or perpendicular to displacements, draw a vector operation to ensure you are using the correct angle for the dot product between the two vectors.
Multiple Representations
Multiple Representations is the concept that a physical phenomena can be expressed in different ways.
Physical
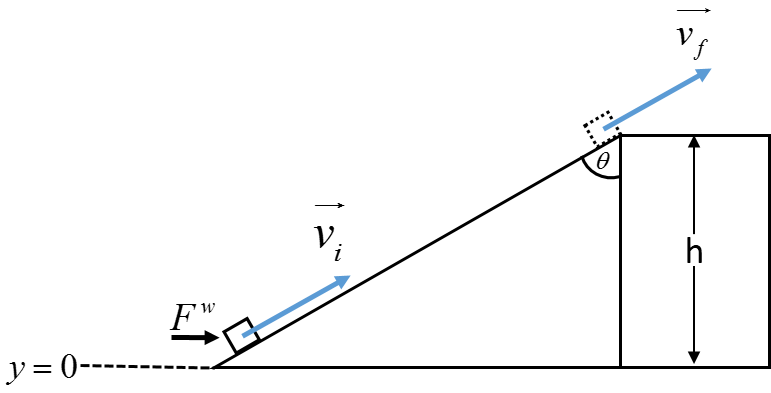
A block is launched up a frictionless ramp with initial velocity $\vec{v_{i}}$.
Mathematical
$ \sum K_{i} + \sum W_{external} = \sum K_{f}$
$ K = \frac{1}{2} mv^{2}$
$W = \bar{\vec{F}_{ext}} \cdot \Delta \vec{r}$



Graphical
 .
.
Descriptive
A block is launched up a frictionless ramp, as shown in physical representation above, with an initial $\vec{v_{i}}$. The block travels up the ramp and continues across the level section. Once the block has been launched up the ramp, force due to gravity and the normal force will act upon the block. The force due to gravity will slow the box down, so gravity will do non-zero work on the block, while the normal force will do zero work on the block. If friction was present, then friction would also be doing work on the block and decelerate the block.
Experimental