Summary

The objective is to introduce vector mathematics in multiple representations through the use of physical quantities such as position, displacement, average velocity, and average acceleration.

Atomistic Goals

Students will be able to...

1. Identify if a physical quantity is a vector or a scalar.
2. Describe a vector using the descriptive, physical, and mathematical representation.
3. Convert between polar(magnitude and direction) and Cartesian coordinates (x & y).
4. Represent vectors using many standard notational representations, e.g. $\langle x, y \rangle$; $\hat{x} + \hat{y}$; and $\hat{i} + \hat{j}$.
5. Translate between the descriptive and physical representations of a vector.
6. Translate between the physical and mathematical representations of vector.
7. Multiply a vector by a scalar in the mathematical and physical representations.
8. Add vectors using the physical representation with the head-to-tail method or parallelogram method when tail-to-tail.
9. Add vectors using the mathematical representation.
10. Subtract vectors with the tools of vector addition.
11. Subtract vectors using the physical representation with the tail-to-tail method.
12. Subtract vectors using the mathematical representation.
13. Determine the summation (net) of a set of more than two vectors.
14. Manipulate vector equations using the rules of algebra.
15. (UPMF) Select between using vector algebra and geometrical methods when finding distances.
16. Recognize that multiplication and division of two vectors are not possible operations - advanced operations of dot and cross products will be presented when the physical situation warrants it.

Review and Vectors | Vector Operations

We have focused so much on creating introductions to the physics content we haven't had time to create text that reviews vectors. We do however have good videos on what you'll need to know starting this class. Check them out below in the drop down called BoxSand Videos. You can also check out the vectors sections of the OpenStax Textbook in the drop down below.

Section 3.2 of the OpenStax text book provides additional understanding of graphical methods of vector operations.

Section 3.3 of the OpenStax text book covers analytical methods of vector component decomposition and vector operations like addition and subtraction.

Vector Representations (25 min)

Vector Representations (25 min)

Vector Addition (13 min)

Vector Addition (13 min)

Additional Suggested BoxSand Videos

LAs Share | How Not to Suck at Physics

How Not to Suck at Physics (8 min)

LAs Share | How Not to Suck at Physics Part 2: Challenge Homework

How Not to Suck at Physics Part 2: Challenge Homework (4 min)

    1. Physics Classroom has a nice intro to Scalars and Vectors | Math Tools => Vectors => Web Resources

Doc Schuster has created a wonderful series on youtube to help students understand their physics. This video is a fairly in-depth example involving average velocity. This video also shows how you are not anchored to using the average velocity equation as it is given, you are free to preform any algebraic manipulation you would with any other equation.

https://www.youtube.com/watch?v=CaH57mVYhxU

    1. Check out the PhET simulation that helps you visualize adding vectors.

For additional simulations on this subject, visit the simulations repository.

 For additional demos involving this subject, visit the demo repository

Oh no, we haven't been able to write up a history overview for this topic. If you'd like to contribute, contact the director of BoxSand, KC Walsh (walshke@oregonstate.edu).

Oh no, we haven't been able to post any fun stuff for this topic yet. If you have any fun physics videos or webpages for this topic, send them to the director of BoxSand, KC Walsh (walshke@oregonstate.edu).

Check out the Physics Classroom's quick intro to Vectors vs. Scalars. Take the Check your Understanding quiz!

Resource Repository

This link will take you to the repository of other content on this topic.

Multiple Representations is the concept that a physical phenomena can be expressed in different ways. 

Physical

Physical Representations describes the physical phenomena of the situation in a visual way.

 

Let's examine some of the various vector operations we can do, with physical representations.

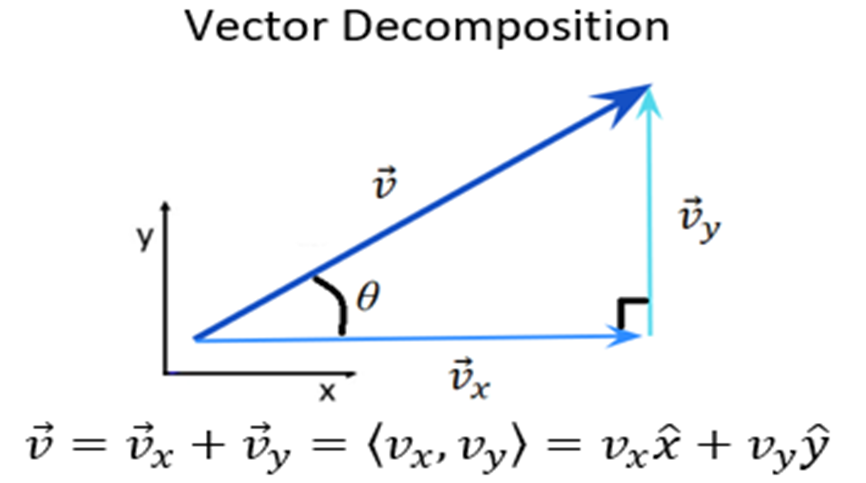
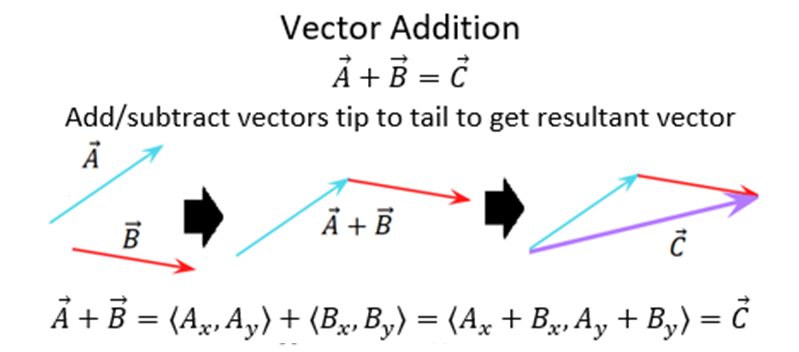
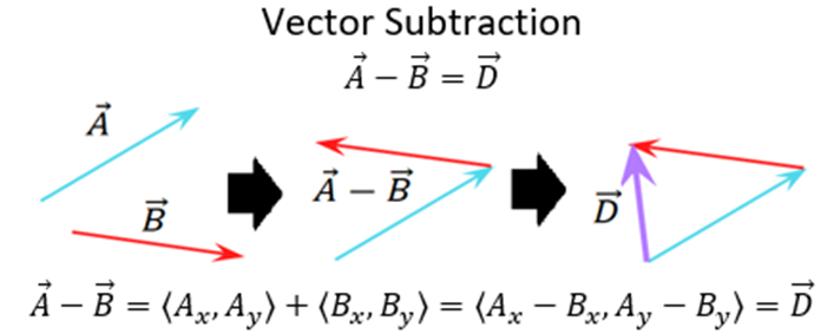
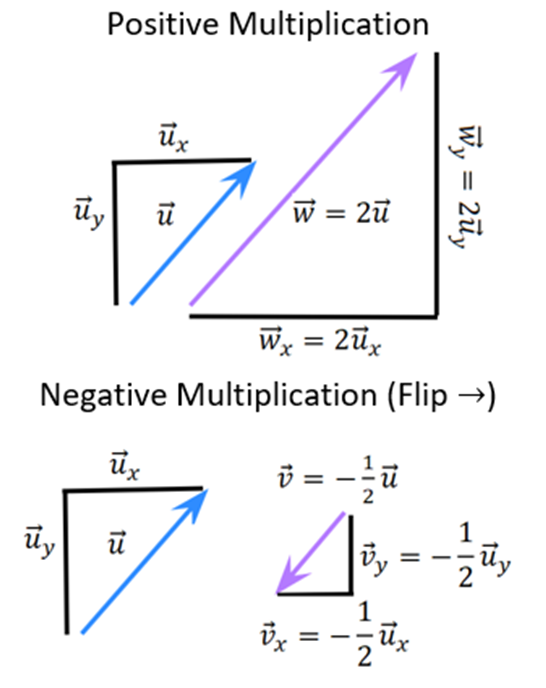
Mathematical

Graphical

Descriptive

Experimental

Check out the step by step Vector Review Worksheet below. There are questions intermixed with the review material. Try and work the problems before checking out the solutions.

          Vector Review Worksheet ======> Click HERE

          Vector Review Solutions ======> Click HERE

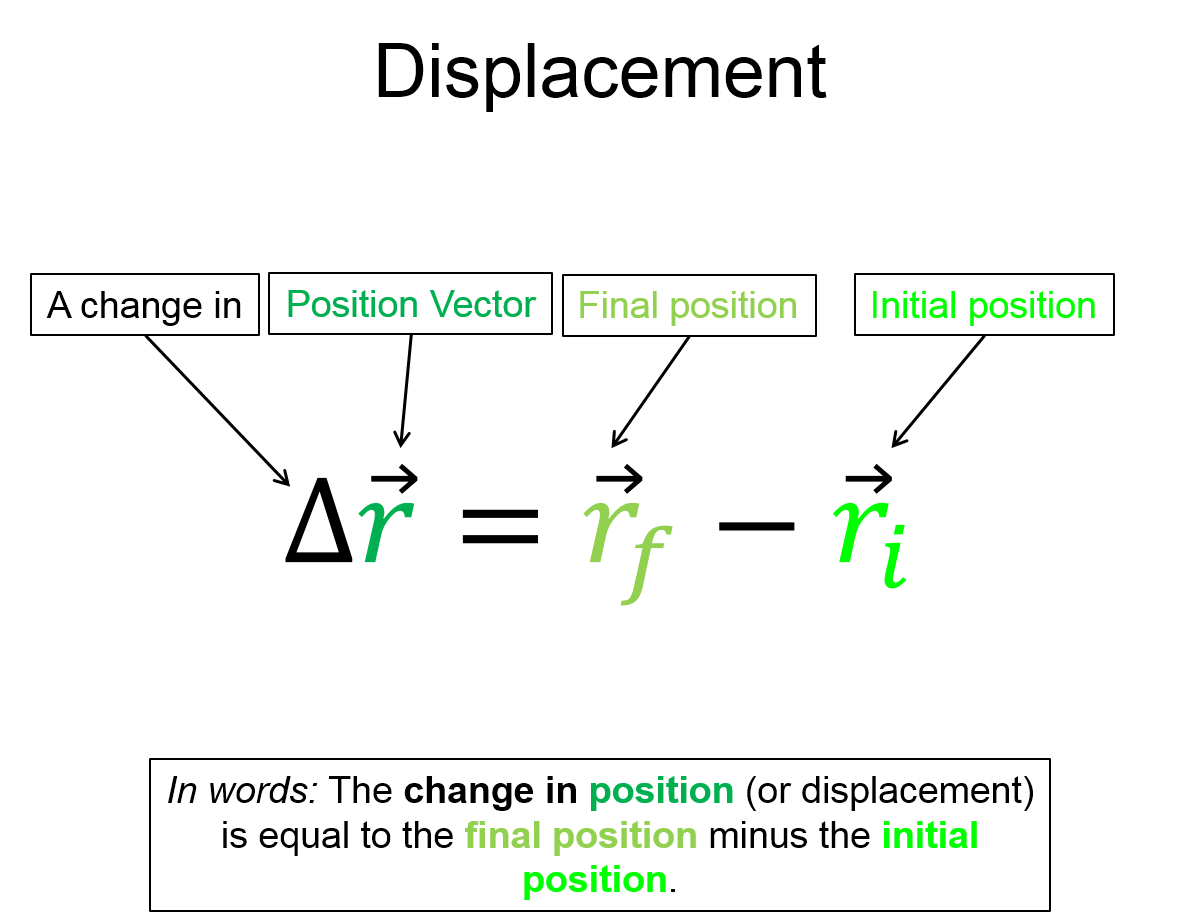
MR-VEC-1 Which of the following vector equations correctly describes the relationship among the vectors shown in the figure?

1. P + Q = R 

2. P = Q + R 

3. P + R = Q

4. P + Q + R =0

5. None of equations A - D is correct

MR-VEC-2 Start at the corner of a cube, of side length 1 m, and find the distance to the furthest point that still resides on the cube.

Note: the magnitude of a vector in three dimensions is the square root of the summation of the square of all three components of the vector.

Note: your answer should include units.

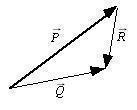
MR-VEC-3 You take off from La Guardia airport in a little airplane. First you fly NW for 5 miles. At the George Washington bridge, you turn SSW for 10 miles. Above the Statue of Liberty, you turn S toward the Verazzano Narrows bridge, 5 miles ahead. Over the bridge you turn ENE for a landing at JFK airport, 10 miles ahead.

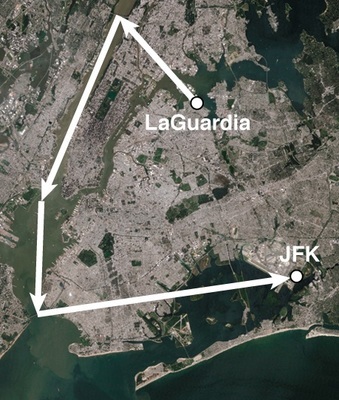
Suppose that instead of flying NW-SSW-S-ENE, you had followed the same "vectors" in a different sequence: SSW-NW-ENE-S. Mark on the map where this path would have led you.

MR-VEC-4 Three vectors, labeled P, Q, and R, are shown. The length of each vector is given in arbitrary units.

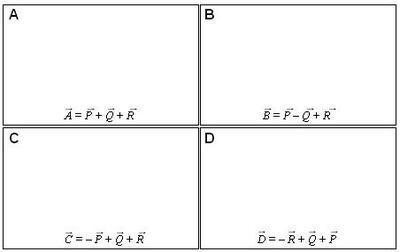
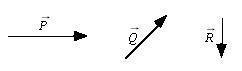
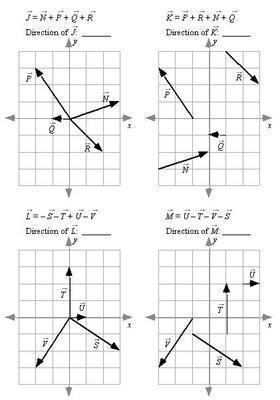
In each space provided above, construct a drawing of the indicated combinations of the vectors P, Q, and R, and then rank the magnitude of these resultant vectors.

MR-VEC-5 For each situation below, combine the vectors as indicated and determine the direction of the resultant vector. Then select the closest direction to the resultant from the direction rosette.

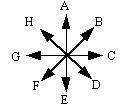
*** The questions from here down involve applying vector operations to positition, velocity, and acceleration ***

MR-VEC-6a Estimate the position vector to the location in the room defined as point A. Set the origin at the front, bottom, right side of the room (as seen by the students). Consider left to right as the positive x direction, bottom to top as positive y direction, and front to back as the positive z direction.

Answer in whole numbers of meters with the following format: <x,y,z> m. An example might look like: <4,1,7> m.

Estimate the position vector to the location in the room defined as point B.

Using the class average for position vectors A and B, find the displacement vector from point A to B. Answer in whole numbers of meters with the following format: <Δx,Δy,Δz>. An example might look like: <4,1,7> m.

MR-VEC-6b New Origin

  Estimate the position vector to the locations in the room defined as point A and point B.

This time set the origin at the front, top, left side of the room (as seen by the students). Consider left to right as the positive x direction, bottom to top as positive y direction, and front to back as the positive z direction.

Answer in whole numbers of meters with the following format: <xA,yA,zA> m, <xB,yB,zB> m. An example might look like: <4,1,7> m, <-2,3,6> m.

Using the class average for position vectors A and B from the new origin, find the displacement vector from point A to B.

Answer in whole numbers of meters with the following format: <Δx,Δy,Δz>. An example might look like: <4,1,7> m.

MR-VEC-7 Deserted on a deserted Island you spot a slightly exposed tin can under a tree. Upon opening it you find instructions to a buried treasure. It reads: “Ten paces from this very tree in a direction twenty degrees south of west lies the first location. Ten paces from this very tree in a direction sixty degrees north of east lies the second location. Walk from this tree exactly the distance and direction you would walk from the first location to the second location and you will find ye treasure. Yar” Sketch a physical representation of this situation on the grid provided. A physical representation for this type of problem should include the two position vectors, the change in the position vector, and the location of the treasure. Use the center of the grid as the tree location and scale appropriately to fit on the grid.

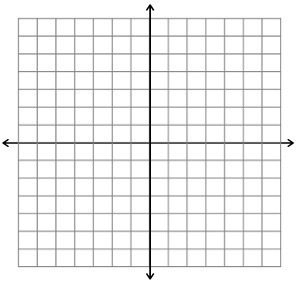
What are the coordinates of treasure?

MR-VEC-8 Upon waking from being hit in the head with a shovel you find yourself in the woods, next to a unfilled grave. You start running from this nightmare in a direction 51.34 degree from the negative y direction towards the negative x direction. Your acute direction senses surprise you but this is no time to contemplate a new super-power. You run along that line for 6.403 miles until you run into a police officer located at a location <-2, -3> miles from the police station. What are the coordinates of the grave you were presumably destined for?

1. <1, 8> mi

2. <4, -5> mi

3. <-2, 3> mi

4. <-1, -1> mi

5. <3, 1> mi