Entropy and the second law of thermodynamics are tough subjects to cover lightly. Entropy can be thought of as a measure of how much thermal energy per degree Kelvin is unavailable to do work. It is also a measure of disorder in a system. The second law of thermodynamics states that an isolated system will increase its entropy until it reaches equilibrium, where at that point the entropy is maximum and the system is the most disordered.
What is the 2nd law of thermodynamics? That question is answered by the Royal Institute.
Pre-lecture Study Resources
Watch the pre-lecture videos and read through the OpenStax text before doing the pre-lecture homework or attending class.
BoxSand Introduction
Thermo | Entropy and the 2nd Law of Thermodynamics
Though complex in its mathematics, entropy can be userstood from a conceptual level. To understand it we must talk about two related concepts, disorder and multiplicity. To explain these concepts imagine a container with two chambers that are seperated by a movable divider. The container will be our system and we can initiate the system by putting particles in either side. If I were to put 99 particles in the left side, and 1 in the right side, we would say that is a well ordered system (hold your questions). If the particles are identical you could exchange the single particle on the left with any one of the particles on the right. That means there are 99 different microscopic configurations that yield the same macroscopic state. We would consider that system of having a multiplicity of 99. Multiplicity is how many different ways you can rearrange the microcopic states (individual particles) to get the same overall macroscopic observable (99 on one side and 1 on the other). Entropy is a measure of this multiplicity.
Now if the divider is removed, and we picture these as particles of a gas, you would expect the system to not be in total equilibrium because some of the particles on the left would move to the right until there was about a 50/50 ratio - until there are about the same amount on each side. Now that the system is in equilibrium, what is the level of multiplicity? Well you can exchange one of the particles on the left with anyone of the 50 on the right, but can do that with anyone of the 50 particles on the left. That would be a multiplicity of 50x50 or 2500, it's actually much higher as we could talk about switching 2 or 3 or more at a time, but the point is the multiplicity increased as you moved from a state of non-equilibrium to a state of equilbrium.
So what about disorder? It's a tricky word but that's why I introduced the clearer word of multiplicity, because the original non-equilibrium state of the system was at a lower multiplicity, which also meant a more ordered state. More ordered in this sense meant there was only one particle at a time for me to change in the intial state and it would be much easier to keep track of the changes. In contrast, the high level of multiplicity in the equilibrium state makes it much harder to keep track of what changes can result in the same macroscopic 50/50 equilibrium state - there is a greater multiplicity. Thus we say the equilibrium state is less ordered. Since isolated systems drive towards equilbrium, they drive towards more disorder, a greater multiplicity, and a greater entropy.
The 2nd Law of Thermodynamics
The total entropy of an isolated system always increases over time until equilibrium is reached, wherein the entropy is maximum.
The second law of thermo, and the concept of entropy, are the only things in physics that have an arrow of time. They state that isolated systems go one way, but not the other. An example is in an isolated system, heat always flows from hot to cold and never the other way around (unless you put energy into the system, but then it is not isolated - think your refridgerator).
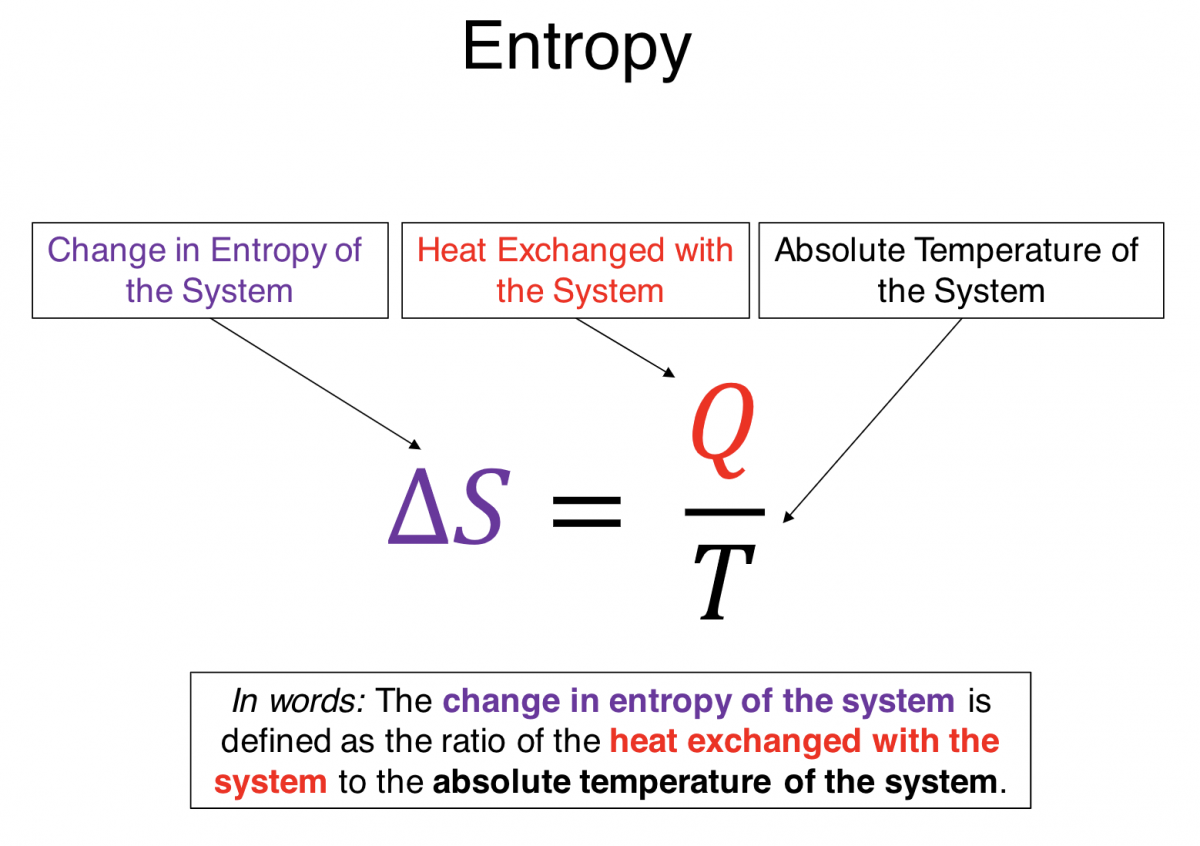
Entropy as it Relates to Heat: Normally I would not introduce an equation ($Q = \lim_{\Delta s \rightarrow 0} \sum T \Delta s$) beyond the scope of this discussion, but in this case I want you see that heat (Q) is related to a change in entropy ($\Delta s$). If the heat transfer of your system is positive, which equates to energy entering your system, so is the change in entropy of the system. When the divider from the example above is removed, convection causes the particles to flow from the left to the right side. This results in a heat transfer and thus an increase in entropy. Perhaps a more concrete example is to consider a cube of ice melting. Energy is entering the system during the phase transition but the temperature does not change. The entropy of the ice is increasing because the heat is positive, but that heat energy is going into breaking the bonds and changing the configurational state of the system. And what about order? A solid with a well ordered crystalline lattice, is more ordered than the random motion of molecules rolling around each other, like in the case of a liquid.
Note that none of this discussion is impendent on temperature. If the particles on both sides of the chamber had the same average kinetic energy, the system was in thermal equilibrium, but it was not in total equilbrium because of the configurational change that entropy drives. This is why entropy is sometimes refered to configurational energy that is not available to do work, it's simply bound up in setting the most multiplicitive state possible.
Key Equations and Infographics
Now, take a look at the pre-lecture reading and videos below.
BoxSand Videos
Required Videos
Suggested Supplemental Videos
OpenStax Reading
OpenStax Section 15.6 | Entropy and the Second Law of Thermodynamics: Disorder and the Unavailability of Energy
OpenStax Section 15.7 | Statistical Interpretation of Entropy and the Second Law of Thermodynamics: The Underlying Explanation
Fundamental examples
1. (a) You have three white marbles and four boxes in a line. Each box can hold only one marble. How many unique ways can you put marbles in boxes in this system (i.e. what is the multiplicity of the system)? (b) Now you have two white marbles, a red marble, and four boxes. What is the multiplicity of the system? Which system has a higher entropy, that described in (a) or in (b)?
2. A red-hot brick of lead is thrown into a bucket of water. Which of the following statements are true?
(a) The entropy of the lead decreased while the entropy of the water increased.
(b) The entropy of the water decreased while the entropy of the steam increased.
(c) The entropy of the steam decreased while the entropy of the water increased.
(d) The water gained more entropy than the lead lost.
(e) The lead gained more entropy than the water lost.
3. During a thermodynamic process, 2 kJ of work is done on a gas and the thermal energy increased by 300 J. (a) Was the change in entropy of the system positive or negative? (b) If, in part (a), the entropy change was negative, how is this possible (how would this not violate the second law of thermodynamics)?
Short foundation building questions, often used as clicker questions, can be found in the clicker questions repository for this subject.
Post-Lecture Study Resources
Use the supplemental resources below to support your post-lecture study.
Practice Problems
BoxSand's multiple select problems
BoxSand's quantitative problems
Recommended example practice problems
For additional practice problems and worked examples, visit the link below. If you've found example problems that you've used please help us out and submit them to the student contributed content section.
Additional Boxsand Study Resources
Additional BoxSand Study Resources
Learning Objectives
Summary
Summary
Atomistic Goals
Students will be able to...
YouTube Videos
Awesome conceptual video that looks at the big picture.
A good video lecture explaining entropy, the second law with a few problems.
Doc Schuster explains the second law of thermodynamics
Doc Schuster Explains Entropy, Disorder, and the Eventual Heat Death of the universe.
Other Resources
This link will take you to the repository of other content related resources .
Simulations
The concept of reversible reactions is about entropy.
For additional simulations on this subject, visit the simulations repository.
Demos
History
Oh no, we haven't been able to write up a history overview for this topic. If you'd like to contribute, contact the director of BoxSand, KC Walsh (walshke@oregonstate.edu).
Physics Fun
Other Resources
Hyperphysics page on Entropy and the Second Law of Thermodynamics. We will go into heat cycles more in an upcoming section.
Boundless section on entropy and the second law,
Boston University's reference page on entropy and the second law.
Resource Repository
This link will take you to the repository of other content related resources .
Problem Solving Guide
Use the Tips and Tricks below to support your post-lecture study.
Assumptions
The 2nd law of Thermodynamics says that for an isolated system, entropy can only increase or remain the same, but never decrease. However, the subtly here lies in the words "isolated system". What is an isolated system? In thermodynamics, it means a system for which no heat or work can leave or enter the system from external elements. This can be applied to systems that are far away from other systems or even to the entire universe (since no well verified theory currently says our universe interacts with systems outside itself). In everyday life, a isolated system could be approximated by any system surrounded by Styrofoam or even a blanket that would insulate it from heat transfer with the outside enviroment.
This becomes important when we think about the 2nd law because it is possible for a system's entropy to decrease! It can happen if the system transfer heat out to an external system (losing heat usually means losing entropy) and that external system increases its entropy as much or more than our system lost its entropy. The "as much or more" accounts for the inequality in the 2nd law, because it is possible for the entropy total of both systems to have increased, even if one of our system's entropy decreased! Do not fall into the trap of thinking that entropy will only ever increase, in special cases it can decrease for individual non-isolated system.
In a sense, entropy works like energy does, in the sense that it can transfer between systems (usually through heat, which is a type of energy!). However, where energy cannot be created or destroyed, it is the natural tendency of the universe to actively create entropy as systems interact! Entropy cannot be destroyed, for it to decrease in a system, it must simply go someplace else. However, the 2nd law tells us the universe spontaneously creates entropy, and never truly destroys it! So what happens as we get more and more entropy, and never lose any? -> https://en.wikipedia.org/wiki/Heat_death_of_the_universe
Misconceptions & Mistakes
- If you are a chemist, you may be thinking about changes in Gibbs free energy, which is the change of energy of a system in terms of its enthalpy (heat) and entropy. Be careful: while they are closely related, our definition of internal energy and Gibbs free energy are NOT identical equations.
Pro Tips
- Counting is one of the hardest parts of physics (ask any grad student). Take your time with it and use a full sheet of paper each time you are trying to find the multiplicity of a system (see solutions to Fundamental problem #1 for an example).
- Memorize that $\Delta S \space \alpha \space Q$. This is a hard thing to reason out using logic or intuition or the physical tools you have available, and is a very useful fact to have at the front of your mind.
- If you have some chemistry background, do not just tune out. You need to practice these problems from a physicists perspective. The chemistry background will help you but I guarantee you will have a bad grade in this section if you relax your study habits thinking you already know some of the content.
Multiple Representations
Multiple Representations is the concept that a physical phenomena can be expressed in different ways.
Physical
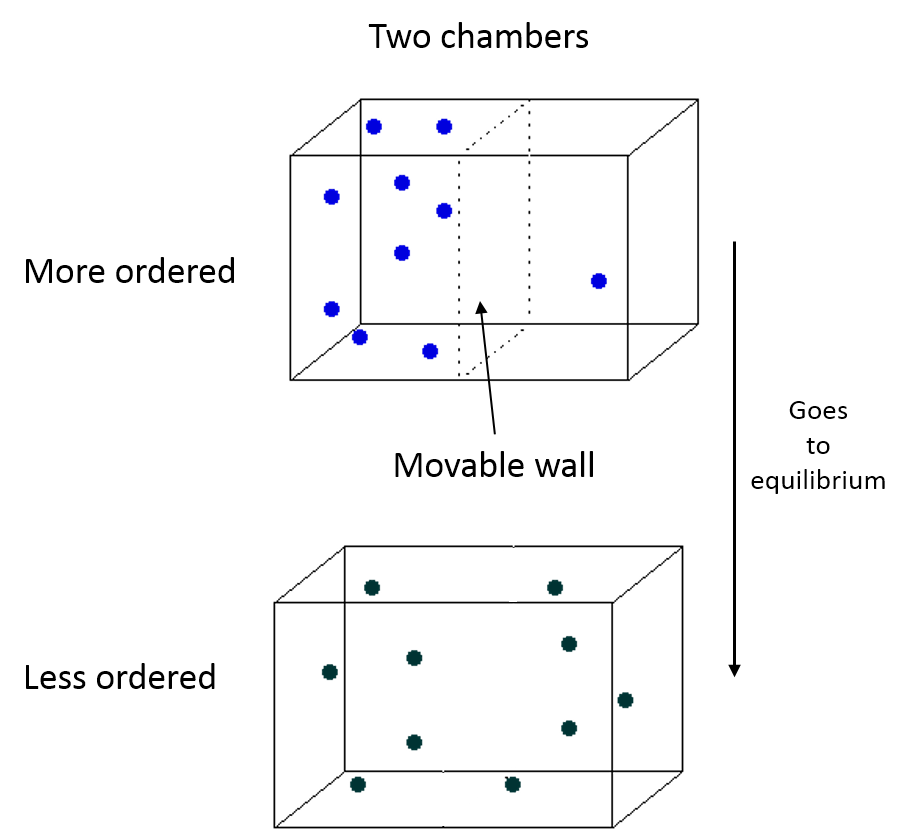
We have a system with a moveable wall. Once the wall is removed, the particles move toward a new equilibrium.
Mathematical
$*Q = \lim_{\Delta S \to 0} \sum T \Delta S $
*Actual equation not important.What is important is that conceptually heat is proportional to the change in entropy.
Conceptually, heat (Q) is from $\Delta S$
Graphical
Descriptive
Entropy drives isolated systems, such as the boxes of particles shown in the Physical Representation, to increased disorder. Where more disorder has larger micro multiplicity and a larger multiplicity means more microscopic configurations with the same macroscopic observables such temperature (T), pressure (P), $E_{th}$, etc...
Experimental
We can design an experiment by taking a water filled ballon and popping it. Initially, the water in the balloon is contained and relatively uniform. However, as soon as we pop the balloon the water molecules become scattered and begin to spread out to form a new equilibrium.