Spiders ride electric fields to fly hundreds of miles.
Pre-lecture Study Resources
Watch the pre-lecture videos and read through the OpenStax text before doing the pre-lecture homework or attending class.
BoxSand Introduction
Electric Fields | Field Model and Charges in an Electric Field
Field Theory
A field is a map. It tells you how navigating a region of space may go before you even get there. Imagine a room being warmed by a fireplace in the corner. I could walk to every point in the room, staring with position $\overrightarrow{r}=<0,0,0> m$, and record the temperature in a data table. That table represents the temperature field of the room. That scalar field could then be used to deduce heat transfers in the room. Fields are maps, where every point in space there is information (usually a scalar or a vector), that can be used to explain interactions. Fields are constructs, more than any other we've encountered. They are not observable in any conventional way but are rather a conceptual tool for the study of interactions.
An example of a vector field is a velocity field. Instead of every point in space containing one number, like in the temperature field example, every point in space contains three numbers which are the x, y, and z components of the velocity. A stream that narrows could possibly be described by the velocity field below.
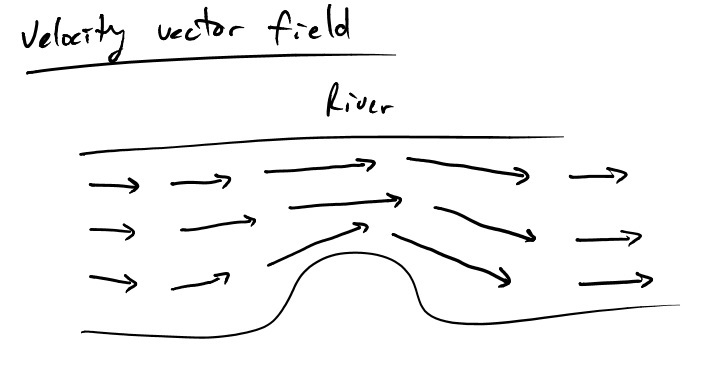
Even though there are not vectors drawn everywhere in the stream does not mean the field is zero at those points, its merely due to the limitation of how many vectors are feasible (and useful) to draw. Now a rubber ducky floating down the river could have a somewhat predictable interaction with the river. It would speed up in the narrow region and possibly change directions if it entered from the bottom. Be careful, the temperature and velocity field examples are not the same as the electric field and potential. They are only used to get a loose feel for the concept.
The Electric Field
All charges create electric fields. We say the charge alters the space around it but this not true in any real way, that is what mass does. Charges rather create a field that can travel through the vacuum of space and influence other charges to feel a force. Consider the situation below where $Q$ is a positive charge that generates the vector field shown. That is the field owned by charge $Q$.
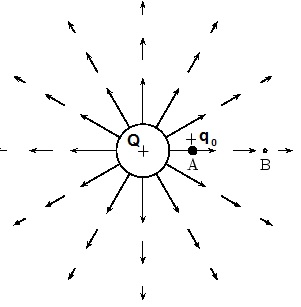
A second charge $q_0$, whose field is not being shown, resides in $Q's$ field. We call $q_0$ the test charge since we are not considering the field it creates. If the electric field from $Q$ is considered to be $\overrightarrow{E}$, then the force that field puts on the test charge follows the following equation.
Force on a Test Charge ($q_0$) in an Electric Field ($\overrightarrow{E}$)
$\overrightarrow{F_0}=q_0 \overrightarrow{E}$
The essence of an electric field lies in this example. The charge $Q$ generates a field that a second charge $q_0$ feels a force from and in that way they interact. This model gives $Q$ ownership to something that can exist without the presence of the second charge. After all, there would be no such thing as a Coulomb force if the second charge didn't exist. It is this reason some consider the electric field to be more fundamental and elegant than Coulombs Law.
Key Equations and Infographics
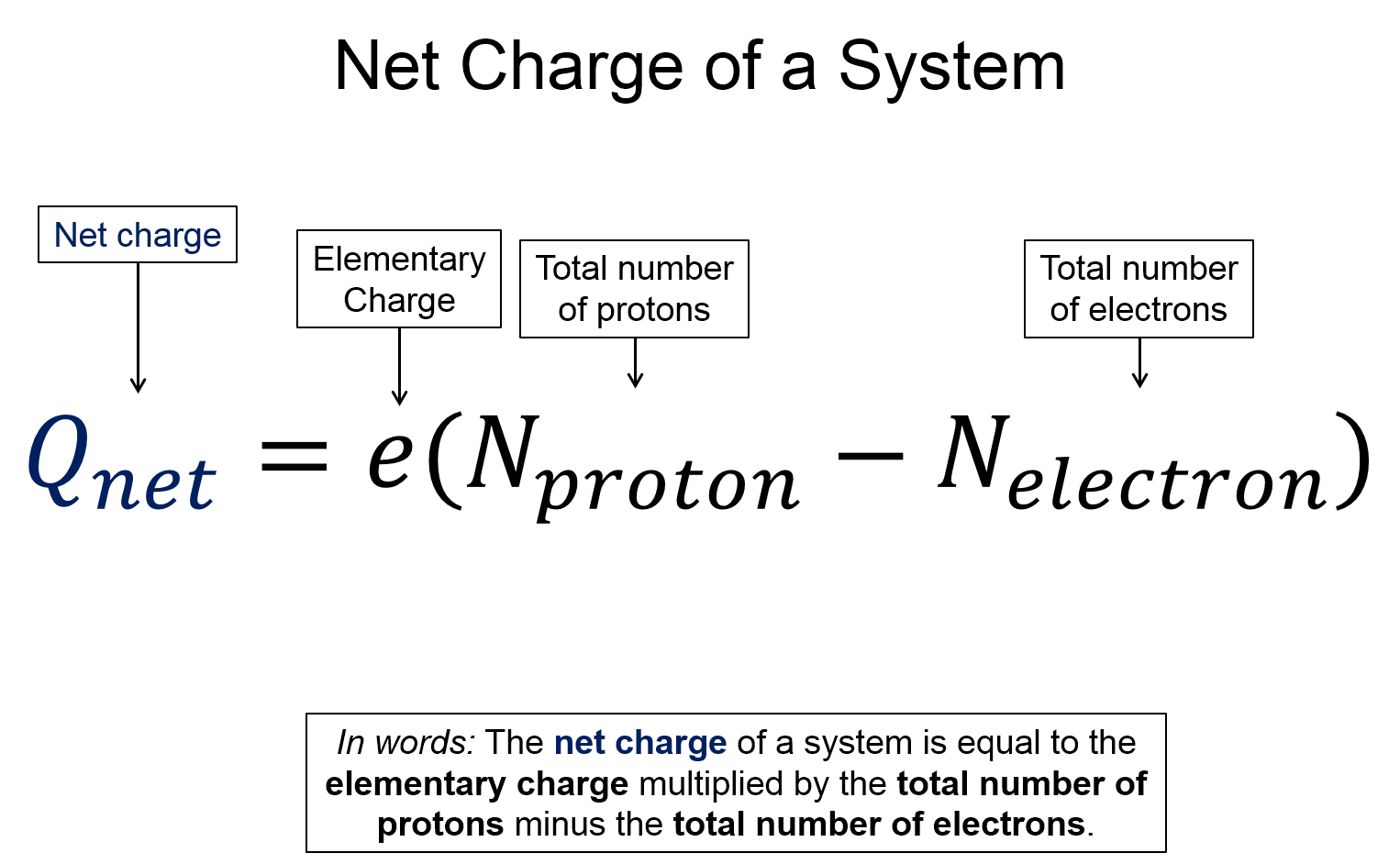



Now, take a look at the pre-lecture reading and videos below.
BoxSand Videos
OpenStax Reading
Fundamental examples
(1) A point charge with charge $q_1 = 1.8 nC$ is located at the origin. A point charge with charge $q_2 = 3.6 nC$ is located a distance $r_{12} = 6 nm$ away. (a) What is the magnitude of the coulomb force from charge 1 on charge 2? (b) Is this an attractive or repulsive force?
(2) A point charge with charge $q_1 = - 1.8 nC$ is located at the origin. A point charge with charge $q_2 = 3.6 nC$ is located a distance $r_{12} = 6 nm$ away. What is the magnitude of the coulomb force from charge 1 on charge 2?
(3) A point charge with charge $q_1 = - 1.8 nC$ is located at the origin. A point charge with charge $q_2 = 3.6 nC$ is located a distance $r_{12} = 6 nm$ away. A point charge with charge $q_3 = 5 nC$ is located at a position $r_3 = <2,2> nm$. What is the magnitude of the coulomb force from charge 1 on charge 2?
Solutions found HERE
Short foundation building questions, often used as clicker questions, can be found in the clicker questions repository for this subject.
Post-Lecture Study Resources
Use the supplemental resources below to support your post-lecture study.
Practice Problems
BoxSand practice problems - Answers
BoxSand's multiple select problems
BoxSand's quantitative problems
Recommended example practice problems
- OpenStax, Period and Frequency also linked in Charges & the Electric Force sections.
- Static Electricity and Charge, Website Link
- Conductors and Insulators, Website Link
- Coulomb's Law, Website Link
- Large set of questions on electric charge and force. External PDF
- Coulomb's Law Review, External PDF
For additional practice problems and worked examples, visit the link below. If you've found example problems that you've used please help us out and submit them to the student contributed content section.
Additional Boxsand Study Resources
Additional BoxSand Study Resources
Learning Objectives
Summary
Summary
Atomistic Goals
Students will be able to...
YouTube Videos
Pre-Med Academy is back with three well put together videos on our main subjects, Electric Charge, Electric Force, and Coulomb's Law
Youtube: Pre-Med Academy - Coulomb's Law
Step By Step Science has several example problems, here are a few on using Coulomb's Law. There are more in this section's content repository.
Other Resources
This link will take you to the repository of other content related resources .
Simulations
This simulation by Duffy helps you with Coulombs Law and Newton's 2nd law
The colorado PhET simulation is everything you ever needed in life, that you didn't know that you needed. We present to you, John Travoltage.
Charge transfer PhET simulation with baloons and a sweater.
For additional simulations on this subject, visit the simulations repository.
Demos
Rub a plastic cup against carpet, hair, or fur, and observe the effects of the net charge now on the cup.

For additional demos involving this subject, visit the demo repository
History
Oh no, we haven't been able to write up a history overview for this topic. If you'd like to contribute, contact the director of BoxSand, KC Walsh (walshke@oregonstate.edu).
Physics Fun
Surface tension is a polarization force between atoms. It's responsible for holding a water droplet together.

Play with John Travolta's leg and arm to get a Travoltage.
Other Resources
Resource Repository
Use the supplemental resources below to support your post-lecture study.
Boston University's Page on electric charge and Coulomb's law is neat reference with a couple of example problems
PPLATO is a complete resource with a lot of information, and several practice questions per subject. This webpage covers electric charge, the electric field, and electric potential, frocus on the electric charge, we'll get back around to field and potential later.
The Hyperphysics and their reference card for Coulomb's Law and the electric force.
The Physics Classroom has an entire chapter on static electricity. The last lesson of the chapter is on Electric Fields so save that for later!
Problem Solving Guide
Use the Tips and Tricks below to support your post-lecture study.
Assumptions
Checklist
Misconceptions & Mistakes
- If you have two charges QQ and qq, and the magnitude of charge QQ is greater than that of charge qq, the two charges still apply an equal and opposite force to each other. Regardless of the relative magnitudes, Newton's 3rd Law still holds.
- While you can induce a dipole in both insulators and conductors, the atomic nature of the dipole is different for the two cases.
Pro Tips
Multiple Representations
Multiple Representations is the concept that a physical phenomena can be expressed in different ways.
Physical
Mathematical
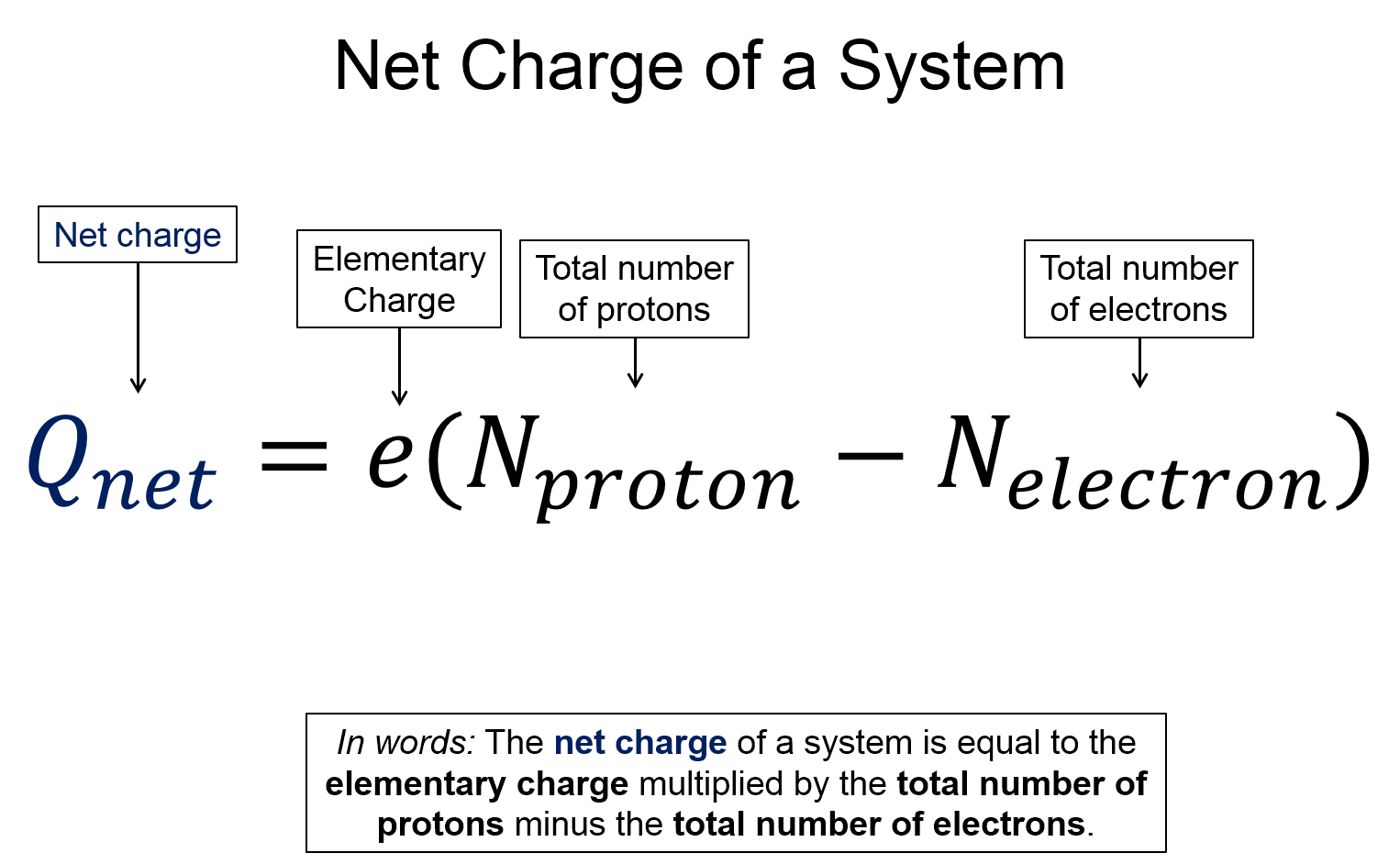



Graphical
Descriptive
Experimental
