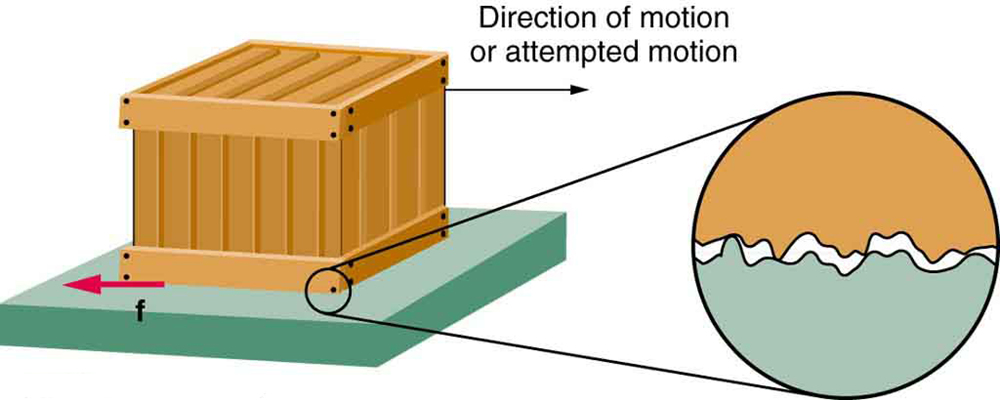
Friction arises when two surfaces are in contact with each other and are pushed in a way that makes the surfaces want to slide relative to each other. Note they don't have to be sliding. Air resistance is also a form of friction.
This concept trailer from OpenStax talks about drag.
Pre-lecture Study Resources
Read the BoxSand Introduction and watch the pre-lecture videos before doing the pre-lecture homework or attending class. If you have time, or would like more preparation, please read the OpenStax textbook and/or try the fundamental examples provided below.
BoxSand Introduction
Newton's Laws 2 | Friction
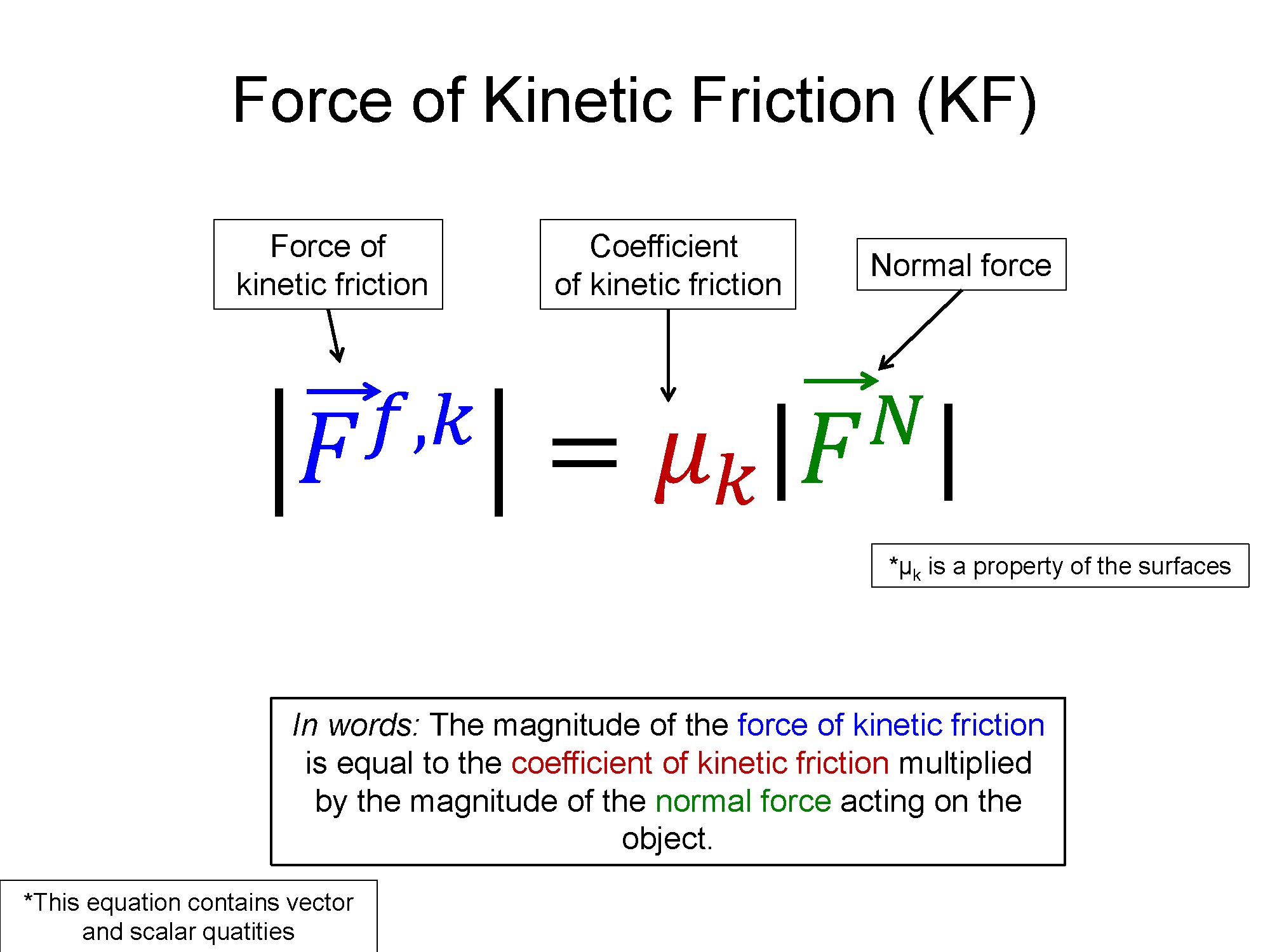
Friction is a force that arises between two objects that have surfaces in contact with one another. Friction opposes the relative motion between two objects, if they are slipping, and opposes the direction they would slip if the friction was not present, for those that are not slipping. Friction comes in two types, static friction and kinetic friction. Kinetic friction acts when the surfaces of the objects are slipping. It is equal in magnitude to the normal force at the surface times the coefficient of kinetic friction. Static friction acts when there is no relative motion between the objects. The force of static friction is as large as it needs to be to prevent the objects from slipping. The maximum force of static friction is equal to the normal force at the surface times the coefficient of static friction.
Key Equations and Infographics


Now, take a look at the pre-lecture reading and videos below.
BoxSand Videos
Required Videos
Suggested Supplemental Videos
OpenStax Reading
Fundamental examples
1.) What is the direction of the frictional force on the block?

2.) The car in the image below is accelerating to the right and the block is not sliding with respect to the car. What is the direction of the frictional force on the block from the car?

(a) To the left (b) To the right (c) Not enough information.
3.) A block with mass $M = 5 \, kg$ rests on a surface with a coefficient of static friction of $\mu_s=0.5$ and a coefficient of kinetic friction of $\mu_k=0.3$. A force is applied pushing it to the right.

(a) What is the max force that can be applied to have the block remain stationary?
(b) What happens if half the max force, from (a), is applied to the block?
(c) The block is traveling to the right with a magnitude of the applied force, $| \vec{F}^{A}|=20N$, what is
the acceleration of the block?
CLICK HERE for solutions.
Short foundation building questions, often used as clicker questions, can be found in the clicker questions repository for this subject.
Post-Lecture Study Resources
Use the supplemental resources below to support your post-lecture study.
Practice Problems
BoxSand's Quantitative Practice Problems
BoxSand's Multiple Select Problems
PDF's
BoxSand Practice Problems (SOLUTIONS)
Links
Recommended example practice problems
Set 1: 4 problems with very clear solutions
Set 2: 8 problems with visuals and solutions
Set 3: Problems 11, 12, 15, 16, 18, 23, 24, 26, 27,
For additional practice problems and worked examples, visit the link below. If you've found example problems that you've used please help us out and submit them to the student contributed content section.
Additional Boxsand Study Resources
Additional BoxSand Study Resources
YouTube Videos
Simulations
This applet has some great tools to learn about friction. Near the top of the applet there is a tab that says friction; open that. Start by just applying a small force. Watch what happens to the force of friction as you increase the applied force? What happens when the applied force gets very big? After static friction is broken what can we say about the magnitude of the force of friction as the block slides around?
(download)
Now try the same thing, but with a ramp;
(download)
For additional simulations on this subject, visit the simulations repository.
Demos
History
Oh no, we haven't been able to write up a history overview for this topic. If you'd like to contribute, contact the director of BoxSand, KC Walsh (walshke@oregonstate.edu).
Physics Fun
Oh no, we haven't been able to post any fun stuff for this topic yet. If you have any fun physics videos or webpages for this topic, send them to the director of BoxSand, KC Walsh (walshke@oregonstate.edu).
Other Resources
Warning: Be aware that HyperPhysics doesn't always indicate the vector nature of certain quantities and expects the reader to know from context if something is a vector. Remember, forces always have a magnitude AND direction and must always be added using vectors.
Here' s a link to HyprerPhysics's page about Friction:
Resource Repository
This link will take you to the repository of other content on this topic.
Learning Objectives
Summary
We will learn about the features of the frictional force. Additionally it presents a unique situation where a vector in one direction (normal force) is perpendicular to a vector in another direction (friction) but the magnitude of the normal force affects the magnitude of the friction. Inclined planes are a physical situation where student must wrestle with a non-traditional coordinate system and the vector components in that system.
Atomistic Goals
Students will be able to...
- Recognize that friction is an interaction between surfaces and therefore depends on both materials.
- Demonstrate that if two objects are not sliding relative to each other, than the static friction force is as large as it needs to be, up to a maximum value.
- Demonstrate that if two objects are sliding relative to each other, then the kinetic friction force is constant.
- Show how the magnitude of the friction force is related to the magnitude of the normal force, via the coefficient of friction; always true for kinetic friction and only true for static friction when it's a maximum.
- Identify the mechanisms that go into rolling friction and how the magnitude depends on the normal force.
- Identify a system where rolling friction is present and not negligible.
- Show that the friction force is parallel to a surface.
- (UPMF) Demonstrate that the direction of the friction force is opposite the direction of relative motion (or what relative motion would occur without friction) between two surfaces.
- (UPMF) Demonstrate that if friction is the only force acting in a given direction, then it must be in the same direction as the acceleration component in that direction.
- Use multiple approaches to make sense of the direction of friction, e.g. connecting the FBD to the direction of the net force and acceleration.
- Identify other forces related to friction, including air resistance, viscosity, and cohesion.
- Recognize when friction can safely be neglected.
Problem Solving Guide
Use the Tips and Tricks below to support your post-lecture study.
Assumptions
- Friction is a force that opposes motion. If kinetic friction is present, it will act in the opposite direction of motion and try to slow it down. If static friction is present, it will point in the direction that causes the system to not move. Think about the forces or velocities that instigate or attempt to instigate motion of an object and what friction would need to do to oppose them in your free body diagrams!
- Friction is dependent on the presence of normal force, they are directly proportional in magnitude, so if the normal force disappears, the friction force does as well. However, normal force and friction force, by definition, point in perpendicular directions. Normal force points perpendicular (directly away) from a surface and friction points tangentially along it. Remember that this 90 degree difference must always be true and usually gives a convenient set of axes for you to use for your sum of forces.
Checklist
Misconceptions & Mistakes
- Oftentimes in physics the angle given is not the angle you need to use in the problem. Do not assume, check the angle is correct, especially on exams.
- Position and velocity have no bearing on acceleration, which takes its cues from forces on the system. Forces tell objects how to accelerate, acceleration tells velocity how to change, velocity tells position how to change. Acceleration is the ultimate root of motion, brought about by force interactions.
Pro Tips
- For free body diagrams, first find the normal force and gravity, those tend to be the easiest to pin down. From there, you know firction is 90 degrees off of normal force, so you only have 2 choices in a 2D problem. Sometimes you may not know the direction of friction and will need to make an assumption. This is fine. Chose an artbitrary direction and if a quantity you're solving for comes out a different sign than you expect through your sensemaking, you probably made the wrong choice, but this is an easy fix (flip the sign and do the math again). The trick is to not get caught up, making assumptions and trying a problem one way and finding out it was wrong only to fix it and get it right the second time, is still getting the right answer and is truly science at work!
- Some situations will not directly tell you if static friction is overcome or not, and will give you kinetic friction and static friction consants. In this case, calculate the static friction, and see if it is bigger or less than the force attempting to move the object. If it is, the object will stay put. If it is smaller, the object will move and now you know you need to analyze the motion using kinetic friciton in your free body diagram!
Multiple Representations
Multiple Representations is the concept that a physical phenomena can be expressed in different ways.
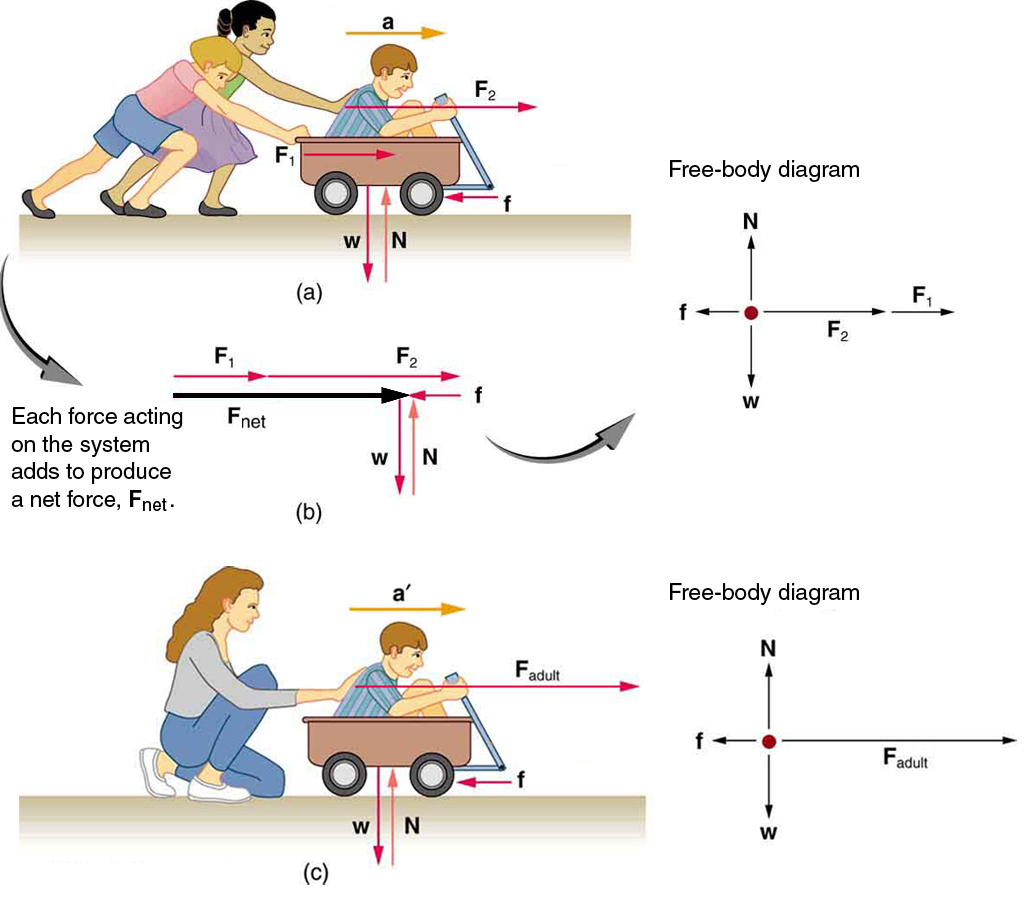
Physical
Mathematical
The main mathematical representation for forces will be applying Newton's Second Law to a physical problem. You will need to analyze the motion of an object and create a free body diagram of the relative forces in order to derive the force equations. We learned in the kinematics section how to analyze motion without any concern about the forces that caused the motion. The infographic below describes the relationship between force and acceleration. Thus, we may now analyze the forces acting on an object to determine the relative acceleration.

Graphical
 .
.
Descriptive
A spaceship, deep in space, has ran out of fuel. Since nothing is there to act on the ship, it will continue to move at the speed it is moving and in the direction it is moving. It will do this until something acts on it, something like the pull from a nearby star that becomes no longer negligible as the ship passes near the star.
Experimental