Often times an object we are trying to analyze with FBDs sits atop a surface that is not parallel to the ground. This slight variation adds some noteworthy complexities that we will cover in this section.
Inclined planes can be used for mechanical advantage. It is considered a Simple Machine.
Pre-lecture Study Resources
Read the BoxSand Introduction and watch the pre-lecture videos before doing the pre-lecture homework or attending class. If you have time, or would like more preparation, please read the OpenStax textbook and/or try the fundamental examples provided below.
BoxSand Introduction
Forces | Inclined Planes
Objects on a non-horizontal surface are considered to be on an inclined plane. If they slide up or down the incline their acceleration is not horizontal. Some forces acting on the object, with the normal force being an example, are off at an angle and not straight vertical (or horizontal). This presents a unique example of a system where rotating your coordinate system is beneficial to the analysis. Consider the block below and think about the direction of forces acting on it. Using a standard horizontal and vertical coordinate system (not pictured), you would have to break the tension and normal force into components. Furthermore, If the block was accelerating, without flying off the incline or falling through it, the block's acceleration would be along the incline, off at an angle from the horizontal. The acceleration would also have to be broken into components. To illustrate how cumbersome this choice of coordinate system makes the calculation, consider the case where the hanging mass is not large enough to hold the block and it is accelerating down the incline. Newton's 2nd law would look as follows with a standard positive x to the right and positive y upward. Note: the open resource diagram below doesn't use the letter F for all the forces like we encourage you do.
$\sum\overrightarrow{F}= m \overrightarrow{a} \rightarrow$ $\langle T\cos{\alpha}-N\cos{\alpha}, T\sin{\alpha}+N\sin{\alpha}-F_g\rangle = m \langle -a\cos{\alpha},-a\sin{\alpha} \rangle$
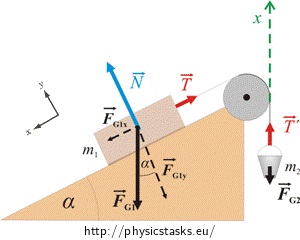
What if instead of using a horizontal and vertical coordinate system you were to define one where the positive x direction pointed parallel to the incline, as shown in the figure. Now the tension and the normal force, are 100% in the x direction. Movement along the incline will now be along the x direction and so will the any acceleration. The only thing then that needs to be broken into components is the force of gravity. Newton's 2nd law is reduced to the following.
$\sum \overrightarrow{F} = m \overrightarrow{a} \rightarrow$ $\langle F_g\sin{\alpha}-T, N-F_g\cos{\alpha}\rangle = m \langle a,0 \rangle$
The algebra and arithmetic will be much easier using a rotated coordinate system. The biggest issue it to figure out what the new x and y components are for a rotated system. Watch my lecture video for a technique to get the components correct in a rotated coordinate system. Once you've done it a few times, I believe you'll agree the work to learn how to rotate the coordinate system is worth the savings in algebra headaches of not rotating your coordinate system. If you're still not convinced, imagine having to then do kinematics problems with the acceleration you have just calculated doing a force analysis. With a standard coordinate system it is a 2D problem and you'll have a set of kinematic equations for both the x and y directions. With a rotated coordinate system, assuming the object doesn't leave the incline, the velocity, acceleration, and change in position are zero in the direction perpendicular to the plane, making it a 1D problem.
Here's a short video to visualize the components of gravitational force (they use the letter P), and the normal force (N).
Key Equations and Infographics
Now, take a look at the pre-lecture reading and videos below.
BoxSand Videos
Required Videos
Snakes on an Inclined Plane - No Friction - (12 min)
Previous Screen Capture Video
Suggested Supplemental Videos
OpenStax Reading
Fundamental examples
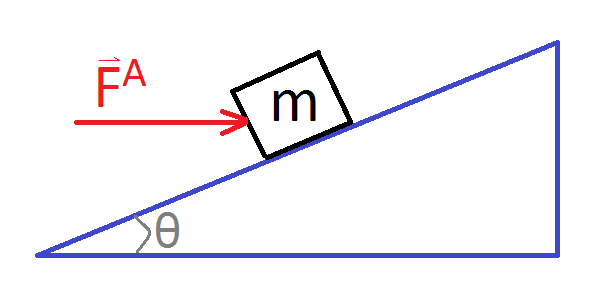
1. Consider consider a $1.5 \, kg$ object on a frictionless incline as shown in the image below. If the magnitude of $\vec{F}^A$ is equal to $8 \, N$ and the angled labeled is $60^{\circ}$, what is the acceleration of the object?
2. Lombard Street in San Francisco, uses a curvy road to help mitigate the steep hill that cars must travel down. If approximated as an incline plane, Lombard Street roughly makes a $27^{\circ}$ incline with respect to the horizontal.
a) Find the force of static friction if the coefficient of static ($\mu_s$) friction between Lombard Street and a car's tires is $0.70$. The car has a mass of $1381 \, kg$.
b) What is the minimum value that $\mu_s$ can be before your car starts to slip down the street?
CLICK HERE for solutions.
Short foundation building questions, often used as clicker questions, can be found in the clicker questions repository for this subject.
Post-Lecture Study Resources
Use the supplemental resources below to support your post-lecture study.
Practice Problems
BoxSand's Quantitative Practice Problems
BoxSand's Multiple Select Problems
Recommended example practice problems
Solutions to BoxSand Practice Problems
Set 1: Normal Forces interactive set/quiz
Set 2: Sled, Sled 2: The Friction Strikes Back, Mountain Road
For additional practice problems and worked examples, visit the link below. If you've found example problems that you've used please help us out and submit them to the student contributed content section.
For additional practice problems and worked examples, visit the link below. If you've found example problems that you've used please help us out and submit them to the student contributed content section.
Additional Boxsand Study Resources
Additional BoxSand Study Resources
Learning Objectives
Summary
Inclined planes are a physical situation where students must wrestle with a non-traditional coordinate system and the vector components in that system.
Atomistic Goals
Students will be able to...
- Identify the direction of acceleration and weigh the value of aligning your coordinate system with that direction as opposed to choosing one that minimizes the number of force components.
- Orient the forces in a FBD in the direction they are applied and not rotated to align with a horizontal or vertical direction.
- Translate a given angle in the physical representation to all like angles in a FBD, which may require geometry.
Additional Study Resources
Use the supplemental resources below to support your post-lecture study.
YouTube Videos
Khan Academy explains inclined plan force components you may see when solving inclined plane problems:
This is a simple introduction to motion on an inclined plane with no friction:
Doc Schuster describes techniques for solving inclined plane problems
This a short video lecture by APlusPhysics on Ramp and Inclines;
Simulations
This phet simulation highlights the physics when working with inclined planes.
For additional simulations on this subject, visit the simulations repository.
Demos
History
Oh no, we haven't been able to write up a history overview for this topic. If you'd like to contribute, contact the director of BoxSand, KC Walsh (walshke@oregonstate.edu).
Physics Fun
Oh no, we haven't been able to post any fun stuff for this topic yet. If you have any fun physics videos or webpages for this topic, send them to the director of BoxSand, KC Walsh (walshke@oregonstate.edu).
Other Resources
Physics Classroom: Inclined planes
In addition to the textbook above be sure to read the EasyPhysics Inclined Plane with Gravity section which describes decomposed forces on an inclined plane a little differently.
Resource Repository
This link will take you to the repository of other content on this topic.
Problem Solving Guide
Use the Tips and Tricks below to support your post-lecture study.
Assumptions
Remember that inclined plane problems are just tilted standard problems, so the same rules apply, i.e. draw a FBD, sum forces, set equal to ma, solve for forces/acceleration and analyze motion.
In these problems, it is often useful to align your axes with your inclined plane, this will result in the normal force and friction force (if any) will be on axis, but gravitational force and other forces will often need to be decomposed into vectors that point along our new axes.
Checklist
Misconceptions & Mistakes
- Oftentimes in physics the angle given is not the angle you need to use in the problem. Do not assume, check the angle is correct, especially on exams.
- Position and velocity have no bearing on acceleration, which takes its cues from forces on the system. Forces tell objects how to accelerate, acceleration tells velocity how to change, velocity tells position how to change. Acceleration is the ultimate root of motion, brought about by force interactions.
Pro Tips
- Remember that all equations you can derive on an inclined plane should reduce to a flat plane if you set the angle of the plan to 0. Oftentimes they will also reduce to free fall if you set the angle of the plane to 90 degrees we well! Use these types of checks to see if your equations make sense!.
- Often one of the most challenging parts of an inclined plane is translating the angle given into your equations. One of the best ways to make this easier is to find the angle of the incline as it relates to one of your vectors, then draw a traditional horizontal axis and a vertical axis. Then, draw axes that align with your inclined plan, one along the inclined plane and normal (pointing directly perpendicular) to it. Now, using these two sets of lines, you can say that every OTHER angle between those lines is the same (so only 2 unique angles are found between the lines). You can easily fill in the angles from there after knowing only 1. This is known as the pizza wedge tick, take a look below:
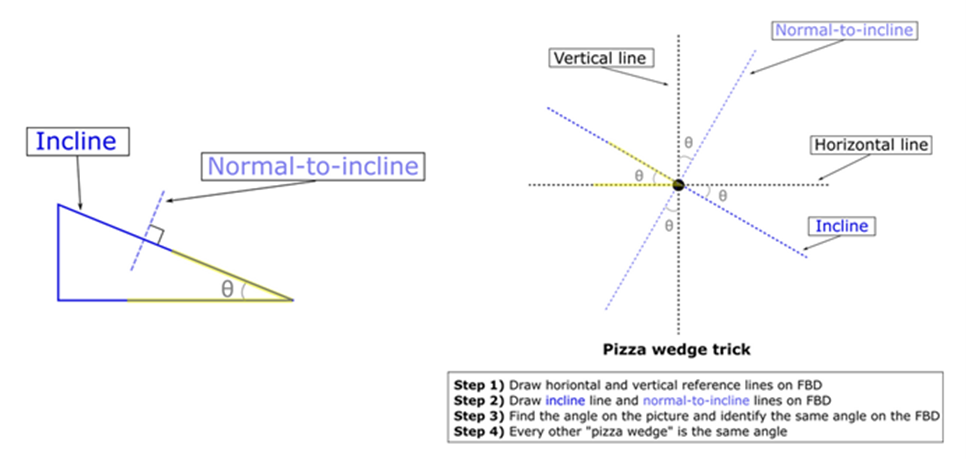
- You still want to align your sum of forces to point in the direction of acceleration, which is usually pointing down or up the inclined plane (and acceleration is usually 0 perpendicular to the plane), so generally speaking you'll usually tilt your axes the same angle that the inclined plane is at, expect in a few notable cases where acceleration is NOT along these axes (uniform circular motion has some instances of this that will come later!).
Multiple Representations
Multiple Representations is the concept that a physical phenomena can be expressed in different ways.
Physical
Mathematical
The main mathematical representation for forces will be applying Newton's Second Law to a physical problem. You will need to analyze the motion of an object and create a free body diagram of the relative forces in order to derive the force equations. We learned in the kinematics section how to analyze motion without any concern about the forces that caused the motion. The infographic below describes the relationship between force and acceleration. Thus, we may now analyze the forces acting on an object to determine the relative acceleration.

Graphical
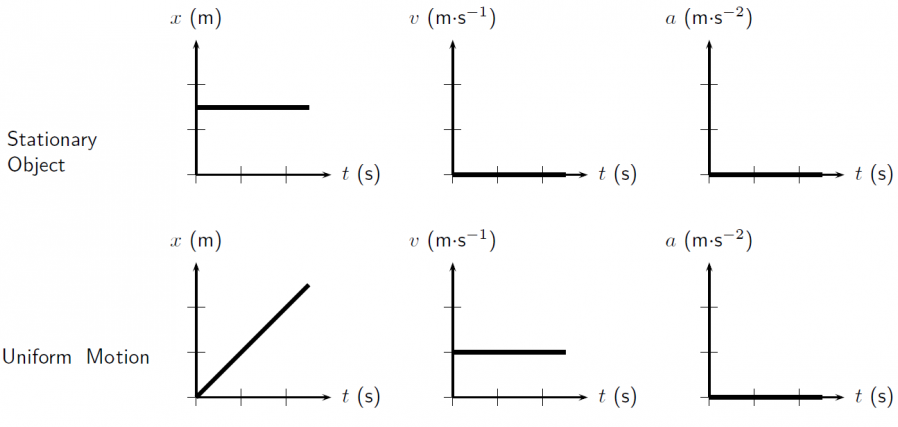 .
.
Descriptive
A spaceship, deep in space, has ran out of fuel. Since nothing is there to act on the ship, it will continue to move at the speed it is moving and in the direction it is moving. It will do this until something acts on it, something like the pull from a nearby star that becomes no longer negligible as the ship passes near the star.
Experimental