F-IP-1 Consider the object on an inclined plane shown below: Fkso is the frictional force exerted on it by the plane, Fnso the normal force exerted on it by the plane, and Fgeo the force of gravity exerted on it by the Earth. Which of the following statements are true regarding this situation?

- Fkso = µ Fnso
- Fkso = Fgeo sin θ
- Fnso = Fgeo cos θ
- The object is sliding up the incline
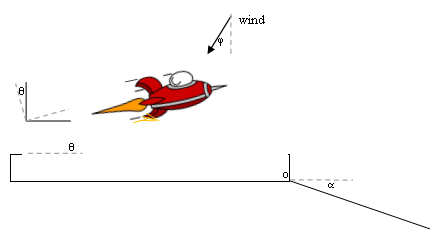
F-IP-2 While starting to take off a rocket ship of mass m malfunctions horribly, leaving the antigravity drive turned off and the throttle stuck with a constant thrust of magnitude Fth. Making matters worse, it’s on a hill angled θ with respect to the horizontal to a cliff of height h above ground. Below the cliff the ground is angled downward α with respect to the horizontal. The coefficient of static and kinetic friction between the rocket and the hill is µs and µk respectively. A steady wind is pushing downward on the ship with a magnitude Fw force at an angle of φ with respect to the vertical. What minimum magnitude thrust would be required for the ship to accelerate up the hill?
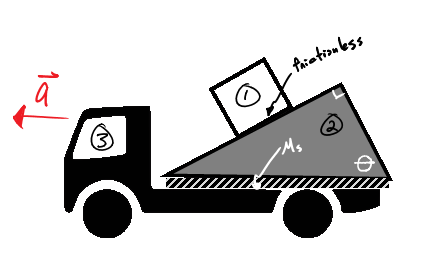
F-IP-3 A square block (m1) sits atop a triangular wedge (m2) that sits on the horizontal bed of a truck (m3). One of the angles of the wedge is θ, as shown in the figure. There is no friction between the wedge and the block but there is friction (µs) between the truck and the wedge. When the truck accelerates as much as it can (amax) and not have the wedge + block system slide relative to the truck, it is noticed that the block does not slide relative to the wedge. (a) For this max acceleration situation draw a free-body diagram for the square, wedge, and truck separately. (b) Identify all Newton’s third law force pairs. (c) When analyzing these objects what coordinate system orientation would best be suited? Explain. (d) Create a set of Newton’s 2nd law equations for each mass using the variables given, and g, the acceleration of gravity. Identify any quantities that are zero. (you do not have to solve for anything) (e) Identify any constraints these objects may have with respect to each other.