Field Theory

A field is a map. It tells you how navigating a region of space may go before you even get there. Imagine a room being warmed by a fireplace in the corner. I could walk to every point in the room, staring with position $\overrightarrow{r}=<0,0,0> m$, and record the temperature in a data table. That table represents the temperature field of the room. That scalar field could then be used to deduce heat transfers in the room. Fields are maps, where every point in space there is information (usually a scalar or a vector), that can be used to explain interactions. Fields are constructs, more than any other we've encountered. They are not observable in any conventional way but are rather a conceptual tool for the study of interactions.

An example of a vector field is a velocity field. Instead of every point in space containing one number, like in the temperature field example, every point in space contains three numbers which are the x, y, and z components of the velocity. A stream that narrows could possibly be described by the velocity field below.

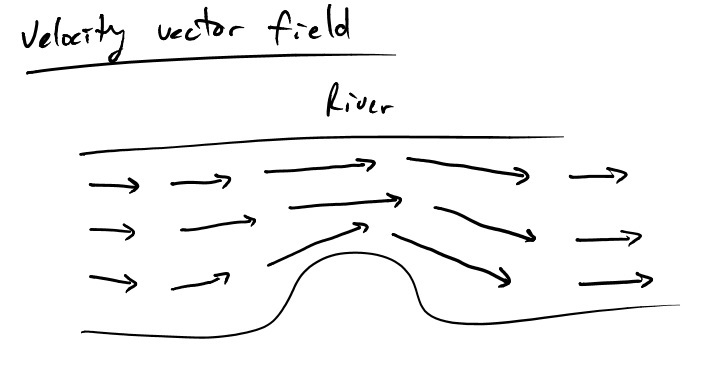
Even though there are not vectors drawn everywhere in the stream does not mean the field is zero at those points, its merely due to the limitation of how many vectors are feasible (and useful) to draw. Now a rubber ducky floating down the river could have a somewhat predictable interaction with the river. It would speed up in the narrow region and possibly change directions if it entered from the bottom. Be careful, the temperature and velocity field examples are not the same as the electric field and potential. They are only used to get a loose feel for the concept.

The Electric Field

All charges create electric fields. We say the charge alters the space around it but this not true in any real way, that is what mass does. Charges rather create a field that can travel through the vacuum of space and influence other charges to feel a force. Consider the situation below where $Q$ is a positive charge that generates the vector field shown. That is the field owned by charge $Q$.

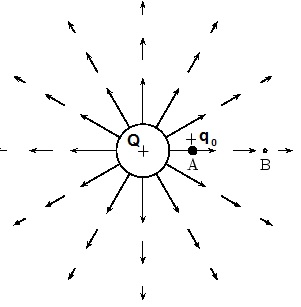
A second charge $q_0$, whose field is not being shown, resides in $Q's$ field. We call $q_0$ the test charge since we are not considering the field it creates. If the electric field from $Q$ is considered to be $\overrightarrow{E}$, then the force that field puts on the test charge follows the following equation.

Force on a Test Charge ($q_0$) in an Electric Field ($\overrightarrow{E}$)

$\overrightarrow{F_0}=q_0 \overrightarrow{E}$

The essence of an electric field lies in this example. The charge $Q$ generates a field that a second charge $q_0$ feels a force from and in that way they interact. This model gives $Q$ ownership to something that can exist without the presence of the second charge. After all, there would be no such thing as a Coulomb force if the second charge didn't exist. It is this reason some consider the electric field to be more fundamental and elegant than Coulombs Law.

Point Charge

The electric field for a point charges points away from positive charges and towards negative charges. It's magnitude has an inverse square dependency on the distance from the charge. If you double your distance from the charge the field decreases by a factor of 4. All of this information is contained in the expression below.

Electric Field for a Point Charge

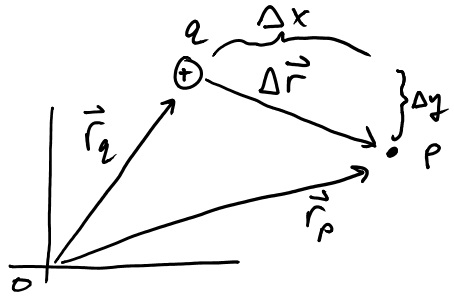                    $\overrightarrow{E}_q(\overrightarrow{r}_p) = \frac{kq}{|\Delta \overrightarrow{r}|^2}\Delta \hat{r}$ 

The above equation reads that the electric field from charge $q$, at point $p$, is equal to a constant ($k=8.99 x 10^9 N m^2/C^2$) times the charge, divided by the square of the absolute value of the change in position from $q$ to $p$, multipled by the delta $r$ hat direction. The $\Delta \hat{r}$ is a unit vector, meaning it has magnitude of 1 and only provides a direction.

$\Delta \overrightarrow{r} = <\Delta{x}, \Delta{y}, \Delta{z}>$

$\Delta \hat{r} = < \frac{\Delta x}{|\Delta \overrightarrow{r}|}, \frac{\Delta y}{|\Delta \overrightarrow{r}|}, \frac{\Delta z}{|\Delta \overrightarrow{r}|}>$

Charge Distribution Field Patterns

The electric field from a distribution of charge, like that on a charged rod, is fundamentally a superposition of all the fields from the individual charges. Electric fields add by the principle of superposition, which is to say they add linearly and like all other vectors we've learned about.

                   $\overrightarrow{E}_{net} = \sum \overrightarrow{E}_i$

Sometimes the physics representation of a field is presented in the form of Field Lines, where the strength of the field is larger where the lines are more closely spaced. In the field line representation, field lines start at positive charges and end on negative charges. The diagram below is the eletric field for a dipole.

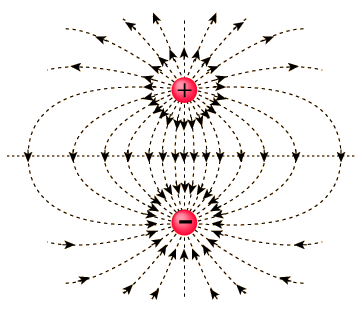
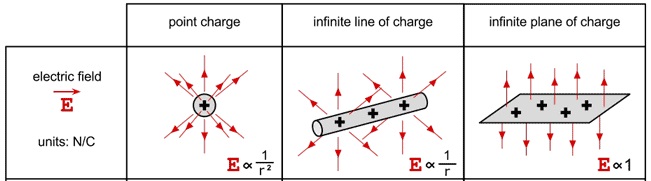
Through superposition, the net field for a number of charge distributions can be determined. It's interesting to note that the electric field for a zero dimensional charge (a point charge) falls off like 1/r² - the field for a one dimensional line of charge falls off like 1/r - and the field from a two dimensional sheet of charge doesn't fall off at all. It's no coincidence that as you increase the dimensions of the charge distribution, the field decreases how fast it falls off.

The Electric Field due to an Infinite Sheet of Total Charge $Q$

$|\overrightarrow{E}_{net}| = \frac{Q}{2 \epsilon_0 A}$,      where $\epsilon_{0} = 8.85 x 10^{-12} F \cdot m^{-1}$, and $A$ is the area of the sheet.

If the sheet is infinite or you are close to a finite sheet, the field doesn't even decrease with increased distance. As you move further away from the plate, the electric fields from charges further and further away start to add more constructively, causing the field to remain constant. Putting two plates separated by some distance, with opposite charges, is called a Parallel Plate Capacitor. The fields inside the plates are uniform and provide an excellent tool for studying electric fields. 

Pre-lecture Videos

Watch these videos before doing the pre-lecture assignment. There's a lot of videos here, check the daily learning guide to know which videos are needed for which lecture. We've also broken grouped the links by day, because we're nice people. ** denotes supplemental but suggested

electric field intro (16min)  

electric field intro (16min)  

pendulum charge in a uniform E field (5min)**

pendulum charge in a uniform E field (5min)

q in uniform E-field (7min)   

q in uniform E-field (7min)   

q in uniform E-field, extended with kinematics (18min) **  

q in uniform E-field, extended with kinematics (18min)

 

net E field - vector addition(5min)

net E field - vector addition(5min)

non-uniform E-field - conceptual point q(7min) ** 

non-uniform E-field - conceptual point q(7min)

uniform E-field - infinite plate(6min)

uniform E-field - infinite plate(6min)

 

 

E-field from point charge - algorithm calculation with rHat(11min)

E-field from point charge - algorithm calculation with rHat(11min)

E-field from point charge - simple symbolic example(6min) **

E-field from point charge - simple symbolic example(6min)

E-field from point charge - example(13min)

E-field from point charge - example(13min)

 

E-field from dipole(9min)

E-field from dipole(9min)

E-field from dipole - vector map(3min)

E-field from dipole - vector map(3min)

E-field - vector vs field lines(4min)

E-field - vector vs field lines(4min)

Openstax has three relevant sections covering the electric field, field lines, and conductors and electric fields in static equilibrium

Electric Field: Concept of a Field Revisited	Electric Field Lines: Multiple Charges	Conductors and Electric Fields in Static Equilibrium

Boston University's Page on electric Field is a neat reference with a couple of example problems

PPLATO is a complete resource with a lot of information, and several practice questions per subject. This webpage covers electric charge, the electric field, and electric potential, we've already covered charge, so focus on the electric field, we'll get to electric potential in the next section.

 

 

The Physics Classroom's section on electric fields. 

 

 

Isaac Physics' section on the electric field is a good short resource on the electric field. On this page there are two drop down sections on electric potential, we'll get to those in the next section, so have a look at the Electric Field, Visualizing and adding electric fields and Electric Fields in Conductors sections

 

 

Other Resources

This link will take you to the repository of other content related resources .

 

Pre-Med Academy has a lot of videos about the Electric Field and Force, too many to list here. We really recommend checking out the content repository for this section and check out the rest of their videos Here are just a few on The Electric Field, Electric Field of a Point Charge, and Electric Field of an Infinite Wire.

Youtube: Pre-Med Academy - Electric Fieldof an Infinite Wire

Doc Schuster has a few good videos on the Electric field. 

 

Youtube: Doc Schuster - The Electric Field

 

 

 

Other Resources

This link will take you to the repository of other content related resources .

 

This flashphysics applet lets you create charge distributions from point charges and plot the corresponding electric field.  Try placing test charges in the region of space to watch possible trajectories!

LINK THAT NEED IMAGE

This PhET interactive is a test of skill! place charges to guide a charged hockey puck around obstacles and into the goal

This Puzzle by Duffy will help you connect the charge and the field.

The Puzzle by Duffy is a bit more challenging.

Use this 3D applet by Falstad to visualize the field for various charge distributions.

For additional simulations on this subject, visit the simulations repository.

 

For additional demos involving this subject, visit the demo repository

(1) What is the magnitude of the Electric field at a location $r = 2 \hspace{0.2 cm} nm$ from a point charge with charge $q=10 \hspace{0.2 cm}nC$ that is located at the origin?

(2) Three point charges $q_1 = q_2 = q_3 = 5 \hspace{0.2 cm}nC$ are placed equidistant from each other on the x-axis: $q_1$ is located at $x= -2 \hspace{0.2 cm}nm$, $q_2$ is located at the origin, and $q_3$ is located at $x = 2 \hspace{0.2 cm} nm$. A point charge $q_4 = 1\hspace{0.2 cm} nC$ is placed on the y-axis, 2 namometers up from the origin. (a) What is the magnitude of the electric force that $q_4$ feels? (b) What is the direction of the electric force on $q_4$? (c) What is the direction of the electric force if $q_4 = -1 \hspace{0.2 cm}nC$ instead?

(3) A point charge $q_1 = -20 \hspace{0.2 cm}nC$ is located at a position $r_1 = <-3,0> \hspace{0.2 cm}nm$. (a) What is the magnitude of the electric field at point $r_a = <0, 3> \hspace{0.2 cm}nm$. (b) By what factor does the magnitude of the electric field at point $r_a$ decrease if another point charge with magnitude $q_2 = 20 \hspace{0.2 cm}nC$ is placed at the origin? (c) Calculate the magnitude and direction of the force that a point charge with magnitude $q_3 = -1 \hspace{0.2 cm}nC$ would feel if it were placed at position $r_a$ for both cases (a) and (b). [Optional (d) What is the electric force on $q_3$ if charge $q_1$ is removed?]

(4) (More time-consuming - practice with computing the electric field from multiple source charges in an arbitrary configuration) Three point charges $q_1 = 5 \hspace{0.2 cm}nC$, $q_2 = 10 \hspace{0.2 cm}nC$, and $q_3 = -2 \hspace{0.2 cm}nC$ are placed as follows: $q_1$ is located at $r_1 = <- 3,0> \hspace{0.2 cm}nm$, $q_2$ is located at $r_2 = <0,0> \hspace{0.2 cm}nm$, and $q_3$ is located at $r_3 = <1, 2> \hspace{0.2 cm}nm$. (a) What is the magnitude and direction of the electric field at point $r_p = <8, 8> \hspace{0.2 cm}nm? 

 

Solutions found HERE

Short foundation building questions, often used as clicker questions, can be found in the clicker questions repository for this subject.

---

 

BoxSand practice problems - Answers

BoxSand's multiple select problems

BoxSand's quantitative problems

Recommended example practice problems 

• *OpenStax, has practice problems at the end of every section
  • Electric Field: Concept of a Field Revisited, Website Link
  • Electric Field Lines, Website Link
  • Conductors and Electric Fields, Website Link
• PhysicsClassroom, 27 problems on charge and the electric field, Website Link
• University of Greenbay: Guided problem on the electric force, Website Link

For additional practice problems and worked examples, visit the link below. If you've found example problems that you've used please help us out and submit them to the student contributed content section.