Check out the field patterns displayed in this video.
Pre-lecture Study Resources
Watch the pre-lecture videos and read through the OpenStax text before doing the pre-lecture homework or attending class.
BoxSand Introduction
Electic Field | Field Patterns
Charge Distribution Field Patterns
The electric field from a distribution of charge, like that on a charged rod, is fundamentally a superposition of all the fields from the individual charges. Electric fields add by the principle of superposition, which is to say they add linearly and like all other vectors we've learned about.
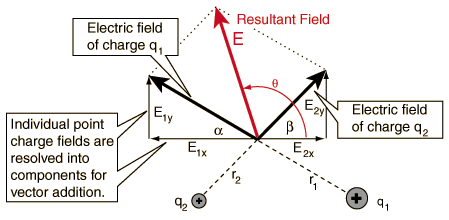 →Enet=∑→Ei
→Enet=∑→Ei
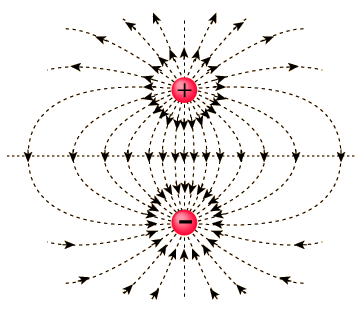
Sometimes the physics representation of a field is presented in the form of Field Lines, where the strength of the field is larger where the lines are more closely spaced. In the field line representation, field lines start at positive charges and end on negative charges. The diagram below is the eletric field for a dipole.
Through superposition, the net field for a number of charge distributions can be determined. It's interesting to note that the electric field for a zero dimensional charge (a point charge) falls off like 1/r2 - the field for a one dimensional line of charge falls off like 1/r - and the field from a two dimensional sheet of charge doesn't fall off at all. It's no coincidence that as you increase the dimensions of the charge distribution, the field decreases how fast it falls off.
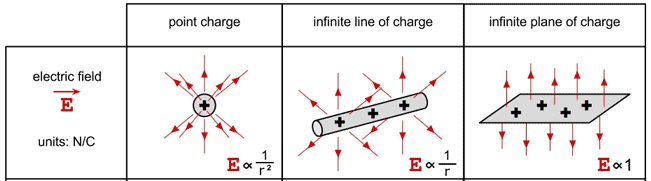
The Electric Field due to an Infinite Sheet of Total Charge Q
|→Enet|=Q2ϵ0A, where ϵ0=8.85x10−12F⋅m−1, and A is the area of the sheet.
If the sheet is infinite or you are close to a finite sheet, the field doesn't even decrease with increased distance. As you move further away from the plate, the electric fields from charges further and further away start to add more constructively, causing the field to remain constant. Putting two plates separated by some distance, with opposite charges, is called a Parallel Plate Capacitor. The fields inside the plates are uniform and provide an excellent tool for studying electric fields.
Key Equations and Infographics



Now, take a look at the pre-lecture reading and videos below.
BoxSand Videos
Required Videos
Suggested Supplemental Videos
none
OpenStax Reading
OpenStax Section 18.7 | Conductors and Electric Fields in Static Equilibrium
OpenStax Section 18.8 | Applications of Electrostatics
Fundamental examples
(1) What is the magnitude of the Electric field at a location r=2nm from a point charge with charge q=10nC that is located at the origin?
(2) Three point charges q1=q2=q3=5nC are placed equidistant from each other on the x-axis: q1 is located at x=−2nm, q2 is located at the origin, and q3 is located at x=2nm. A point charge q4=1nC is placed on the y-axis, 2 namometers up from the origin. (a) What is the magnitude of the electric force that q4 feels? (b) What is the direction of the electric force on q4? (c) What is the direction of the electric force if q4=−1nC instead?
(3) A point charge q1=−20nC is located at a position r1=<−3,0>nm. (a) What is the magnitude of the electric field at point ra=<0,3>nm. (b) By what factor does the magnitude of the electric field at point ra decrease if another point charge with magnitude q2=20nC is placed at the origin? (c) Calculate the magnitude and direction of the force that a point charge with magnitude q3=−1nC would feel if it were placed at position ra for both cases (a) and (b). [Optional (d) What is the electric force on q3 if charge q1 is removed?]
(4) (More time-consuming - practice with computing the electric field from multiple source charges in an arbitrary configuration) Three point charges q1=5nC, q2=10nC, and q3=−2nC are placed as follows: q1 is located at r1=<−3,0>nm, q2 is located at r2=<0,0>nm, and q3 is located at r3=<1,2>nm. (a) What is the magnitude and direction of the electric field at point $r_p = <8, 8> \hspace{0.2 cm}nm?
Solutions found HERE
Short foundation building questions, often used as clicker questions, can be found in the clicker questions repository for this subject.
Post-Lecture Study Resources
Use the supplemental resources below to support your post-lecture study.
Practice Problems
BoxSand practice problems - Answers
BoxSand's multiple select problems
BoxSand's quantitative problems
Recommended example practice problems
- *OpenStax, has practice problems at the end of every section
- Electric Field: Concept of a Field Revisited, Website Link
- Electric Field Lines, Website Link
- Conductors and Electric Fields, Website Link
- PhysicsClassroom, 27 problems on charge and the electric field, Website Link
- University of Greenbay: Guided problem on the electric force, Website Link
For additional practice problems and worked examples, visit the link below. If you've found example problems that you've used please help us out and submit them to the student contributed content section.
Additional Boxsand Study Resources
Additional BoxSand Study Resources
Learning Objectives
Summary
Summary
Atomistic Goals
Students will be able to...
YouTube Videos
Simulations
Demos
Check out the field patterns displayed in this video.
For additional demos involving this subject, visit the demo repository
History
Oh no, we haven't been able to write up a history overview for this topic. If you'd like to contribute, contact the director of BoxSand, KC Walsh (walshke@oregonstate.edu).
Physics Fun
Other Resources
Problem Solving Guide
Use the Tips and Tricks below to support your post-lecture study.
Assumptions
Checklist
Misconceptions & Mistakes
Pro Tips
Multiple Representations
Multiple Representations is the concept that a physical phenomena can be expressed in different ways.
Physical
Mathematical
Graphical
Descriptive
Experimental