Problem Solving Guide
Algorithm
Misconceptions & Mistakes
- Only forces go on a FBD, do not draw velocity or acceleration on a FBD.
- Remember that in addition to contact forces included on a FBD, you must also consider non-contact forces such as gravity.
- One thing people forget when doing a free body diagram is that the choice of axis is not set in stone. This means that every time we draw a FBD we must include the axis that we are using to solve our problem.
- When there are many objects interacting, such as three or four books stacked on each other, many people, when drawing the free body diagram (FBD) for the bottom book, want to draw forces from all of the other books. However, if we draw our system boundary we see that the only book crossing the boundary of the bottom book is the one right above it. The other books do not apply a force directly to the bottom book so we can't include any forces from them on the bottom book.
- Each “separate” system, as we define them, should have a separate FBD that only include forces that act on that specific system. That specific system could contain multiple objects, if they are coupled to one another.
- If there are two systems in the same situation they can still have different axes. Choose the axis that is most advantageous for each system, typically aligning the axis with the acceleration of that particular system. (when relating them be cautious though).
- When summing your forces in a given direction you must sum any force that has even a component in the given direction.
Pro Tips
- If you're struggling to get the forces in the right direction draw them first right on the picture of the system and then move them into a FBD after- maintaining all angles.
- Always start with drawing the angles relative to something easily identifiable in your FBD. If you're struggling draw them from straight vertical or horizontal (at first) you can always define more angles later to make it easier.
- Always draw your FBD before trying to start calculating things. Pick the most useful directions to set your axes and then sum your forces in both directions and set it equal to mass*acceleration (in that direction).
- When possible make the axes such that one of them aligns with the acceleration- this will make your sum of the forces equation easier to solve.
- If you properly scale all of the forces acting on the system, it is way to determine the direction of the net force from a FBD.
- Double check your FBD before you start to translate it into Newton's 2nd law. Make sure you included all contact forces, and non contact forces.
- Do not get x and y axis confused with horizontal and vertical. Often times students will rotate gravity so that it does not point vertically downwards, leading to confusion as to what angles go where.
Multiple Representations
Multiple Representations is the concept that a physical phenomena can be expressed in different ways.
Physical
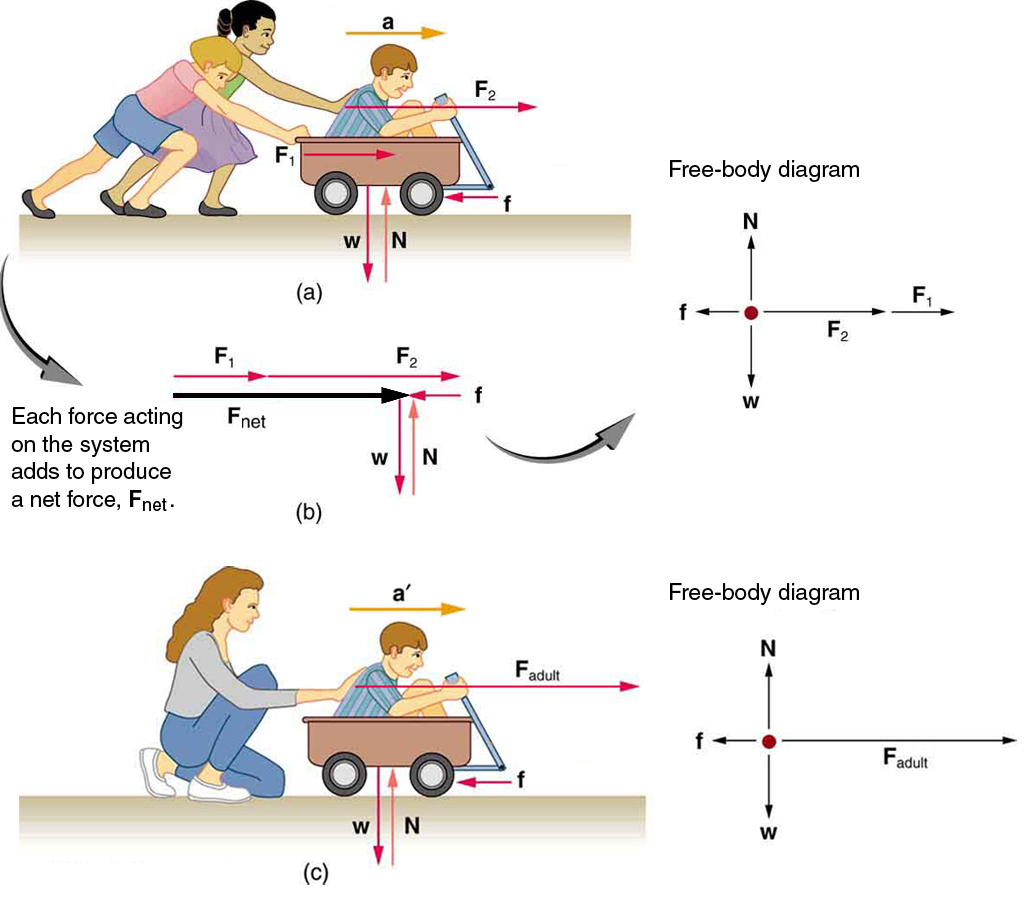

Mathematical
The main mathematical representation for forces will be applying Newton's Second Law to a physical problem. You will need to analyze the motion of an object and create a free body diagram of the relative forces in order to derive the force equations. We learned in the kinematics section how to analyze motion without any concern about the forces that caused the motion. The infographic below describes the relationship between force and accelertion. Thus, we may now analyze the forces acting on an object to determine the relative acceleration.

Page 3 of this site does a wonderful job of showing many of the different mathematical representations.
Graphical
Descriptive
This can be thought of as a word problem. For example, “If Steve pushes a one kilogram box for twelve seconds, and it goes five feet, how hard did Steve push?” would be a descriptive representation of a problem where you would have to translate a FBD into Newton's second law.
Experimental
Here is a video that descibes an actual situation with FBD techniques applied