Problem Solving Guide
Algorithm
Misconceptions & Mistakes
- A big misconception here is confusing mass and weight. Remember mass is how much matter something has, measured in kilograms (kg) whereas weight is the force exerted on something by gravity, measured in Newtons (N). They can be related by weight=mass*gravity (w=mg).
- Although Newton's 2nd law is written in one line, $ \sum \vec{F}=m \vec{a}$, keep in mind this is a vector equation. Thus there are really 3 equations hidden in there, one for each dimension. They are: $ \sum F_x=m \, a_x$, $ \sum F_y=m \, a_y$, $ \sum F_z=m \, a_z$.
- Remember when decomposing force vectors into components, you must go back and put in negative signs by hand based off of your choice of coordinate system.
- Newton's 2nd law equates net force, a vector, to mass*acceleration, a scalar (mass) and a vector (acceleration). Thus if you know the direction of acceleration, then you also know the direction of the net force. The direction of velocity does not determine the direction of the net force.
- Keep in mind that $ \sum \vec{F}=m \vec{a}$ only applies to the total force, so you need to make sure that you are accounting for all forces when setting it equal to mass times acceleration.
Pro Tips
- Do not forget about kinematics!If given information about positions, velocities, and time, you can use Newton's 2nd law to find acceleration, which can be used in kinematic equations.
- Watch your units! Make sure that the answer you get has the units you would expect. Keep everything in SI units.
- If you scale the external forces acting on an object properly, you can graphically add all of the force vectors by drawing them head to tail. This is often useful to be able to quickly determine the direction of the net force.
- Newton's 2nd law deals with vector quantities, thus make sure you always define a coordinate system to account for positive and negative components.
- Look at all the forces on the object and determine which direction the net force would be and use that for $ \sum \vec{F}=m \vec{a}$.
Multiple Representations
Multiple Representations is the concept that a physical phenomena can be expressed in different ways.
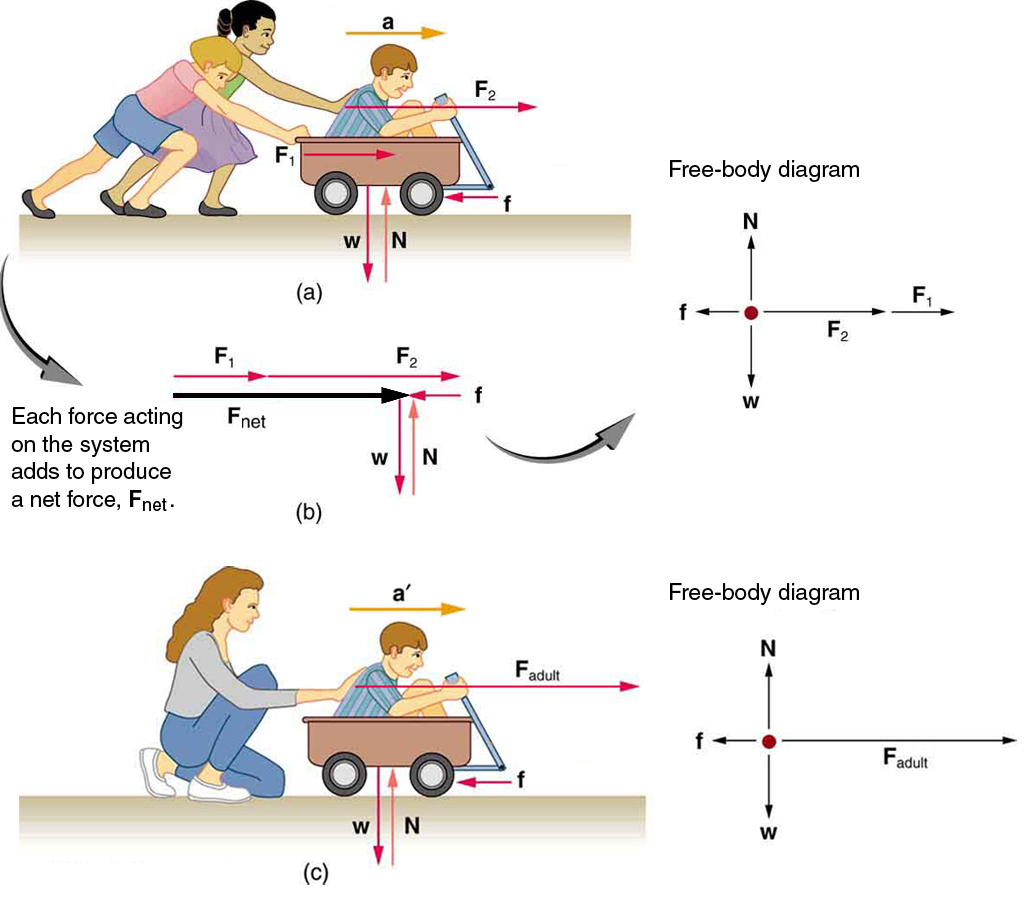
Physical
Mathematical
The main mathematical representation for forces will be applying Newton's Second Law to a physical problem. You will need to analyze the motion of an object and create a free body diagram of the relative forces in order to derive the force equations. We learned in the kinematics section how to analyze motion without any concern about the forces that caused the motion. The infographic below describes the relationship between force and acceleration. Thus, we may now analyze the forces acting on an object to determine the relative acceleration.

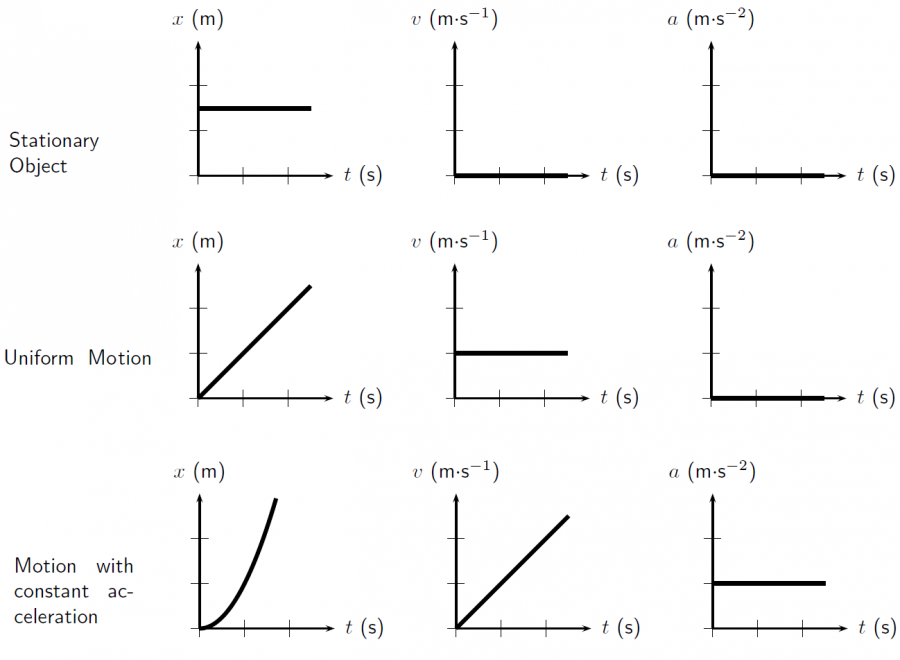
Graphical
Descriptive
A physics student is pushing a $17 \; kg$ crate across a frictionless floor with an acceleration of $0.25 \; m/s^{2}$. What is the relative force the student is applying? We know the mass of the crate, and that the acceleration is a constant $0.25 \; m/s^{2}$. Therefore, we may apply the mathematical representation and determine the relative force the physics student is applying to the crate.
Experimental
We could go out and physically push a $17 \; kg$ crate on a mostly frictionless surface and measure the average distance we travel for some period of time. By measuring the average distanced traveled per unit time, we can determine the acceleration by determining the slope of a velocity versus time graph. This would allow us to use Newton's Second Law and relate the force to acceleration.