We've learned that light slows down as it enters a material with a higher index of refraction. For continuity of the wave, the freqeuncy must remain constant. If $v=f \lambda$, and the frequency is constant but the speed decreases, the wavelength must also decrease.

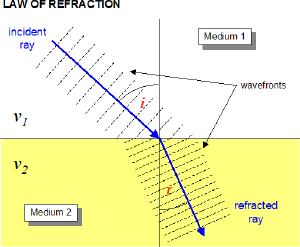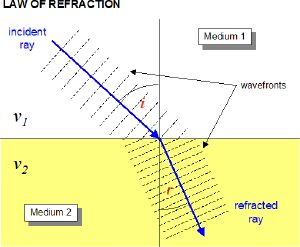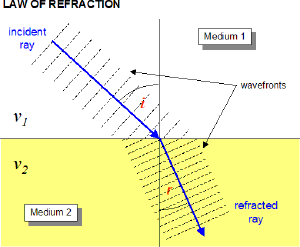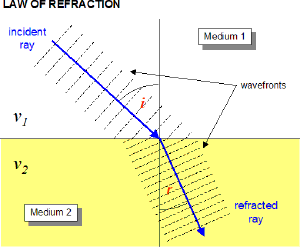
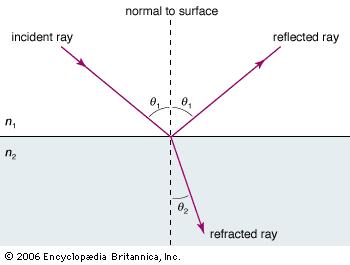
Geometrically the only way for the wavelength to decrease but the wave to remain continuous is if the angle of propagation changes. Snell's law defines the relationship between the incident angle $\theta_1$ and the refracted angle $\theta_2$.

*NOTE: All angles are measured with respect to the normal to the surface.*

$n_1 \sin{\theta_1} = n_2 \sin{\theta_2}$

With this relationship if light travels into a medium with a higher index of refraction, like from air into water, then $\theta_1>\theta_2$ and the light bends towards the normal. If the light instead traveled in the opposite direction, so from a higher to a lower index of refraction, the light would bend away from the normal.

Total Internal Refraction (TIR)

In the right geometery, with the right relationship of index of refraction, light can actually be forced to stay within a medium and not be refracted at all. Imagine traveling from a lower to higher index material.

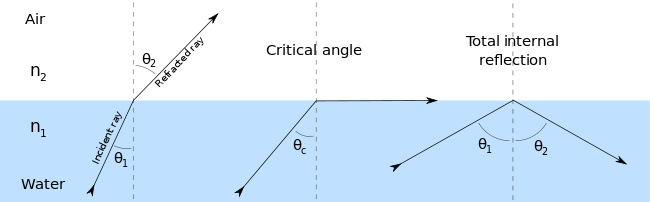
The refracted angle will always be larger than the incident. As $\theta_1$ increases and approaches 90º, $\theta_2$ will reach 90º before $\theta_1$ does. At the critical angle ($\theta_c$), the refracted angle is 90° and $\sin(90)=1$, so all the light is reflected and none of it is refracted.

if $n_1>n_2$,     $\sin(\theta_{c}) = \frac{n_1}{n_2}$

Fiber optics, HAM radio waves that travel around the Earth, and Lightboards work on the principle of Total Internal Refraction.

 Pre-lecture Videos: Watch these videos before doing the pre-lecture assignment, ** denotes supplemental but suggested

Ray model - Snells law (10min)

Ray model - Snells law (10min)

Total Internal Reflection (LB)(9min)

Total Internal Reflection (LB)(9min)

Apparent depth (7min)

Apparent depth (7min)

Dispersion (6min)

Dispersion (6min)

(old version) Total Internal Reflection (5min)

Total Internal Reflection (5min)

 The Openstax text book section 25.3 is a repeat from our introduction to the Index of Refraction . The second half of section 25.3 introduces Snell's Law.

This resource is very direct. Consider looking through it at least once.

The Hyperphysics reference for Snell's Law gives a quick two sentence description with a nice diagram.

Other Resources

This link will take you to the repository of other content related resources .

 Doc Schuster provides a geometric derivation of Snell's Law. This will be a very helpful video.

Here is a quick introduction to Snell's Law

Here is an apparent depth example of Snell's Law

Other Resources

This link will take you to the repository of other content related resources .

Bending of light simulation by PhET to examine Snell's Law.

Here is an easy simulation that looks at Snell's law in an easier form.

One more Snell's law simulation to check out. This one changes the physical direction of the beam for another perspective.

For additional simulations on this subject, visit the simulations repository.

For additional demos involving this subject, visit the demo repository

 (1) Light is traveling through air ($n = 1$) and is incident on a plastic medium at an angle of incidence of $\theta_{inc} = 40 ° $. It enters the plastic medium at an angle of inidence of $\theta_{refr} =  30 °$. What is the index of refraction of the second medium?

(2) Light travels from a medium with index of refraction $n = 2$ into a medium with an index of refraction of $n = 46$. The light crosses the boundary between mediums at an angle of $\theta =30 °$ from the horizontal. What is the angle of refraction?

(3) A piece of glass is floating on a liquid in a beaker that is open to the air. Light is incident on the piece of glass at an angle $60 °$ relative to the normal. The index of refraction of the glass is $n_g = 2.5$ and the index of refraction of the liquid is $n_l = 3$. At what angle relative to the normal does the light enter the liquid?

(4) You are standing above a glass water tank that is 1 meter deep with a red laser pointer, and you aim it down at the tank at a very shallow angle - 80 degrees from the normal. The laser exits the far wall of the tank before it hits the bottom of the tank. The horizontal distance between the laser's entry into the water and its collision with the far wall of the tank is $50$ cm. At what depth does the laser exit the tank? 

Solutions found HERE.

Short foundation building questions, often used as clicker questions, can be found in the clicker questions repository for this subject.

BoxSand practice problems

Conceptual problems

BoxSand's mutiple select problems

BoxSand's quantitative problems

Recommended example practice problems 

• Openstax has practice problems toward the end of each section, Website Link
•  

For additional practice problems and worked examples, visit the link below. If you've found example problems that you've used please help us out and submit them to the student contributed content section.