BoxSand's Resources

Introduction

Superposition of Waves

When two waves enter the same region of space at the same time they interfere in a way that obeys the Superposition of Waves. This addition of waves creates places where the peaks line up and the resultant wave is larger, which would manifest as a bright spot for light waves. There are also regions where the peak from one wave is lined up with the trough from the other and the resultant is wave cancelation, where their amplitudes add to zero and there would be a dark spot. These constructive and destructive areas are seperated by an entire gradient of partially constructive and partially destructive. The resulting interference pattern is one of the defining features of a wave.

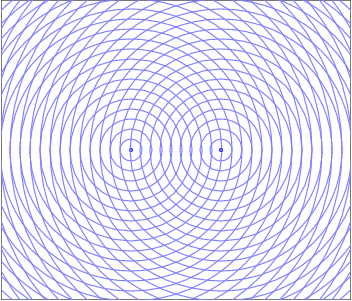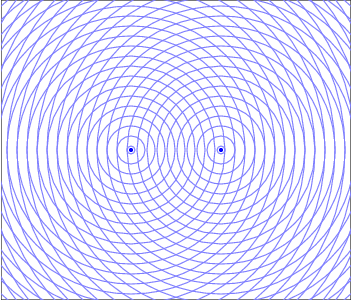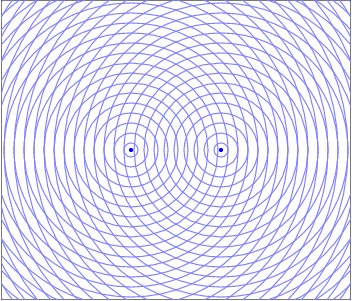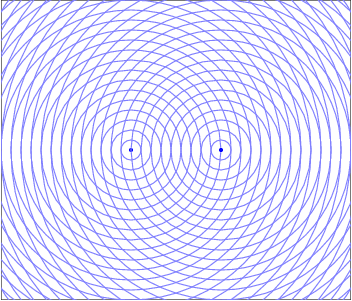
This is a gif of two sources at some distance from each other emitting same frequency. The frequency is shown as circles emitted from the source and there are areas of overlap from the other source.

To learn more about general two source interference, visit the fundamentals of Superposition of Waves.

Wave Interpretation of Light - Young's Double Slit Interference

The theory of Electromagnetic Radiation Wave Theory is one of the most tested and confirmed theories in physics. It relies heavily on the experimental fact that light has wave-like properties. These wave-like properties are displayed by the interference effects that has only been observed in wave systems. The hallmark experiment that enabled us to observe the effect was Young's Double Slit Experiement.

To observe the interference of two sources you need two, coherent, single frequency sources. Essentially you would like two identical sources. The clever way Young achieved this was by isolating a single color of light then sending that light through two small slits. Each slit acts like a new wave source due to the diffraction of light, which is the effect that light "bends" around corners and spreads out when passing through an opening. Since each slit acts like a new source, and each originated from the same source, they are two coherent, single frequency (same color) sources. The diagram below shows a snapshot of the waves as they interfere.

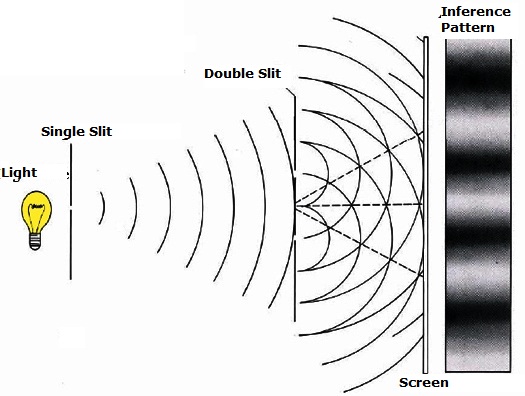
This is an image of a light behind a wall with a single slit. The light emitted then goes through another wall with two slits some vertical distance between each other. The waves emitted from the two different slits have some interference with one another and show an interference pattern with bands of white light and bands of no light.

The modern technology of a LASER (Light Amplification through the Stimulation of Electromagnetic Radiation) has made this experiment much easier due to the very high intensity soures they provide. The experiment also enables one to measure the wavelength of visable light, something on the order of hundreds of nanometers, a size only an order of magnitude greater than the size of atoms. For nearly 100 years this was the only way to probe scales this size scale and it still remains as one of the best.

The geometry of Young's Double Slit is below.

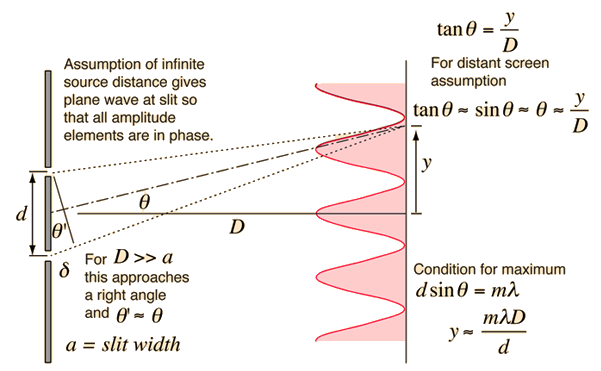
This is an image of a thin wall with two slits with some vertical distance between each other denoted by d and each slit has some width denoted by a. From the top slit there is a line that goes at some angle from the lower vertical labeled as theta prime. From the center of d is another dashed line that is at some angle theta from the horizontal that ends at the center of no light and there is a horizontal distance D to the back wall from the slits. If there was a light shined on the other side of the slit wall, there would be band of light and no light and the distance between the areas of no light are denoted by y. There are notes that says the an assumption of infinite source distance gives plane wave at the slit so that all amplitude elements are in phase. And, for when the distance between the two slits and the back wall is much greater than the width of the slit, this approaches the right angle and theta prime is approximately equal to theta. And, tangent of theta is equal to the distance between the the areas of no light divided by the horizontal distance, for distance screen assumption, this is approximately equal to sine theta which is approximately equal to theta. And, for a maximum condition, the vertical distance between the slits multiplied by sine theta is equal to m multiplied by lambda.

Here the dstance between the slits is $d$ and the screen observing the interference effect is a distance $D$ away from the slits. The central maximum is located along the perpendicular bisector between the two sources where the Path Length Difference (PLD) between the two sources is zero. The condition for constructive interference is for the PLD to be an interger ($m$) multiple of the wavelength. So as you move away from the central maximum and go from constructive to destructive and back to constructive, you've increased the PLD by one whole wavelength. These bright spots are called interference fringes. Using the condition for constructive interference $PLD = m \lambda$ and the geometery that $PLD=d sin(\theta)$, you arrive at the overall condition for constructive interference.

$d sin{\theta}=m \lambda$

The distance $y$ is measured from the central maximum and can be related to the angle ($\theta$) and the distance $D$ by the equation $tan (\theta) = \frac{y}{D}$. In most cases, where $\lambda << d$ the angle is so small that $sin (\theta) \approx \theta$. Since $tan (\theta) = \frac{sin(\theta)}{\cos(\theta)}$ and $\cos(\theta) \approx 1$ for very small angles, $tan(\theta) \approx sin(\theta) \approx \theta$. This allows a more simple connection between the variables shown in the equation below, but note, this only if the angles are very small.

$y \approx \frac{m \lambda D}{d}$,   if $\lambda << d$

Multi-Slit Interference

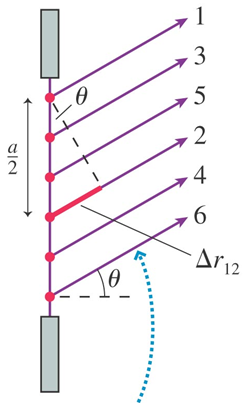
A preferred experiment to measure the wavelength of light is the multi-slit experiment. Instead of only two openings, you have multiple slits, which has the effect of sharpening the constructive interference peaks. The multi-slit apparatus is called a diffraction grating when light passes through it and a reflection grating when light reflects off of it. Below is a diagram for a diffraction grating.

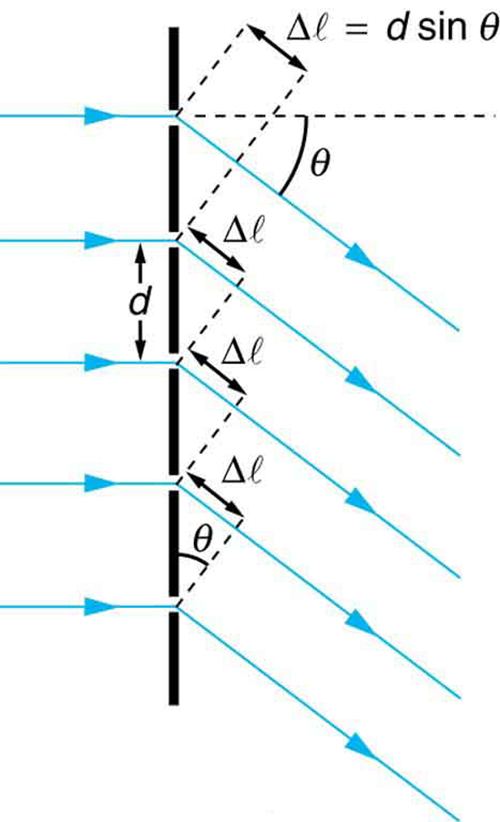
This is an image of a wall with multiple slits of equal vertical distance between each other denoted as d. There are rays of light that enter the slit parallel to one another and are shifted downward at some angle theta from the horizontal. There are dashed perpendicular lines that go up from the point of entry of the light rays and the distance between the dashed lines are labeled as delta l where delta l is equal to d sine theta.

Here the first slit interferes with the second and the second with the third, and so on. Each subsequent slit has the same PLD condition as for a double slit. It is a bunch of double slits slightly shifted from each other. The result is a sharper set of interfrence fringes and the same conditions and equations as for the double slit.

Single Slit Interference

Once you have a wave picture of light and understand superposition, the inteference patterns of the double slit and muti-slit setups are not wierd. But what's truely a mind bender is when passing light through a single slit you also observe an interference pattern, although one different from the double slit. To understand this effect you must consider Huygens Principle which states that each point on a wavefront can act as a new spherical source (left figure).

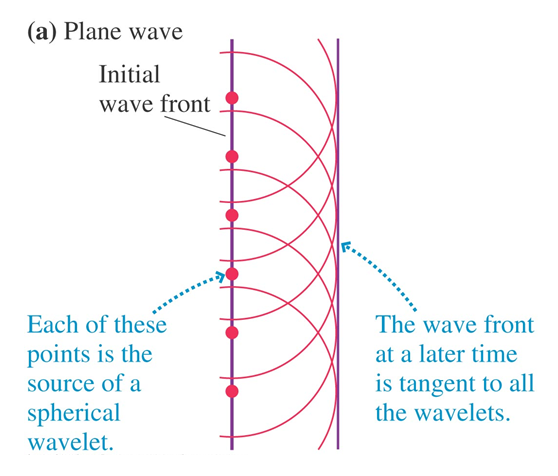
This is an image of a plane wave where there multiple sources that are all lined up vertically which is labeled as the initial wave front. As the source emits light or sound, it moves outwards in a spherical shape where the radius of the circle are all equal. At the edge of the circle, the wave front at a later time is tangent to all the wavelets.            This is an image of a plane wave where there are multiple sources all lined up vertically and are connected to a wall on either side. The distance between the wall and the center source is labeled as a divided by two and each source emits some light at some angle to the horizontal in parallel lines. There are six lines total that are labeled from top to bottom as one, three, five, two, four, six. At the same angle theta from the vertical on source one, the point at which it meets line two and the distance between the source of two to that intersection is labeled as theta r of one and two.

Each new spherical source interfere to create the next wavefront, which can then be a set of new spherical sources. This may seem counter intuitive and we don't know if light really behaves this way, but if modeling it this way is consistent with observation, we can't throw it out as a possibility. In fact this model then helps us understand the single slit interference pattern. Now waves generated at the top of the source can interfere with waves on the bottom of the source (figure above on the right).     

The interference pattern is similar in that there are light and dark regions but it differs in the locations of the maxima and minima.

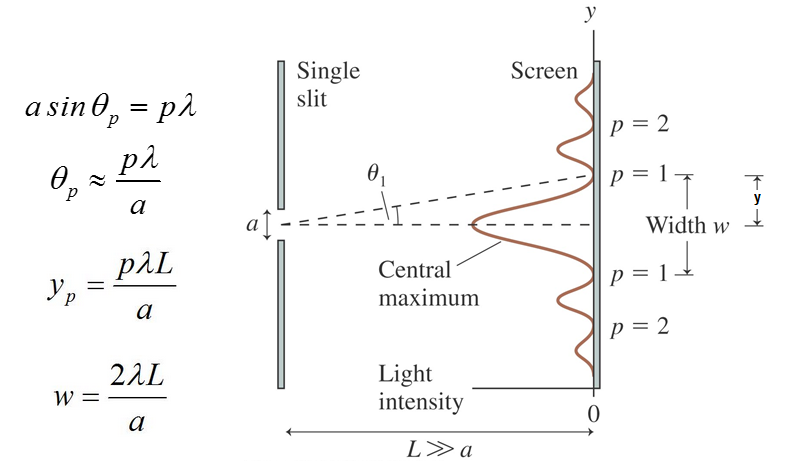
This is an image of a wall with a single slit that has a width of a. The distance between the slit and the second wall is labeled as L from the slit at some angle theta to the first band of no light is labeled as angle theta. On the other wall, there are bands of light with different intensities and bands of no light. The central band of light directly from the slit is the most intense and is called the central maximum. Then there are bands lower in intensity. The distance between the areas of no light is labeled as width w and the adjacent bands of light on either side of the central maximum is labeled as p equals one and the next lower intensity band of light labeled as p equals two. The distance between the central maximum and the area of dark band is labeled as y. On the right shows several equations. The slit width a multiplied by the sine of theta p is equal to p lambda. Theta p is approximately equal to p lambda divided by a with the assumption that the distance between the slit and the screen is much larger than the slit width. Y of p is equal to p lambda multiplied by L all divided by a. W is equal to two lambda multiplied by L all divided by a.

The interference is also often discribed by the locations of the destructive interference points. Here the integer $p$ is describing the order of the dark fringes. The width of the cental maximum ($w$) can be found by doubling $y_1$.

To see the difference between the single and the double slit interference patterns, along with the effects of sharpening the fringes by adding more slits, refer to the figure below.

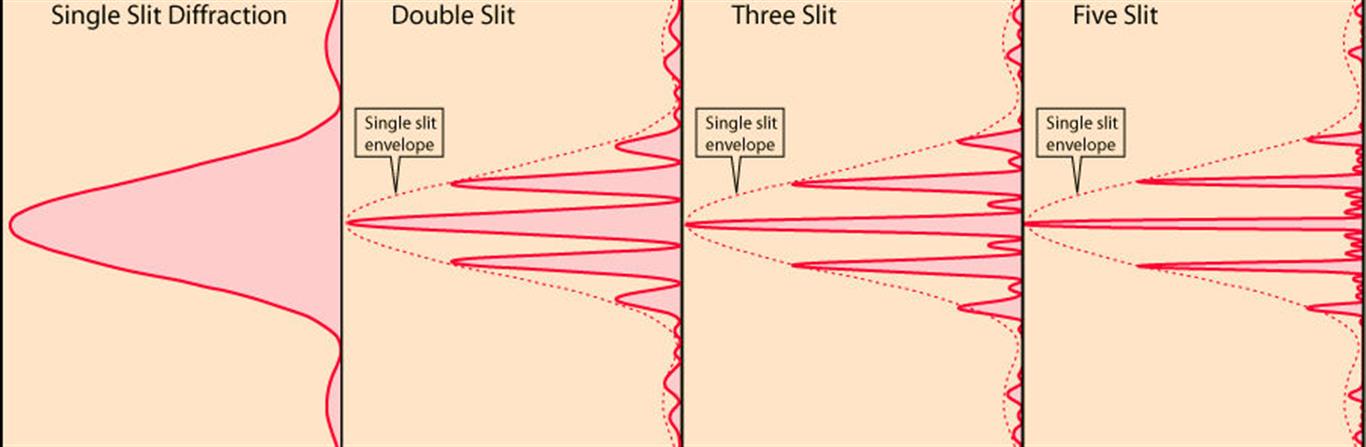
This is an image of four different kinds of slit apparatuses. The first shows a single slit diffraction where there is a very intense central maximum and two faint with lower intensity fringes. The double slit shows the central maximum labeled as the single slit envelope and two slightly lower intense peaks on either side and lower intense fringes. The three slit shows the central maximum labeled as the single slit envelope and two slightly lower intense peaks on either side and even slightly lower intense peaks on either side of those with less intense fringes. The five slit shows the central maximum labeled as the single slit envelope and two slightly lower intense peaks on either side with more fringes on either side. This is to show that with increasing slits, the greater the sharpening of the fringes.

Videos

Pre-lecture Videos: Watch these videos before doing the pre-lecture assignment, ** denotes supplemental but suggested



Review from last term **

Interference review (17min)  **

Interference review (17min) 

Interference example - radar detection (17min) **

Interference example - radar detection (17min)  Youngs Double Slit - Apparatus and conceptual (15min)

Young's Double Slit        

Youngs Double Slit - Apparatus and conceptual (15min)

 

Youngs Double Slit - Apparatus and conceptual (15min)

 

Youngs Double Slit - Apparatus and conceptual review(2min) **

 

Youngs Double Slit - Apparatus and conceptual review(2min) 

 

Youngs Double Slit - governing equations (6min)

 

Youngs Double Slit - governing equations (6min) 

 

Youngs Double Slit - example - simple with small angle (5min) **

 

Youngs Double Slit - example - simple with small angle (5min) 

 

Diffraction and Reflection Gratings

Diffraction Grating - conceptual (6min)

 

Diffraction Grating - conceptual (6min)

 

Reflection Grating - conceptual (4min)

 

Reflection Grating - conceptual (4min)

 

Reflection Grating - simple example - beetle (2min)  **

 

Reflection Grating - simple example - beetle (2min)

 

Spectroscopy and Single Slit Interference

Spectroscopy - conceptual (11min) **

 

Spectroscopy - conceptual (11min)

 

X-Ray Bragg Diffraction - conceptual (7min) **

 

X-Ray Bragg Diffraction - conceptual (7min)

 

Single Slit Diffraction (11min) **

 

Single Slit Diffraction (11min)

 

Single Slit Diffraction - equations(4min)

 

Single Slit Diffraction - equations(4min)

 

Diffraction (4min)

 

Diffraction (4min)

 

Single Slit Diffraction - example (2min) **

 

Single Slit Diffraction - example (2min)

 

Diffraction - circular apperatures (4min) **

 

Diffraction - circular apperatures (4min)

 

Web Resources

Text

 On OpenStax, these 5 short sections, Wave Aspect of Light, Hyugen's Principle, Young's Double Slit Experiment, Single Slit Diffraction, and Double Slit Diffraction contain the information for this section. This link takes you to the first section, Wave Aspect of Light.

Wave Aspect of Light Huygen's Principle: Diffraction Young's Double Slit Experiment
Openstax College Textbook Icon Openstax College Textbook Icon Openstax College Textbook Icon
Multiple Slit Diffraction Single Slit Diffraction
Openstax College Textbook Icon Openstax College Textbook Icon

 

The physics classroom has two relevent sections, The Wavelike Behaviors of Light, and Two Point Source Interference.

The Physics Classroom Icon

Kathy Hadley has a great explaination of the Single Slit interference and Huygens Principle.

Other Content Icon

Hyperphysics usual reference, this time for multi-slit interference. You can get to Single slit and diffraction gratings from the links in the frist box.

Hyper Physics Icon

This is a good, large powerpoint which covers wave interference and diffraction,

P.D.F Icon

 

Other Resources

This link will take you to the repository of other content related resources .

Content Icon

Videos

Doc Schuster covers wave interference,

https://www.youtube.com/watch?v=_N5Y9PVxHLY

Doc Shuster covers single slit diffraction,

https://www.youtube.com/watch?v=ps8IBv5_VeM

Some mathematicas behind double slit diffraction,

https://www.youtube.com/watch?v=KeHry37evb4

Other Resources

This link will take you to the repository of other content related resources .

Content Icon

Simulations

Phet - wave interference, 

Phet Interactive Simulations Icon

For additional simulations on this subject, visit the simulations repository.

Simulation Icon

Demos

For additional demos involving this subject, visit the demo repository

Demos Icon

Practice

Fundamental examples

 

(1) A red laser with wavelength $\lambda = 700$ nm shined on a double-slit with width $d=10$ mm. The screen is located $D= 2 $ m away from the slit. How far up from the central maximum is the $m=2$ bright fringe?

(2) How does the position of the 2nd bright fringe in example 1 change if the wavelength used is $\lambda_{new} = 350$ nm instead of $\lambda_{old} = 700 $ nm?

(3) In a single-slit experiment, the width of the central maximum is $1.5 $ mm. The screen is 1 meter from the slit and the wavelength of light used in this experiment is $360 $ nm. (a) What is the size of the slit? (b) How much wider would the central maximum be if the wavelength was tripled?

(4) In a single-slit experiment, the second dark fringe is located 7.5 cm from the center of the central maximum on a screen located $L = 3 m$ away from the slit. What is the distance between the second dark fringe and the third dark fringe that is located on the other side of the central maximum? The wavelength of the illuminating light is $\lambda = 600 $ nm.

Solutions found HERE

Short foundation building questions, often used as clicker questions, can be found in the clicker questions repository for this subject.

Clicker Questions Icon

 

Practice Problems

BoxSand Practice Problems

Conceptual Problems

BoxSand's multiple select problems

BoxSand's quantitative problems

Recommended example practice problems 


For additional practice problems and worked examples, visit the link below. If you've found example problems that you've used please help us out and submit them to the student contributed content section.

Example Problems Icon Student Contributed Content Icon

 

Arrow that takes you back to the Overview section Arrow that takes you to the Tips and Tricks section