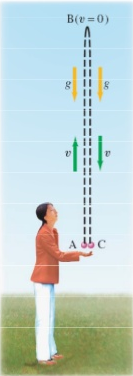
Projectiles are objects launched with both horizontal and vertical components to their velocity. This section takes what was learned in 2D kinematics and helps quantify this movement. Some examples would be a baseball being thrown or a stuntman in a car driving off a cliff.
OpenStax has a rad trailer about projectile motion.
Pre-lecture Study Resources
Read the BoxSand Introduction and watch the pre-lecture videos before doing the pre-lecture homework or attending class. If you have time, or would like more preparation, please read the OpenStax textbook and/or try the fundamental examples provided below.
BoxSand Introduction
2-D Kinematics | Projectile Motion
Projectile motion is a special case of 2D kinematics, where the acceleration is constant and points down towards the Earth. It's free-fall in two dimensions. Since the acceleration points downward, using a standard coordinate system where the x-direction is along the horizontal and the y-direction is along the vertical, means that there is zero x-component to the acceleration. If an object is not accelerating in a given direction, then it maintains a constant speed along that direction, as denoted by the constant length of the $V_x$ component of the velocity vector in the physical representation below.
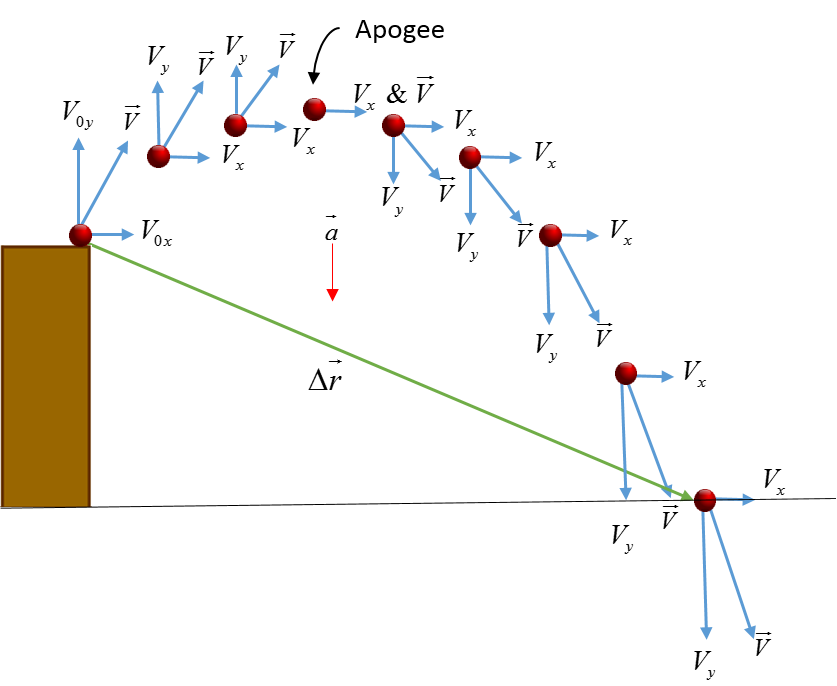
In the physical representation of an object in projectile motion, notice that the x-component of the velocity remains constant, while the y-component does not. The y-component of the velocity decreases on the way up, since $v_y$ points in the opposite direction of $a_y$ and then on the way down the y-component increases, since both $v_y$ and $a_y$ point in the same direction. If air resistance is negligible, the path of the motion is parabolic.
Key Equations and Infographics


BoxSand Videos
Required Videos
Suggested Supplemental Videos
none
OpenStax Reading
Fundamental examples
1. A ball is launched from ground level on a flat surface with a speed of $42 \, m/s$ and at an angle of $30^{\circ}$ with respect to the horizontal.
a. How far does the ball travel before it hits the ground?
b. How long was the ball in the air?
2. A car traveling at a constant $30 \, m/s$ drives off of a level cliff that is $50 \, m$ above level ground.
a. How far from the base of the cliff does the car land?
b. How long was the car in the air?
3. After jumping off a diving board that is $10 \, m$ above water, it is found that the diver lands $3.42 \, m$ away from the base of the diving board with a final velocity of $\langle 1.71 , -14.8 \rangle \, m/s $. What was the divers initial speed and direction when jumping off the diving board?
CLICK HERE for solutions.
Short foundation building questions, often used as clicker questions, can be found in the clicker questions repository for this subject.
Post-Lecture Study Resources
Use the supplemental resources below to support your post-lecture study.
Practice Problems
BoxSand Practice Problems (SOLUTIONS)
BoxSand's Quantitative Practice Problems
BoxSand's Multiple Select Problems
Recommended example practice problems
Set 1: UoW-Greenbay: Range of Baseball. Height of an Arrow,
Set 2: Physics Classroom, set of 8 basic projectile motion problems
For additional practice problems and worked examples, visit the link below. If you've found example problems that you've used please help us out and submit them to the student contributed content section.
Additional Boxsand Study Resources
Additional BoxSand Study Resources
Learning Objectives
Summary
Students will extend what they learned in 1-D kinematics into motion in 2-D and understand the features of perpendicular components. We also want them to learn about the features of projectile motion.
Atomistic Goals
Students will be able to...
- Identify that the motion occurs in more than 1-dimension and requires a 2-D analysis.
- Define a coordinate system that simplifies the complexity of the vector analysis.
- Construct a physical representation the involves multiple dimensions and show a representation of the vector components.
- Demonstrate the ability find the Cartesian components of a vector in the mathematical representation.
- Identify known and unknown quantities for each object, stage, and dimension.
- Solve for a desired unknown in the mathematical representation using a set of kinematic equations for each dimension. Use the problem solving skills developed in 1-D kinematics
- Identify which quantities are the same when comparing two different dimensions, objects, or stages, e.g. elapsed time is the same for both x and y motion.
- Define projectile motion.
- Show that in projectile motion the acceleration has a magnitude of g = 9.8 m/s2 and points downward.
- Show that in projectile motion time of flight is determined in an analysis of the vertical motion.
- Show that in projectile motion the horizontal motion can be the same between two cases even when the vertical is not.
- Show that in projectile motion range depends on both the horizontal speed and the time of flight, thus dependent on both the vertical and horizontal analysis.
- Show that in projectile motion the range is the same for complementary angles.
- Show that in projectile motion any system can be analyzed using only the fundamental kinematics equations for constant acceleration, e.g. you do not need specially derived equations like the range equation.
- Apply limiting cases sense-making procedures to check their solutions.
YouTube Videos
Our good friends at Flippin Physics discuss projectile motion(with an amazing intro sequence)
Projectile launched at an angle by Khan Academy.
Other Resources
This link will take you to the repository of other content related resources.
Simulations
This simulation has several initial conditions that change the trajectory of the object,
For additional simulations on this subject, visit the simulations repository.
Demos
History
Oh no, we haven't been able to write up a history overview for this topic. If you'd like to contribute, contact the director of BoxSand, KC Walsh (walshke@oregonstate.edu).
Physics Fun
Other Resources
Problem Solving Guide
Use the Tips and Tricks below to support your post-lecture study.
Assumptions
- On top of the other assumptions used to preform Kinematics analaysis (see assumptions 2-4), Projectile Motion is a special case where the acceleration in the x-direction is 0 and the the acceleration in the y-direction is g (usually negative g if you're using a standard coordinate system). Remembering that the magnetiude of near Earth acceleration due to gravity (g) is 9.8 m/s^2.
- Kinematics requires the assumption that acceleration is constant, if that isn't true, none of our equations or analysis techniques are necessecarily true for the motion anymore. This is often glossed over, however, as we move onto different types of analysis in the future and have multiple ways to solve problems (like say, on your final exam), the thing to remember about when you can or can't use kinematics is that the acceleration MUST be constant throughout the entire motion if you wish to analyze it with kinematics.
- Motion in one direction, x or y for example, does not imply or interfere with the motion in the other direction, provided those direction are perpindicular to each other (which all the coordinate systems we'll use in this class are).
- The ONLY thing common between the perpindicular directions in 2D kinematics is time, so often that can be used to bridge the gap in information between one direction and another.
Algorithm
1. Read and re-read the whole problem carefully.
2. Visualize the scenario. Mentally try to understand what the object is doing.
a. Motion diagrams are a great tool here for visual cues as to what the motion of an object looks like.
Misconceptions & Mistakes
- Projectile motion is defined as the motion of an object that is only subject to an acceleration due to gravity. This can be either an object dropped from a cliff, or an object thrown off a cliff with an initial speed. If there is any other source of acceleration the object is not in projectile motion, e.g. a rocket while it’s engine is providing thrust.
- An object's acceleration does not determine the direction of motion of the object.
- When an object is thrown upwards at an angle near the surface of the earth, the y-component of velocity is zero at the maximum height that the object reaches, the acceleration is not zero.
- Remember that the velocity in one direction does not imply velocity in another.
- The displacement of an object does not depend on the location of your coordinate system.
- The final velocity of an object when dropped from some height above ground is not zero. The kinematic equations do not know that the ground is there, thus the final velocity is the velocity of the object just before it actually hits the ground.
- Don't confuse acceleration due to gravity with initial velocity.
- Remember that the entire time the acceleration is equal to gravity, no matter which direction the projectile is traveling.
Pro Tips
- Draw a physical representation of the scenario in the problem. Include initial and final velocity vectors, displacement vector, and acceleration vector.
- Place a coordinate system on the physical representation. Location of the origin does not matter, but some locations make the math easier than others (i.e. setting the origin at the initial or final location sets the initial or final position to zero).
- Always identify and write down the knowns and unknowns.
- Be very strict with labeling the kinematic variables; include subscripts indicating which object they are associated with, the coordinate, information about what stage if a multi-stage problem, and initial/final identifications. Doing this early on will help avoid the common mistake of misinterpreting the meanings of the variables when in the stage of algebraically solving the kinematic equations.
- Remember in 2D kinematics problems is that the two dimensions are entirely independent of each other. Treat them separately, come up with the knowns and unknowns for all variables in each direction.
- Keep track of your angles and break all forces in various directions into their components in your chosen coordinate system.
- Always look for the right triangles- using trigonometry effectively is key to solving problems in more than 1D.
- Keep track of the x & y direction's motion separately- have knowns and unknowns for each and set up kinematic equations for each.
- You do not have to break the motion of the projectile into multiple stages so long as the acceleration is constant through the entire motion. For example you typically do not need a stage while it is moving upward and a stage while it is falling downward. Sometimes that may be useful if you need to use the fact that the velocity is zero at the peak of the motion, but in general that is not necessary.
Multiple Representations
Multiple Representations is the concept that a physical phenomena can be expressed in different ways.
Physical
Kinematics problems are often analyzed with physical descriptions. Below we have an object launched from a ledge with initial horizontal and vertical velocity components. The vectors indicate the relative magnitudes of the horizontal and vertical velocity components at different stages of the objects motion.

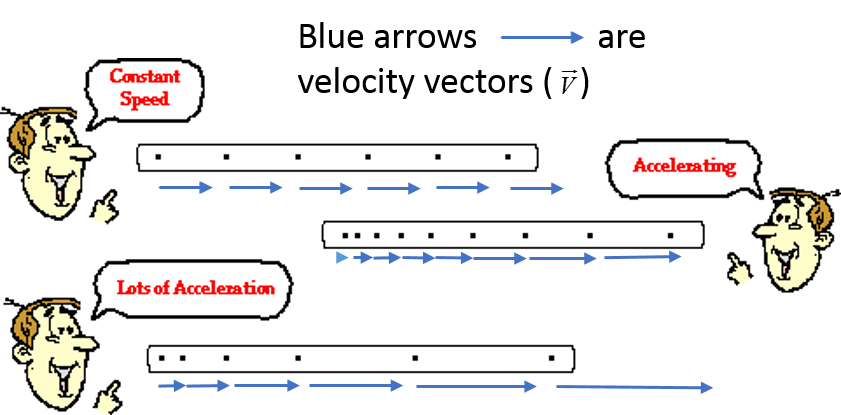
In addition, simple 1D motion diagrams are utilized to describe the speed of an object and whether or not the object has any acceleration.
Mathematical
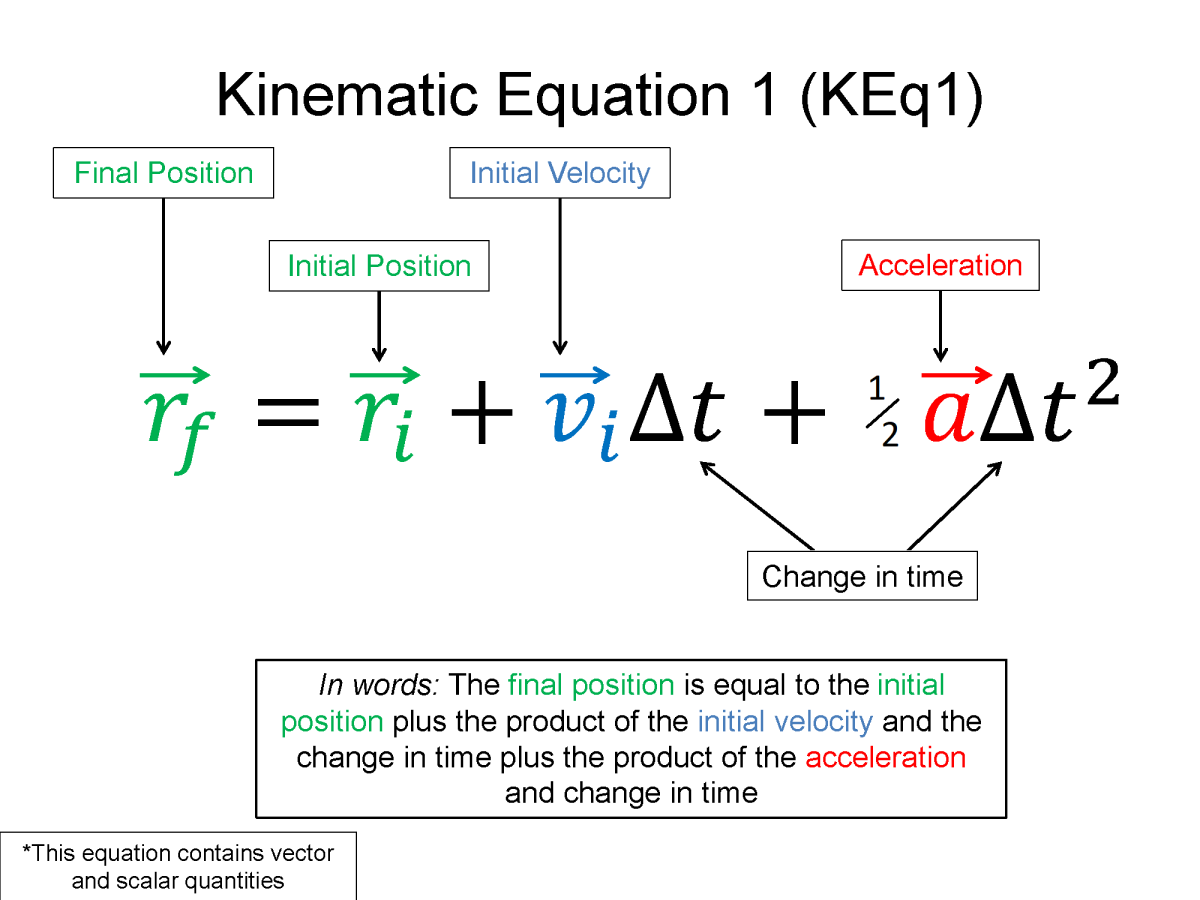
Main kinematics equations. Notice that we use $ r $ to represent the vector position. In the videos below, Professor Matt Anderson uses $ x $ and $ y $ to denote position in a given coordinate direction.
$ \vec{r}_{f} = \vec{r}_{i}+\vec{v}_{i} \Delta t + \frac{1}{2} \vec{a} \Delta t^{2} $
$ \vec{v}_{f} = \vec{v}_{i} + \vec{a} \Delta t $
$ v_{fx}^{2} = v_{ix}^{2}+2a_{x} \Delta x $
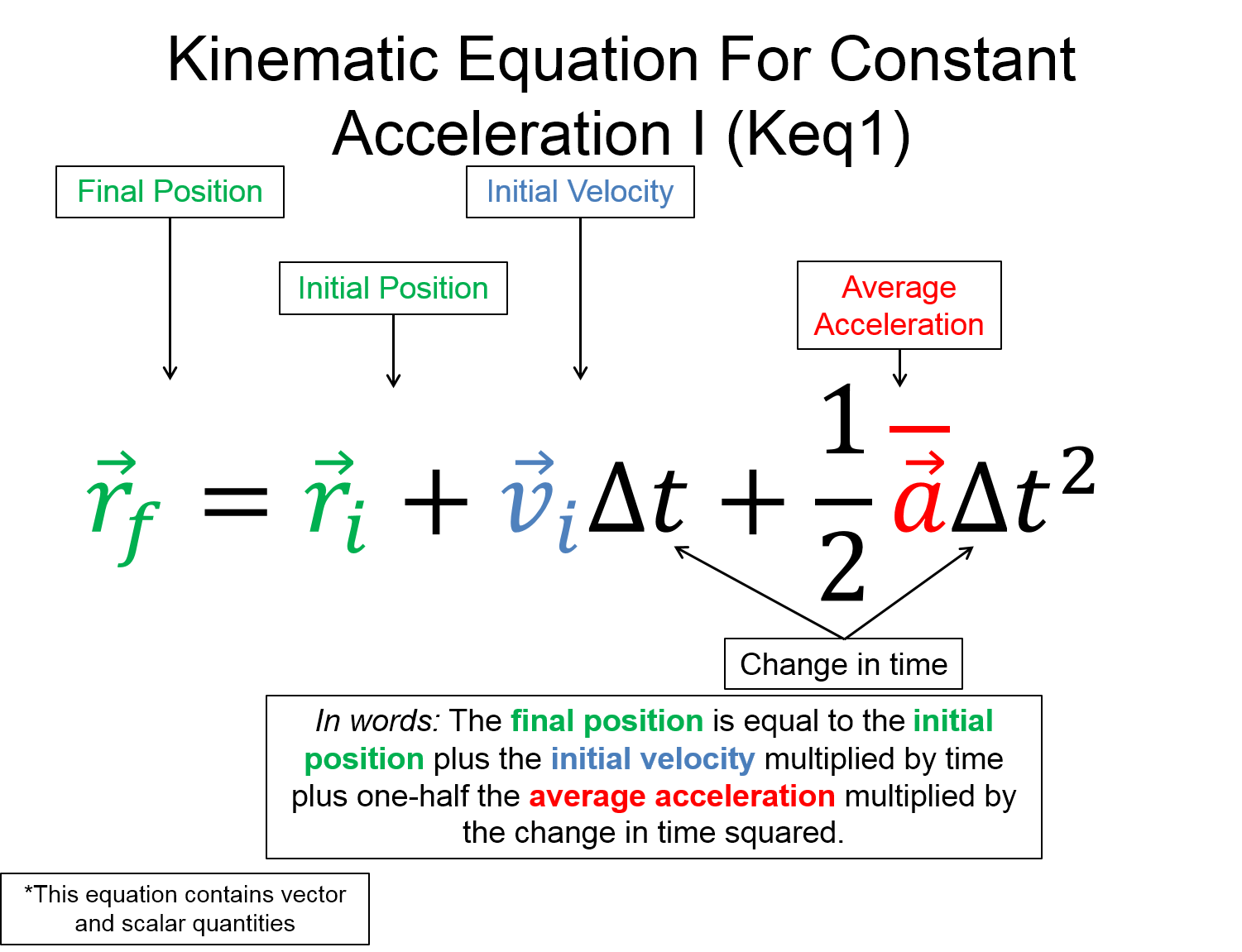

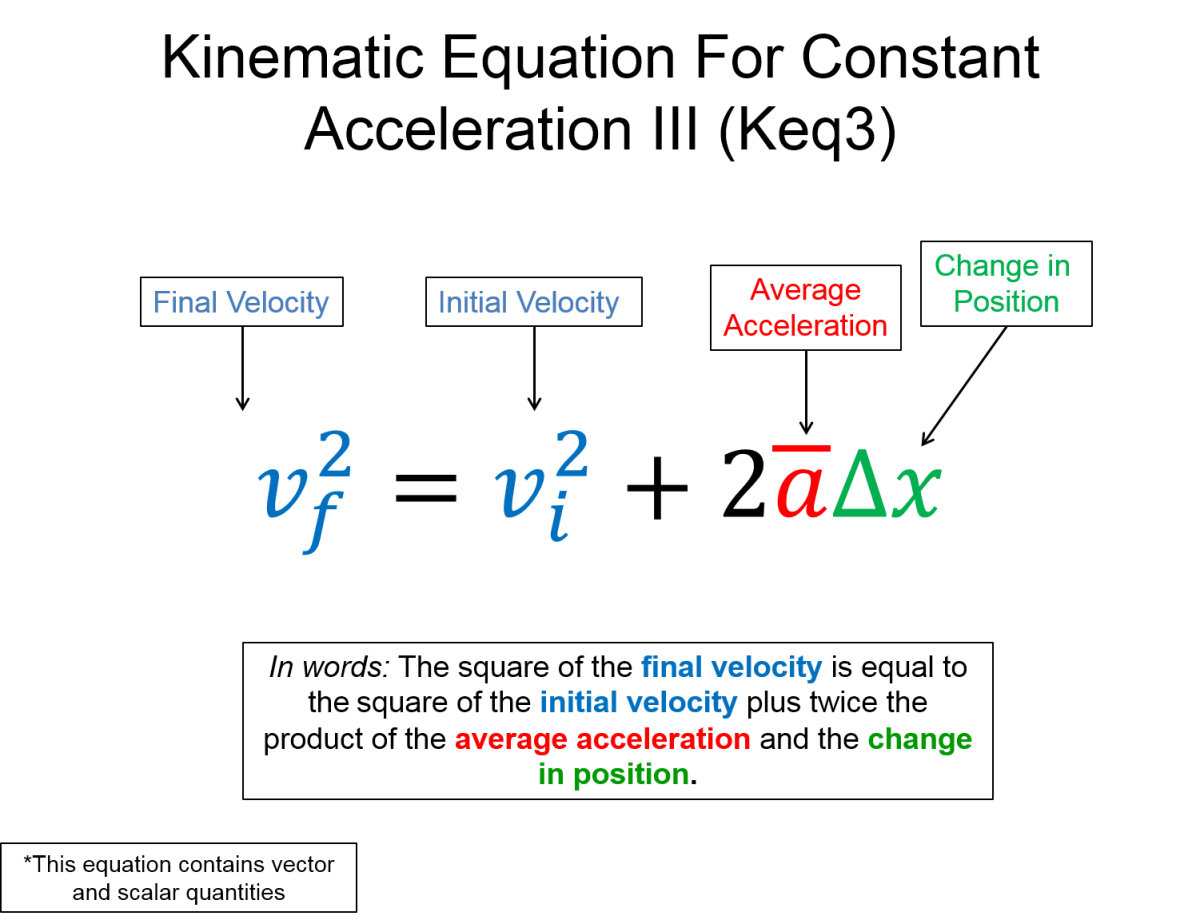
Watch Professor Matt Anderson explain 1D and 2D Kinematics equations using the mathematical representation.
Video 1: Kinematics equations in 1D
Video 2: Kinematics equations in 2D
Graphical
the Physics Classroom introduces the relationship between kinematics equations and their graphical representation. In addition, for a more in-depth discussion please refer to the graphical analysis section.
Descriptive
The branch of mechanics concerned with the motion of objects without reference to the forces that cause the motion.
Experimental
For example, a person throws a ball upward into the air with an initial velocity of $15.0 \frac{m}{s}$. You can calculate how high it goes and how long the ball is in the air before it comes back to your hand. Ignore air resistance.